Making a Maths Question out of a Mole Hill

 

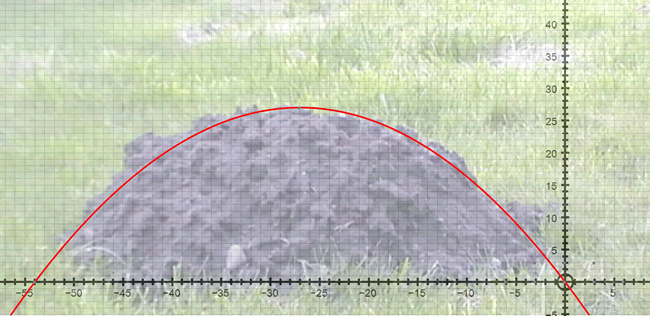
A semi-spherical molehill was found to have a base of diameter 54cm and a perpendicular height of 27 cm.
The earth is considered to be of good quality and will be used to pot some plants.
How many 15cm diameter base cylindrical pots can be filled to a height of 12 cm ?

 

 

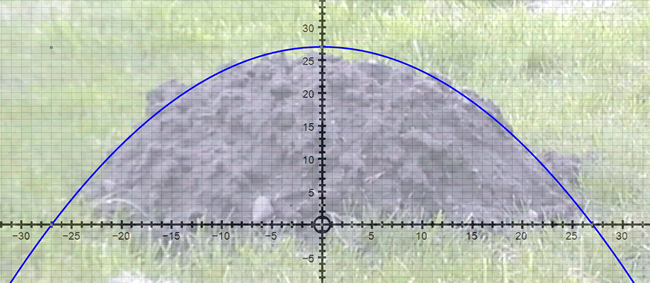
Find an equation which approximately describes the outline of the mole hill.
Is this the only possible answer ? Give reasons to back up your response.

Find the vertical cross sectional area of the mole hill at its highest point.
Find a circle equation which describes the outline of the mole hill.

 

 

Solutions are available further down the page.

 

 

 

↓

 

 

 

 

 

 

 

 

 

 

 

↓

 

 

 

 

 

 

Not yet!

 

 

 

 

 

 

 

 

 

 

 

 

 

↓

 

 

Solutions

The molehill is semi-spherical, so find half of the volume of a sphere with radius 27cm.

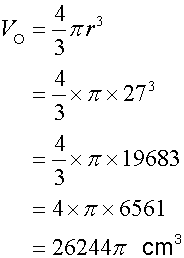
so

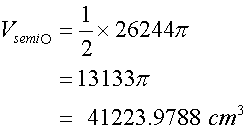
Turning the result into litres;

Giving the volume of earth as 41223.98 cm³ or 41.23 litres.

The cylindrical plant pots have volume

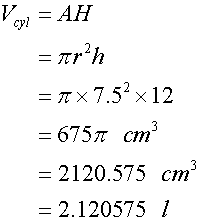
i.e. 2120.58 cm³ or 2.12 litres.

To find the number of plant pots which can be filled, divide the total amount of earth available by the volume of the plant pot.

 

This gives

 

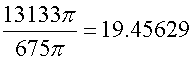
or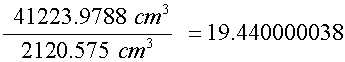

or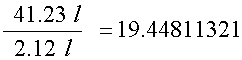

depending on degree of accuracy.

Either way, a total of 19 plant pots can be filled with earth from the molehill.

 

To find the equation of the mole hill

1. Draw axes.
2. Identify the roots and turning point.
3. Substitute these into the equation y = ax² + bx + c
4. Find c
5. Solve simultaneous equations to get a and b.
6. Use these to find equation of curve.

 

The axes can be placed at your discretion.

Here are three common solutions:

1)

The grid is placed in the centre of the mound, giving a turning point of

(0, 27) and roots at x = -27 and x = 27

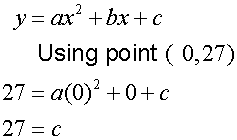
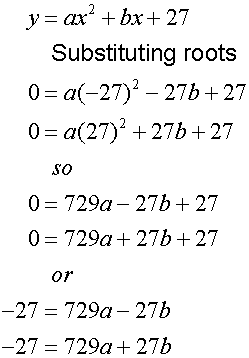
Now solve

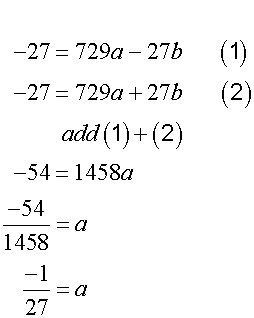
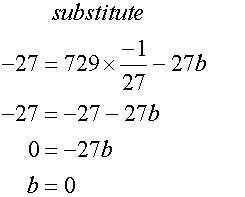
Giving equation

 

 

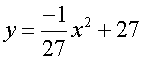
2)

The grid is placed to the left of the mound, giving a turning point of

(27, 27) and roots at x = 0 and x = 54

 

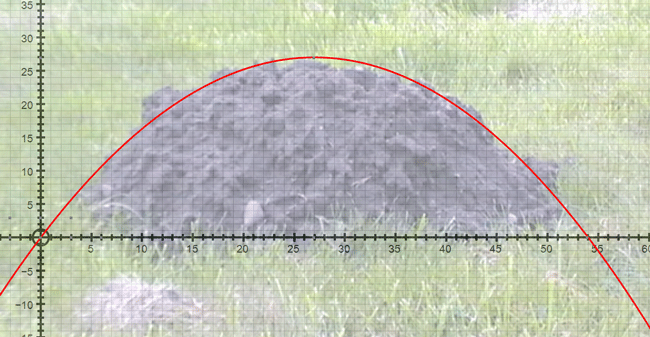
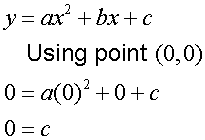
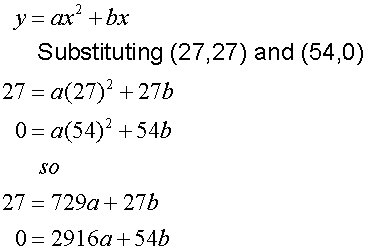
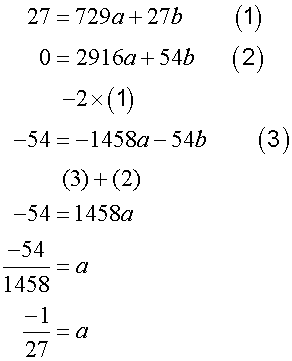
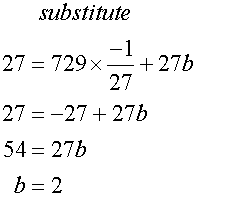
Giving equation

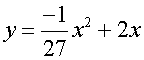
3)

The grid is placed to the right of the mound, giving a turning point of

(-27, 27) and roots at x = -54 and x =0

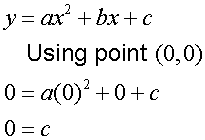
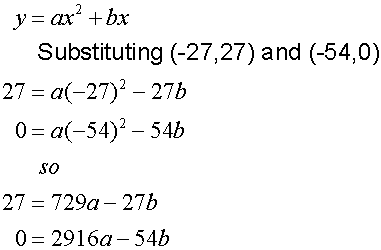
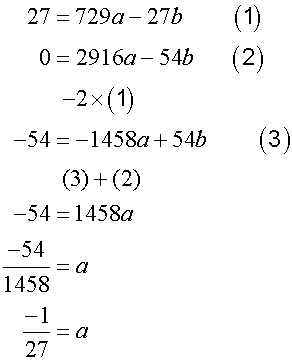
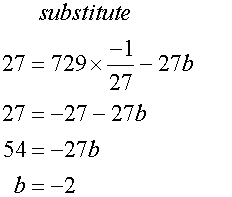
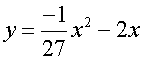
Are these equations all different ?

Yes and no - they are translations of the graph of form

 

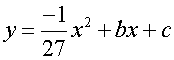
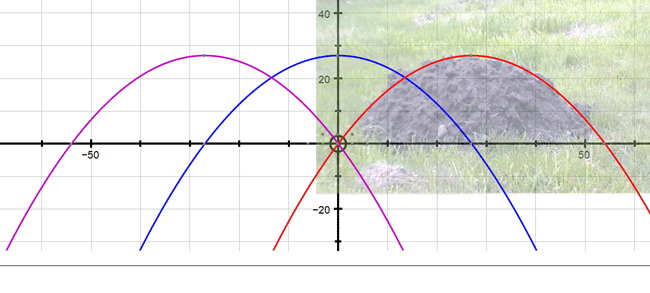
In each case, there is a little extra earth - so the equations approximately describe the outline of the mole hill.

 

Cross sectional area

Using the work from above, the cross section area is found by integrating the equation of the line which describes the outline of the mole hill.

Using the first equation from above,

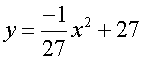
The area under the graph is just the integral between the roots.

 

 

 

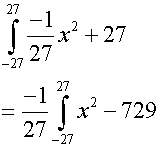
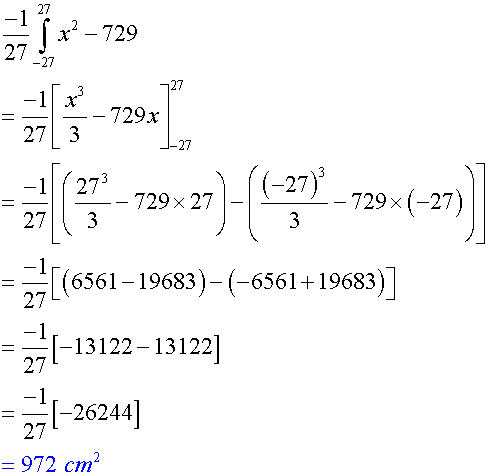
Using the second equation from above,

 

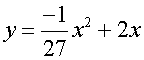
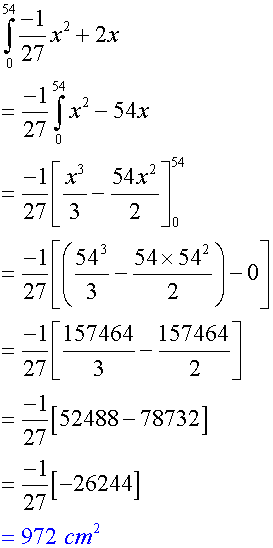
It does not matter which equation is used , the area will remain the same.

 

Circle equations

Using the work from National5 above:

1)

The grid is placed in the centre of the mound, giving the centre of the circle at (0,0) and radius 27cm.

This gives circle equation

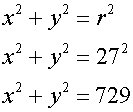
Which can be re-arranged to

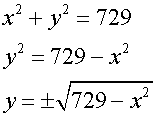
Since it is only the top part of the graph that is required, the positive branch is taken:

 

2)

The grid is placed to the left of the mound, giving the centre of the circle at

(27, 0) and radius 54 cm.

so

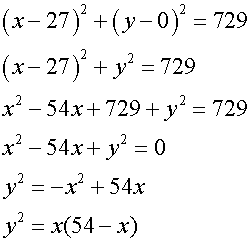
3)

The grid is placed to the right of the mound, giving the centre of the circle at

(-27, 0) and radius 54 cm.

so

 

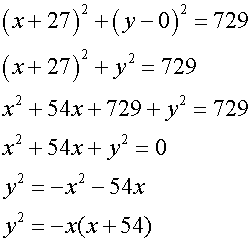
Again, these are all translations of each other.