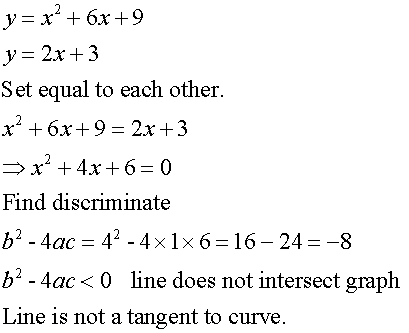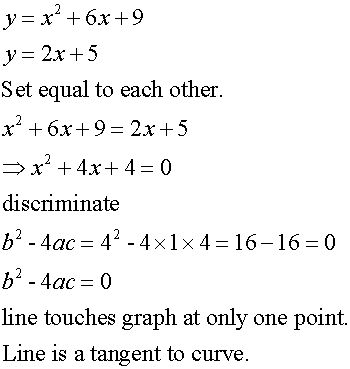Quadratics

Quadratics are polynomials  of degree 2.

They come in many forms, but always have a squared term.

Examples

Quadratic expression :  

     

Quadratic equation: 

      

Quadratic function :  

  

Quadratic graph : 

Quadratic inequation:    

     Quadratic mapping :       

 

Quadratic graphs

   Quadratic graphs have a distinctive U shape
   called a parabola.

  Positive parabolas smile :

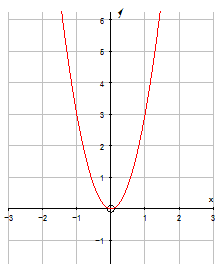y = ax²

 

Negative parabolas frown !

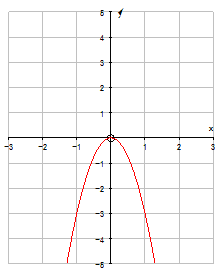y = - ax²

 

Drawing parabolas of the form y = ax²

Pick values for x and put them into a table.

Work out the corresponding for y .

Plot these points and join with a smooth curve.

Example

Complete the table of values for the
equation           y = x²

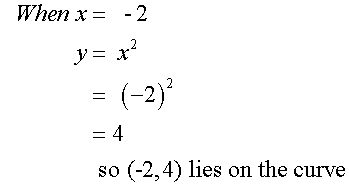
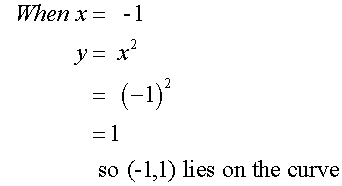
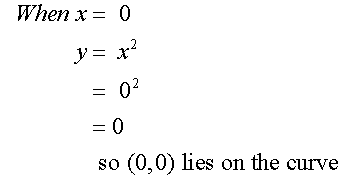
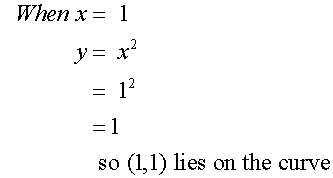
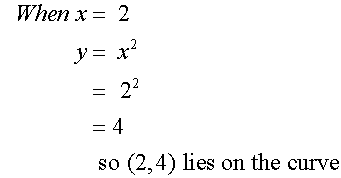
Plotting these points and joining with a smooth curve gives

Notice how the graph is symmetrical !

 

Example

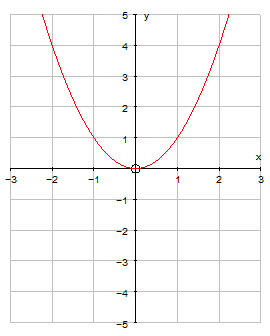
Complete the table of values for the
equation           y = -5x²

 

 

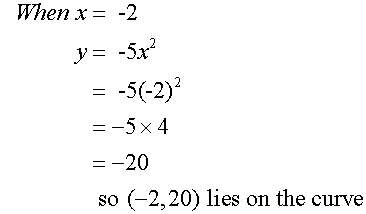
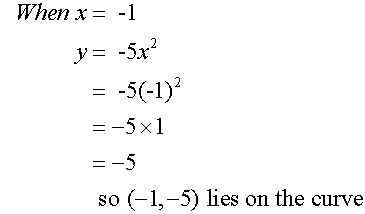
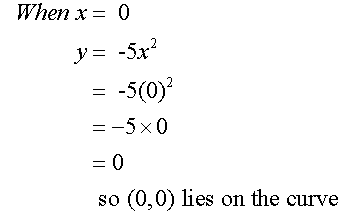
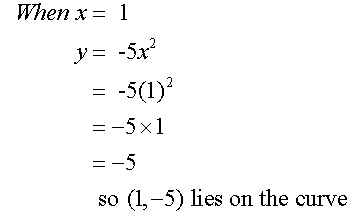
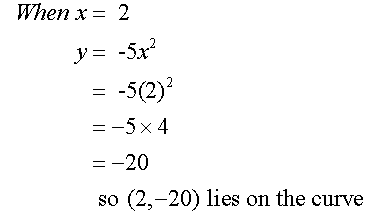
Plotting these points and joining with a smooth curve gives

 

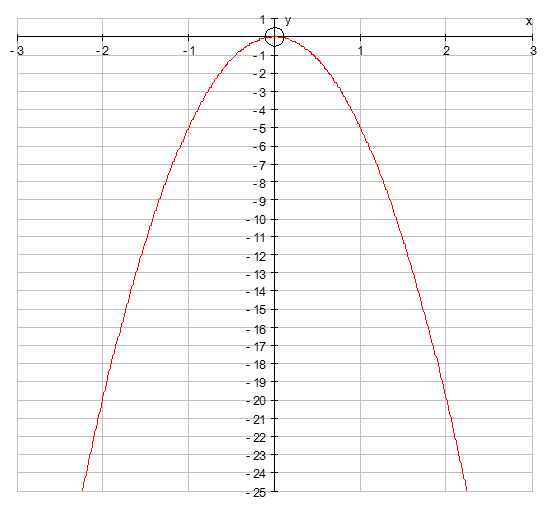
Again, notice how the graph is symmetrical !

 

Working backwards

Example

Find the equation of the following parabola
      of the form y = ax²

 

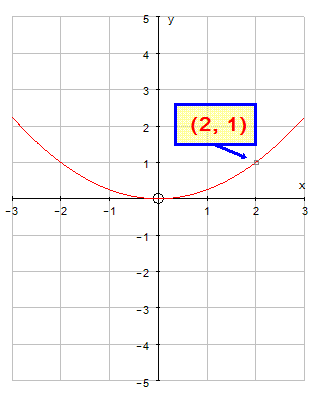
The graph is of the form y = ax²
The given co-ordinate is ( 2, 1 )
So x = 2 and y = 1 are on the curve

Substitute and solve

 

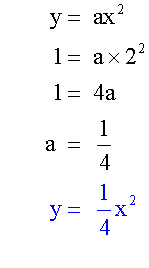
Parabolas of the form y = a(x-b)²

Example

Complete the table of values for the
equation y= (x-2)²

 

 

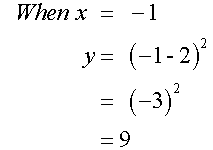
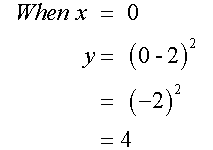
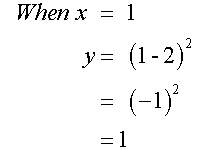
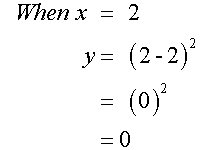
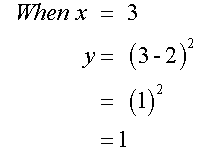
Plotting these points and joining with a smooth curve gives

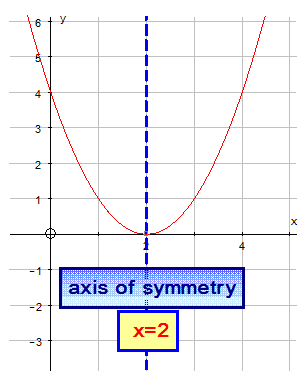
This time,the graph is symmetrical when x=2

The turning point is (2,0)

 

The axis of symmetry is the b
in the equation   y = a(x-b)²

 

Example

Find the equation of the following parabola
      of the form y = a(x-b)²

 

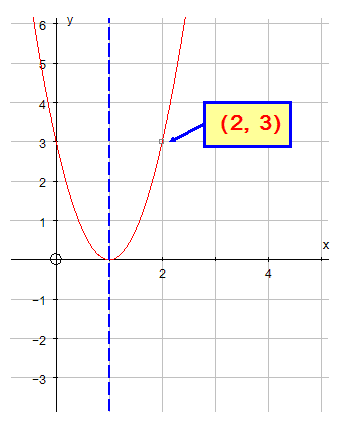
The graph is of the form y = a(x-b)²
The given co-ordinate is ( 2, 3 )
So x = 2 and y = 3 are on the curve
Substitute and solve

 

 

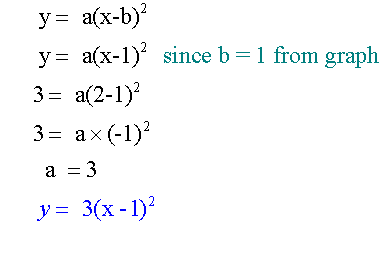
Parabolas of the form y = a(x-b)² + c

Example

Complete the table of values for the equation
  y= -2(x+3) ²+ 2

 

 

 

 

 

 

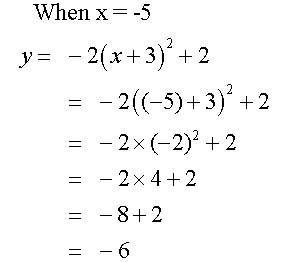
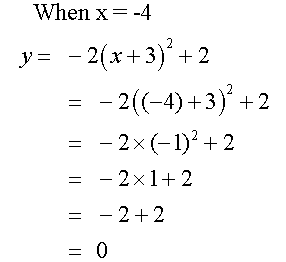
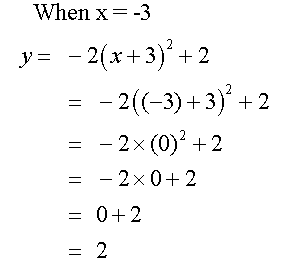
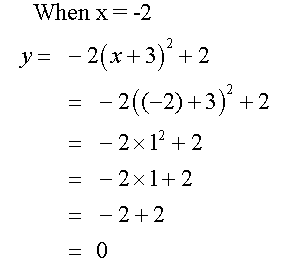
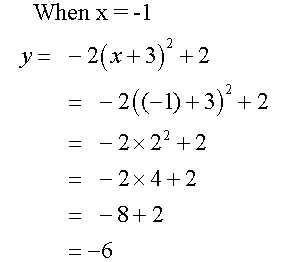
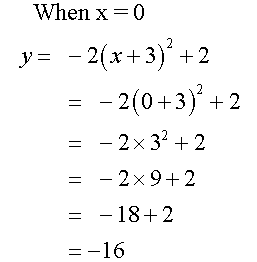
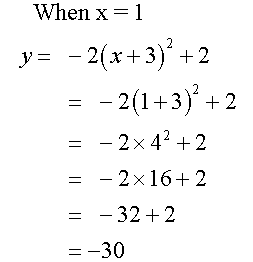
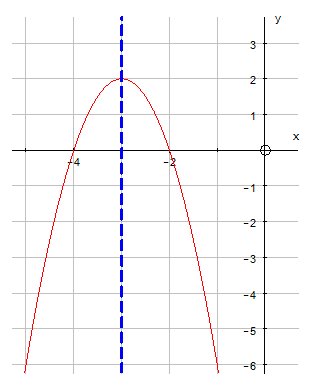
Notice that the axis of symmetry is x = - 3

 

Working Backwards

Example

Find the equation of the following parabola
      of the form y = a(x-b) ² + c

 

 

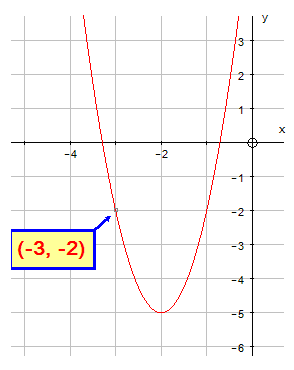
The graph is of the form y = a(x-b)² + c

The given co-ordinate is ( -3, -2 )
So x = -3 and y = -2 are on the curve

From the graph, b = -2 since it is the axis of symmetry.

Substitute x= -3, y=-2 and b = -2

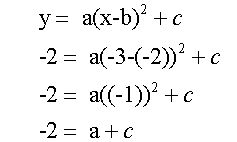
The point (-2,-5) is also on the curve.

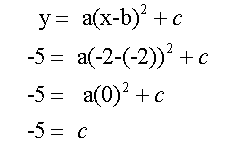
So c = -5

Substitute  into -2 = a +c

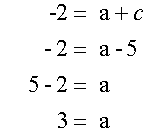
Substituting a, b and c into the original equation
      y = a(x-b)² + c

Axis of symmetry

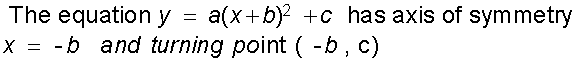
This is a quadratic in completed square form.

Example

Find the axis of symmetry of the line y = x²+3x+2

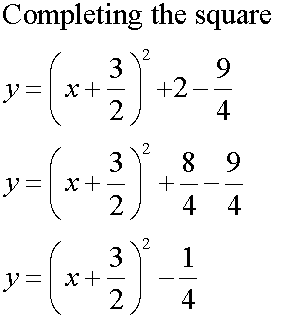
The axis of symmetry is x = -3/2

Completing the Square

 

Parabolas of the form y = ax² + bx + c

Example

Complete the table of values
for the equation  y= 2x²+3x - 2

 

 

 

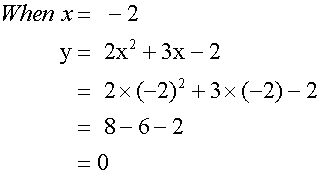
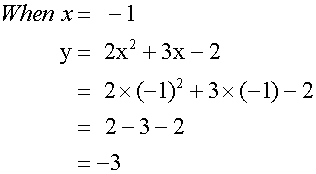
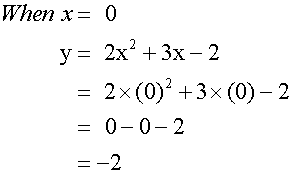
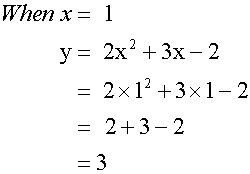
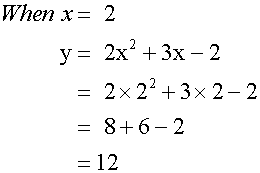
Turning Points

Positive parabolas have a minimum turning point.

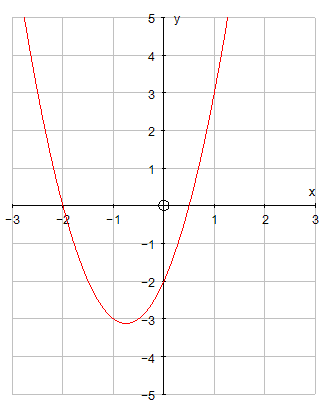
Example

Find the turning point of the quadratic

y = x² + 3x + 2

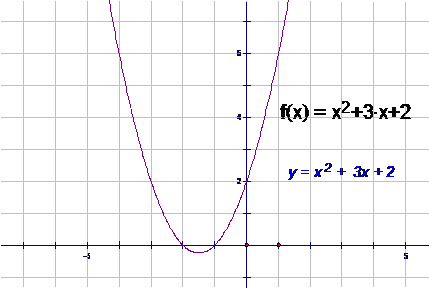
The turning point occurs on the axis of symmetry.

 

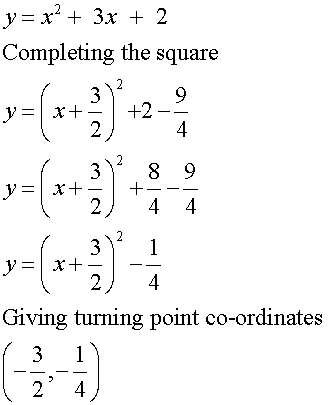
Negative parabolas have a maximum turning point.

Roots

A root of an equation is a value that will satisfy
the equation  when its expression is set to zero.

Eg  0 = x² +2x -3

The maximum number of roots possible
is the same as the degree of the polynomial,
so a quadratic can have a maximum  of two  roots.
Not all quadratics have roots.

 

To find the roots of a quadratic,
Sketch the graph and see where it cuts the x axis.

Or

Set y = 0  and factorise (If possible)

Example

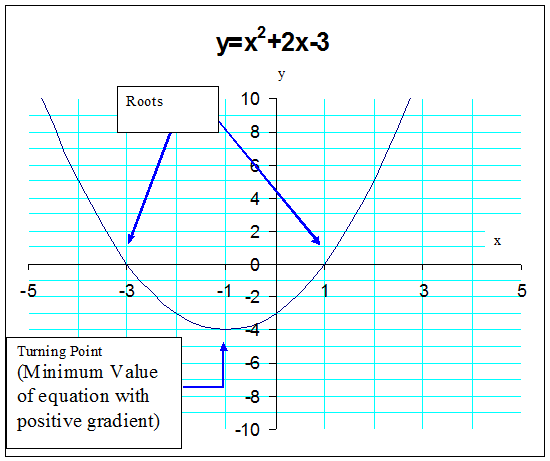
From the graph, the  equation y = x² + 2x –3 has roots
   x = -3 and x = 1

 

This is the same as setting y to zero and factorising:-

        

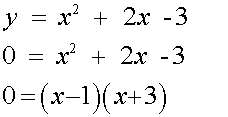
Either bracket can equal 0 , so both must be considered:

 

 

Excel spreadsheet

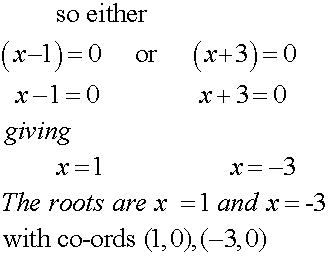
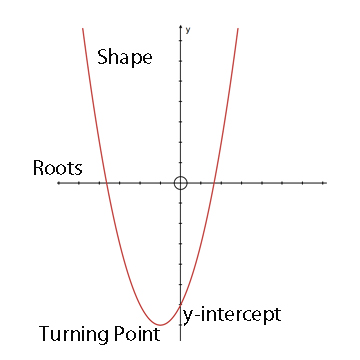
Sketching parabolas

 

Remember : Shape, roots, turning point, y-intercept.

 

Example

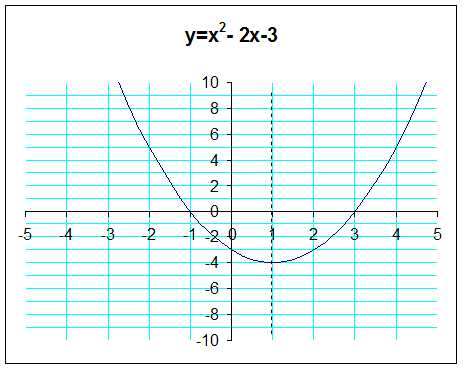
   Sketch  y = x² - 2x - 3

This will be a U shape, since a = 1

It will cut the y-axis at (0,-3)

  

 

 

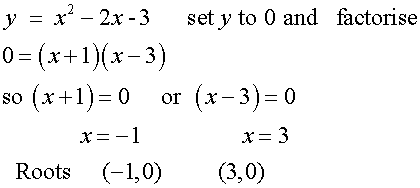
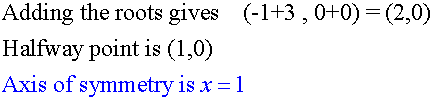
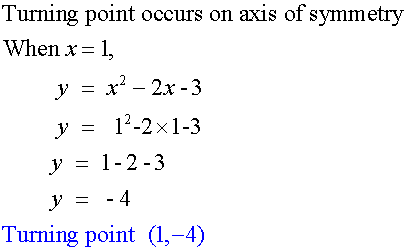
Example

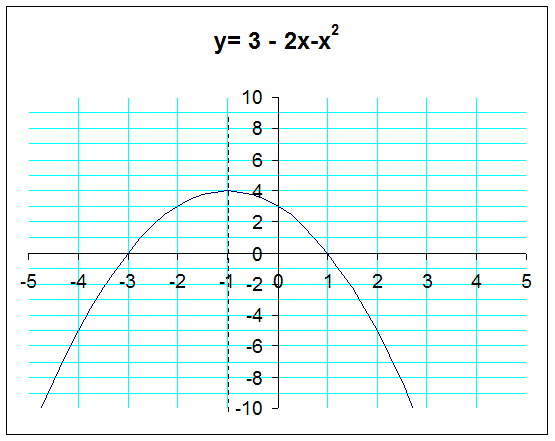
  Sketch  y = 3-2x-x²

                       

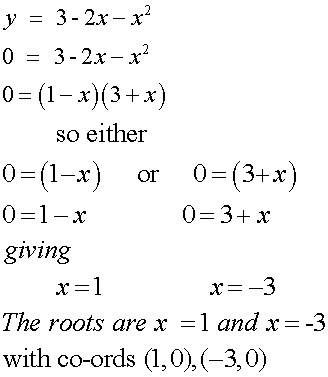
   This will be a ∩ shape, since a = -1

It will cut the y-axis at (0,3)

 

 

 

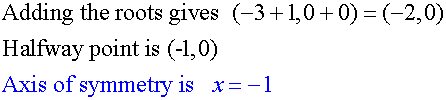
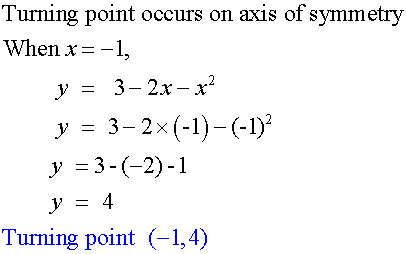
Quadratic equations

Standard form Quadratic equations are of the form

To find the solution of a quadratic equation :

Rewrite the expression in standard quadratic form

Factorise if you can:

{Remember to look for common factors and the difference of two squares}

Use the quadratic formulae

   

Examples

Solve 3x - 6x² = 0

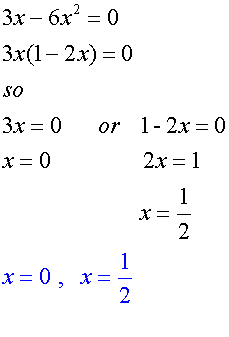
Solve 49 - 9x² = 0

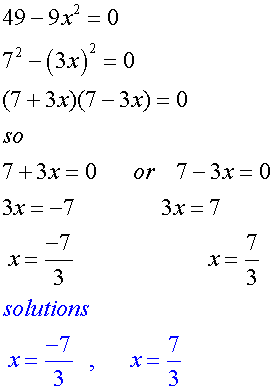
Solve 15x² - x - 6= 0

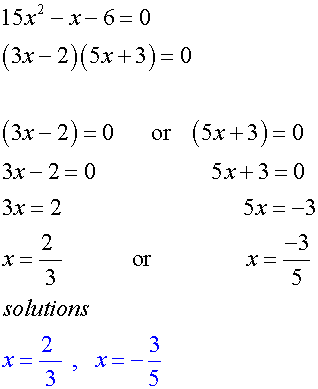
Solve 15x² - x +1= 7

 

 

Factorising Quadratics             

 

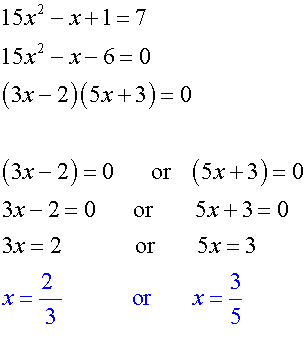
Quadratic Formula

 If the quadratic does not factorise,

try the quadratic formula :

 

Examples

Solve 2 + 4x -5x² = 0

Give your answer as a surd.

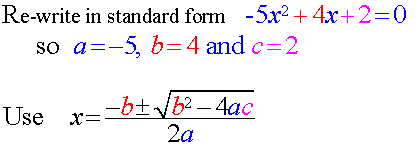
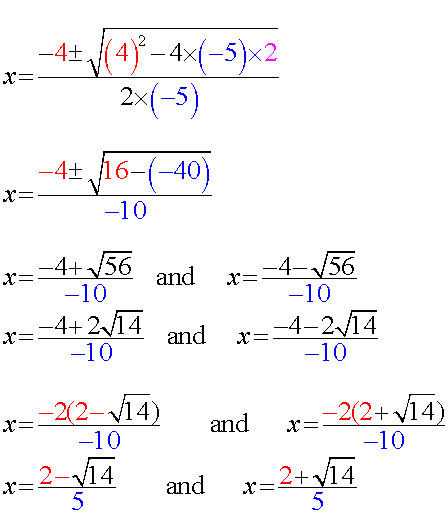
Example

Find the roots of 2 + 4x -5x²

Give your answer correct to two decimal places.

 

 

 

     Not all quadratics factorise  

 

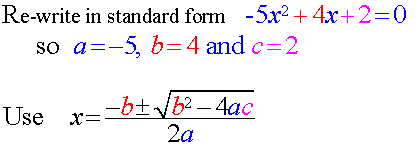
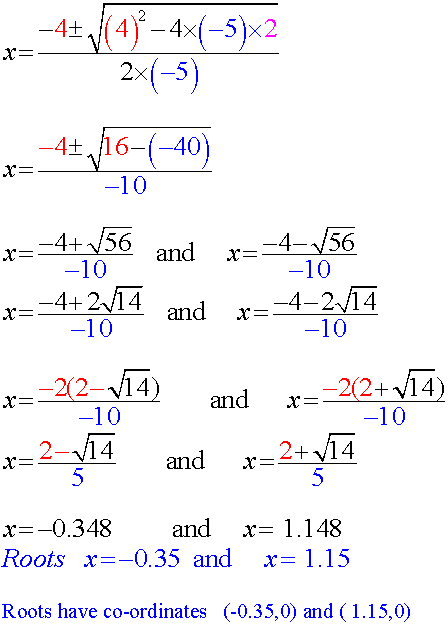
Discriminant

     

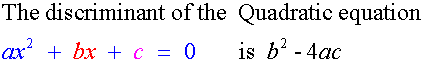
Examples

    
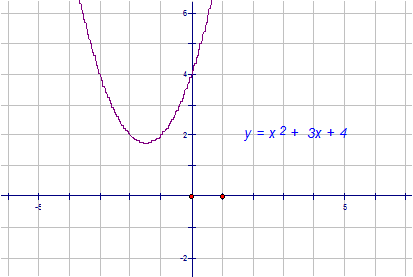
Discriminant
b²– 4ac
= 3²- 4x1x4
= 9 – 16
= - 7

b² – 4ac < 0
No real roots

 

 

 

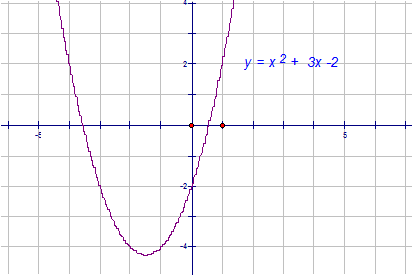
b² – 4ac
= 3²- 4x1x(-2)
= 9 +8
= 17

b² – 4ac > 0
Two distinct, real roots

 

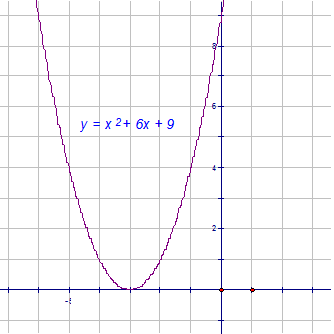
b² – 4ac
= 6²- 4x1x9
= 36 – 36
= 0

b² – 4ac = 0
Roots are equal and real

 

Working Backwards

Example

The roots of   ( x – 1)( x + k) = -4  are equal.
Find the values of k.

First multiply out the brackets

      

 

 

 

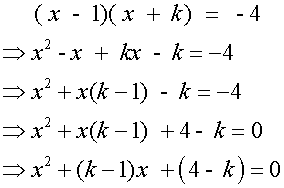
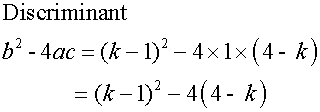
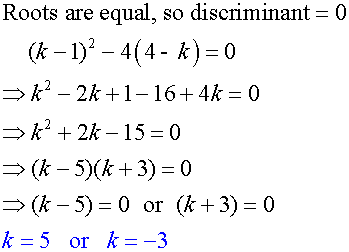
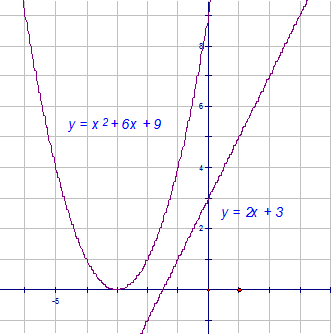
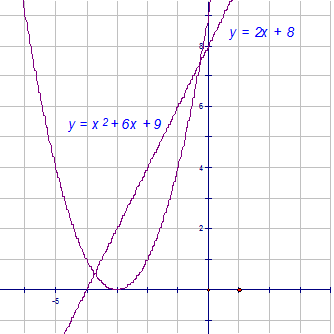
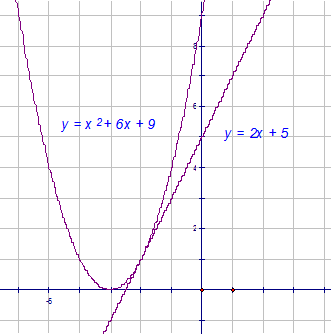
Tangency

 A tangent to a curve  touches the curve at one point only.
To test for tangency, set the two functions equal to each other
and find the resulting discriminant.

If     b² – 4ac > 0   , the line cuts at two distinct points.
It is not a tangent.

If    b² – 4ac < 0   , the line does not touch the curve.
It is not a tangent.

If     b² – 4ac = 0   , the line touches the curve at only one point.
It is  a tangent.

 

Examples