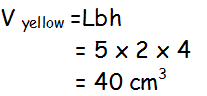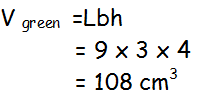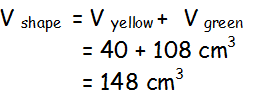Perimeter, Area and Volume

 

Perimeter

Perimeter = distance around the edge.

You could walk around the perimeter.

All dimensions must have the same units !

Don't mix cm with m.

Perimeter has plain units.

 

Example

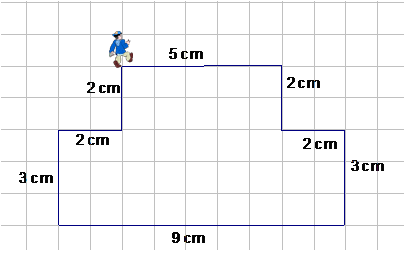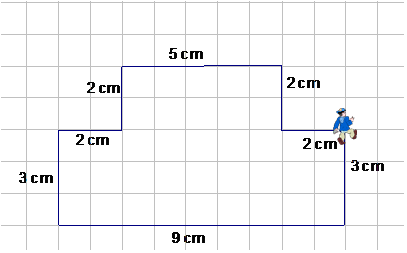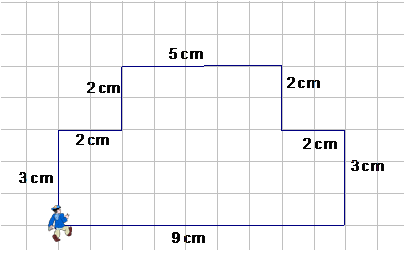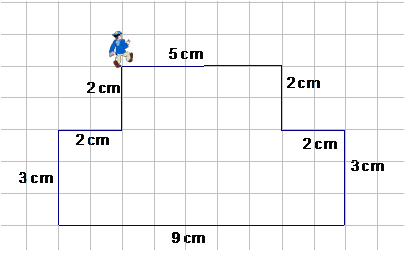
P = 5 + 2 + 2 + 3 + 9 + 3 + 2 + 2 cm
P = 28 cm

 

Area

Area = floor space covered

 

 

You could paint an area.

All dimensions must have the same units !

Don't mix cm with m

Area  has units².

 

1m² = 10,000 cm²

 

Area of a square

      

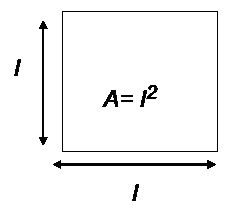
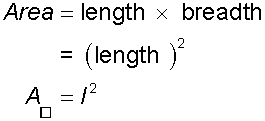
Example

Calculate the area of the square

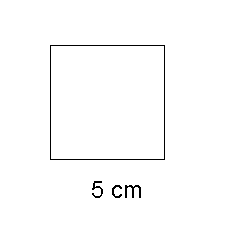
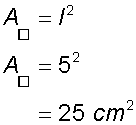
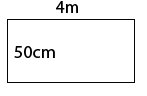
Area of a rectangle

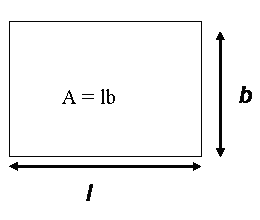
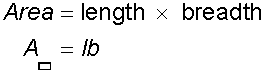
Examples

Calculate the area of the rectangles

 

   

 

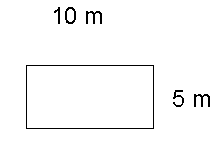
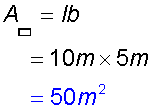
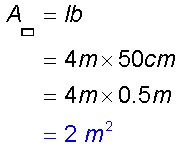
Area of a triangle

Area of a triangle = ½ x base x perpendicular height

 

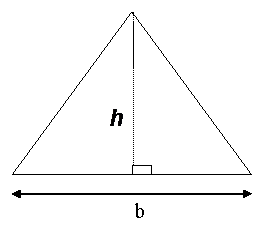
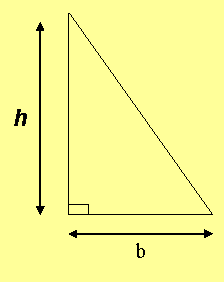
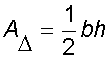
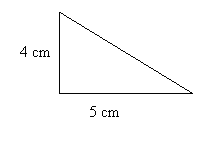
Examples

Find the area of the triangle below:

 

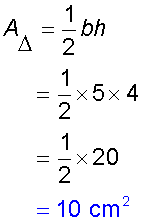
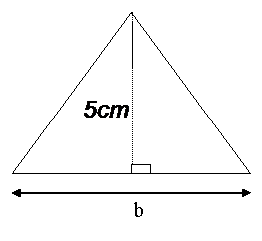
What is the length of the base of the triangle, if it has an area of 45 cm² ?

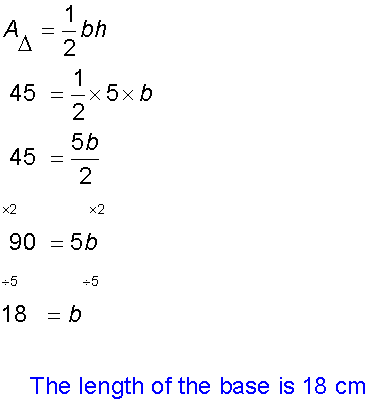
Area of a triangle - using Trigonometry

 

Area of a circle

Examples at Area of a circle

Area of kite

   

 

  

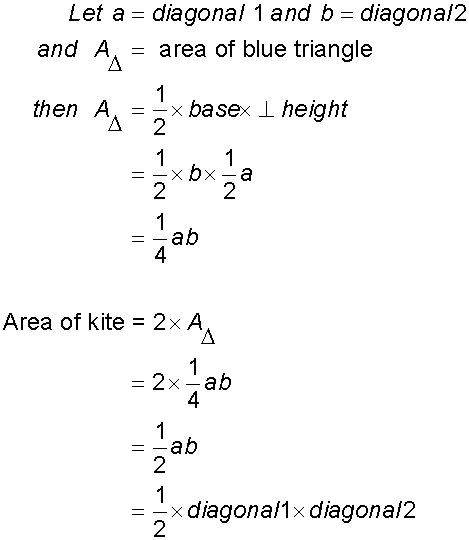
Example

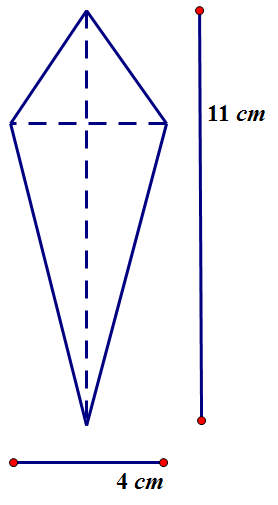
Calculate the area of the following kite:

 

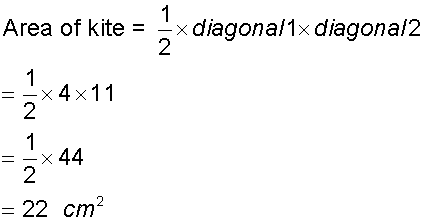
Area of Trapezium

 

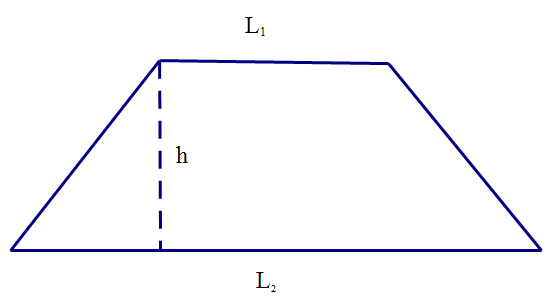
Area of a trapezium = ½ x average of base x perpendicular height

 

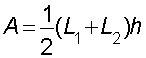
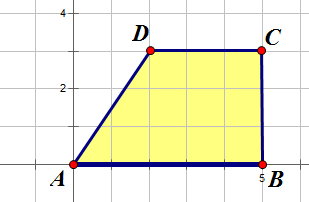
Example

What is the area of this trapezium ?
(Each square represents 1 cm² )

  

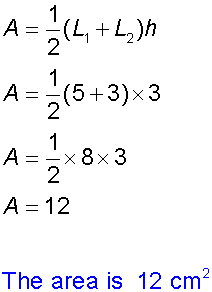
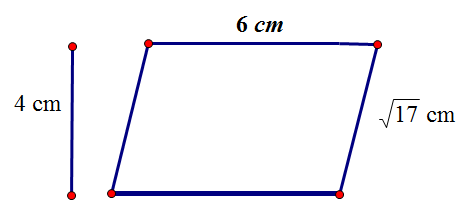
Area of a parallelogram

 

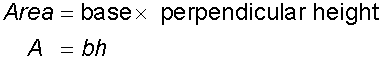
Example

Calculate the area of the parallelogram :

 

 

 

Area of a rhombus

 

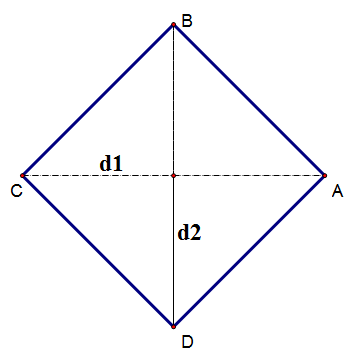
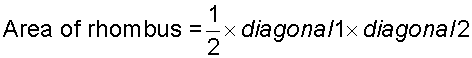
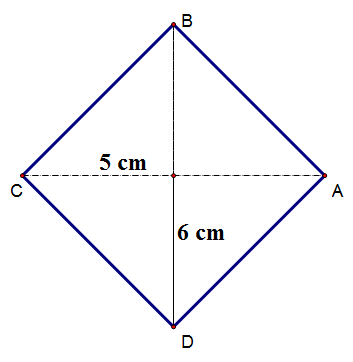
Example

Calculate the area of the rhombus:

( The sizes are for the complete diagonals)

 

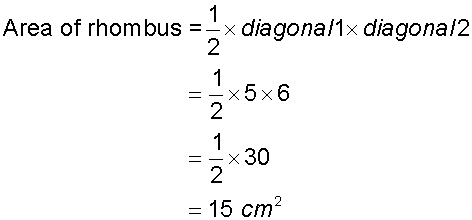
Volume

Volume = capacity held

You could fill a volume

All dimensions must have the same units !

Don't mix cm with m.

 

Volume  has  units³

Notice that for a cuboid

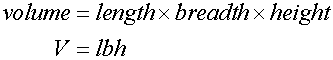
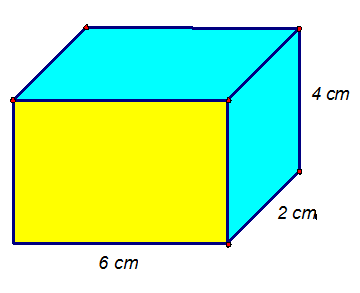
Example

Calculate the volume of the cuboid below:

 

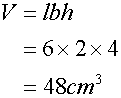
Example

Converting 1m³ to litres

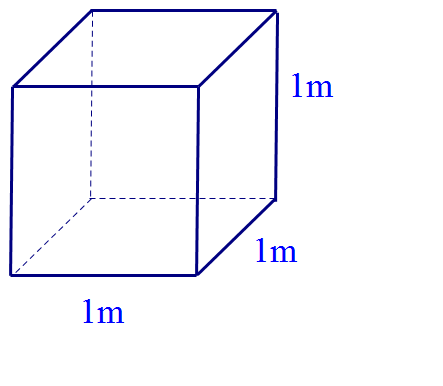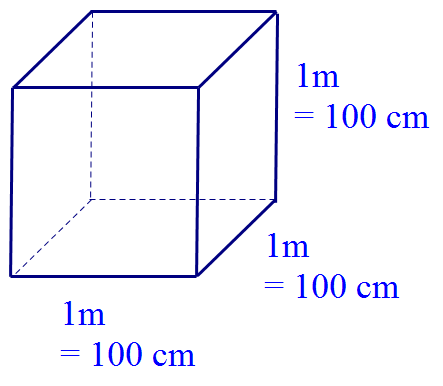
First, convert the units

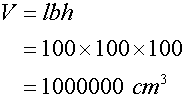
But 1 cm³ = 1 ml and 1000 ml = 1litre
Divide cm³ by 1000 for litres.

So  1 000 000 cm³ = 1000 litres
           1 m³ = 1000 litres

 

Volume of a Sphere

A sphere has volume

  

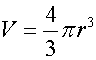
Where r is the radius of the sphere.

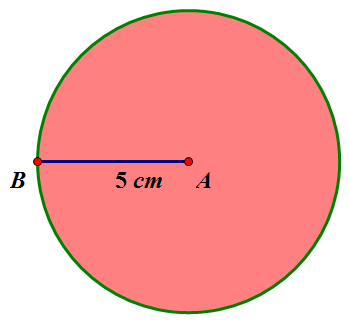
Examples

Calculate the volume of the following sphere.
Give your answer correct to 1 dp and also to 2 sig figs.

 

 

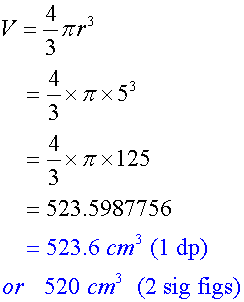
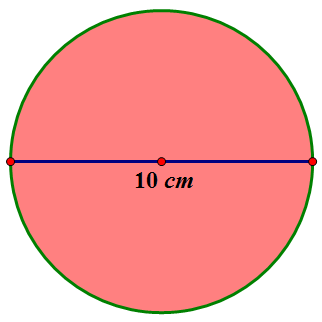
Calculate the volume of the following sphere.
Give your answer correct to 1 sig fig.

  

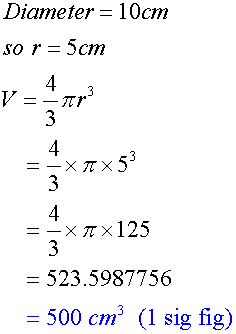
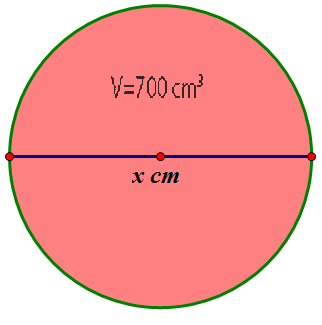
Calculate the diameter of a sphere which has a volume of 700cm³.
Give your answer correct to 1 dp.

 

  

 

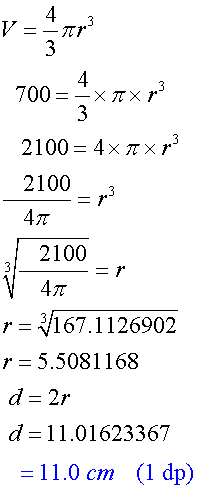
Volume of a Cone

 

A cone has volume

  

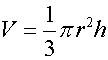
Where r is the radius of the circular part of the cone  and h is the perpendicular height of the cone.

 

 

 

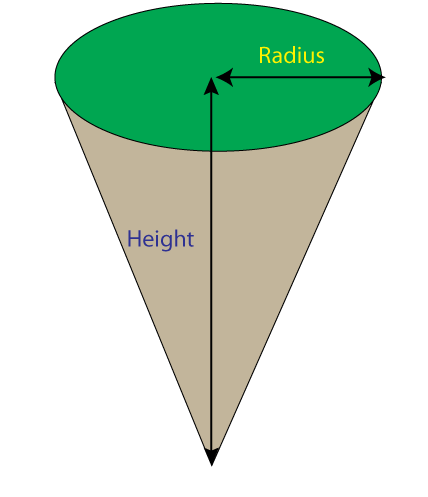
Example

Calculate the volume of an ice cream cone which has a diameter of 4cm and a height of 6cm. Give your answer correct to 1 dp.

 

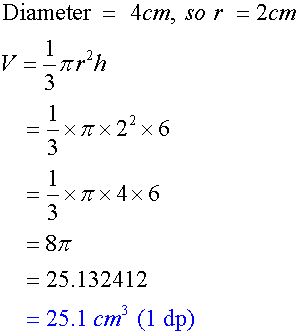
How many of these cones can be filled from 1litre of ice cream ?
1000 cm³ = 1 l

1000 ÷ 25.1 = 39.84
So 39 cones can be filled from one litre of ice cream.

 

Example

Calculate the height an ice cream cone which has a diameter of 4cm and a volume of 35ml. Give your answer correct to 1 dp.

 

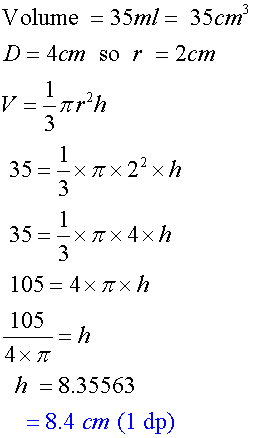
The cone is 8.4 cm tall.

 

Example

Calculate the diameter of an ice cream cone which has a height of 8cm and a volume of 90ml. Give your answer correct to 1 dp.

 

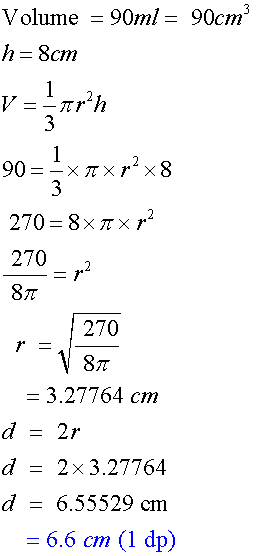
Volume of a prism

For a prism,  V=Ah

So Volume = Area x height   (or Area x Length if laying down)

Example

What is the volume of  a prism which has an area of 37 cm²    and a height of 4 cm ?

Volume of a cylinder

 A cylinder is a circular prism,

 

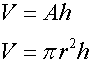
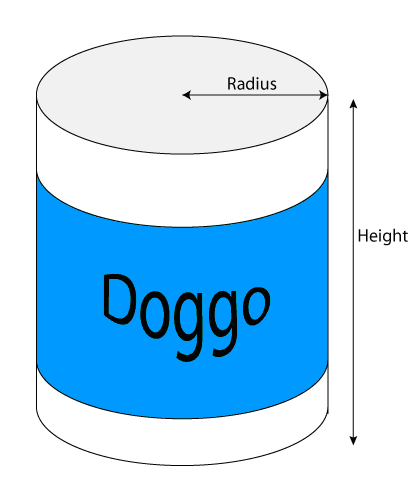
Example

Calculate the volume of a tin can which has a height of 0.8m and a diameter of 10 cm. Give your answer correct to 1 sigfig.

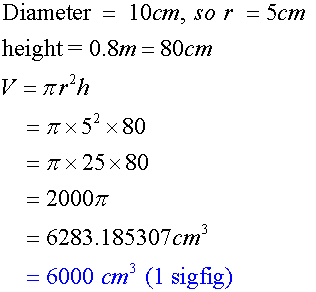  <br>

This is 6 litres, since 1000cm³= 1 litre

Example

Calculate the diameter of a tin can which has a height of 8cm and a volume of 90ml. Give your answer correct to 1 dp.

 

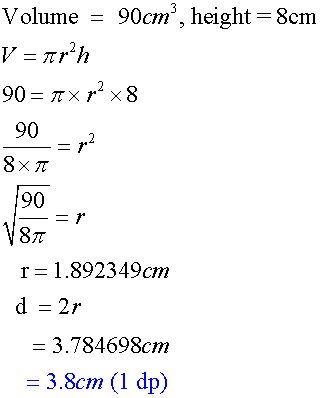
Volume of a pyramid

The volume of any pyramid is given as

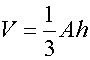
where A is the area of the base of the pyramid and h is its height.

Examples

What is the volume of this squared based pyramid ?

 

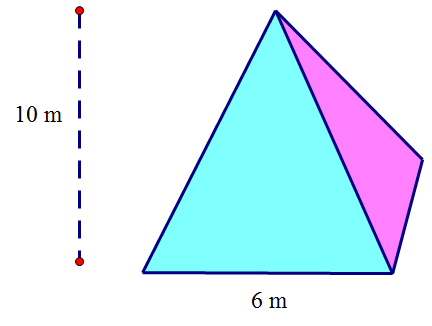
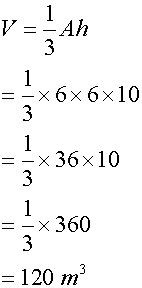
What is the volume of this rectangular based pyramid ?

 

 

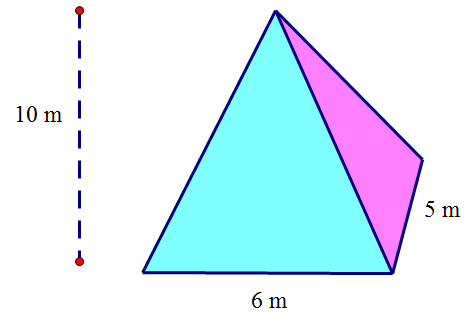
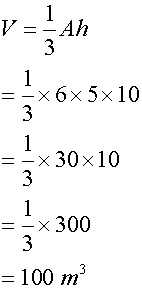
What is the volume of this triangular based pyramid ?

 

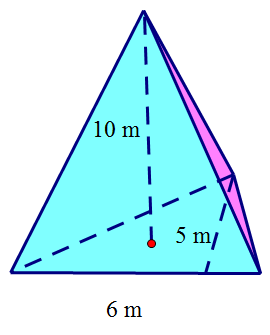
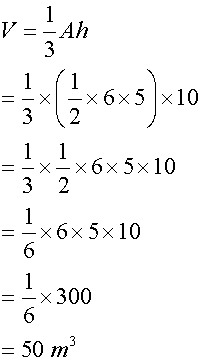
Surface area

The surface area is the total external area
of the shape.

 

Example

Find the surface area of the cuboid :

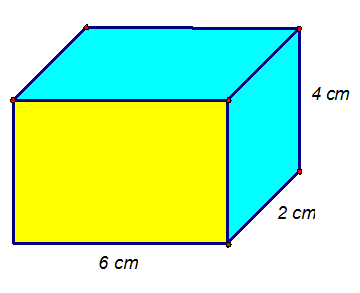
This shape has 6 faces

2 faces have area    6cm x 4cm
2 faces have area    6cm x 2cm
2 faces have area    2cm x 4cm

    2 x 6cm x 4cm =  48 cm²
    2 x 6cm x 2cm =  24 cm²
    2 x 2cm x 4cm =  16  cm²
     Surface Area =   88  cm²

 

Surface Area ≠Volume

 

Composite area

Cut into convenient shapes
Find missing dimensions
Calculate individual areas
Calculate  total

 

Example

 

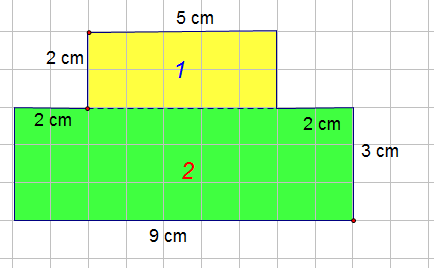
A shape = A 1 + A 2
A 1 = 5x2 = 10 cm²
A 2 = 3x9 = 27 cm²
A shape = 37 cm²

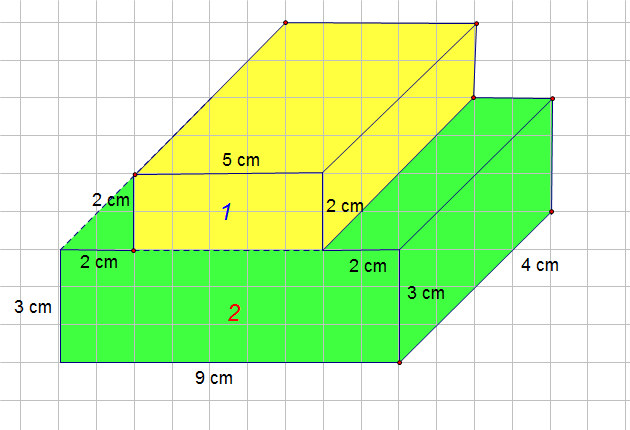
Composite Volume

Cut into convenient shapes
Find missing dimensions
Calculate individual areas
Calculate  total

Example