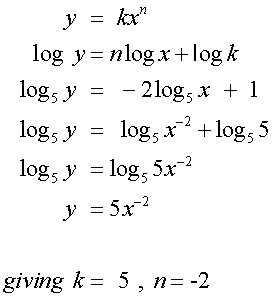Exponentials
An exponential is a power , otherwise known as an index
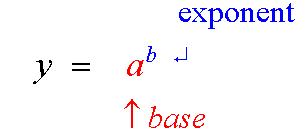
A base number is raised to a power, the exponent.
Example
73 has base 7, exponent 3
73 means 7x7x7 , which has value 343
The inverse of an exponential function is called the logarithmic function
If y = ax
then x = loga y
To solve an exponential, take logs of both sides to the same base.
Scientific calculators usually have buttons for :-
Common logarithms natural logarithms
log for logarithms to base 10 ln for logarithms to base e =2.71828…
Example
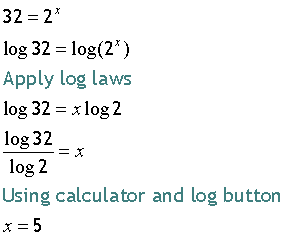
also

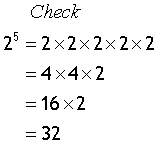
The natural base: e
The natural base, e , uses Euler's number e = 2.71828182…
y = ex has the special property that
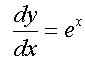 , which is useful for differentiation at Advanced Higher
, which is useful for differentiation at Advanced Higher
The inverse of y = ex is x = logey, written x = ln y
Graphing Exponential and Logarithmic functions Excel -Exponential / log functions - graphs
Growth functions
A growth function is one where the output increases rapidly.
Example
£100 is deposited in a bank at a fixed rate of 12% per annum.
If A(n) = the amount of money in the account after n years,
a) show that A(n) = 100 x 1.12n
b) calculate the amount in the account after 10 years.
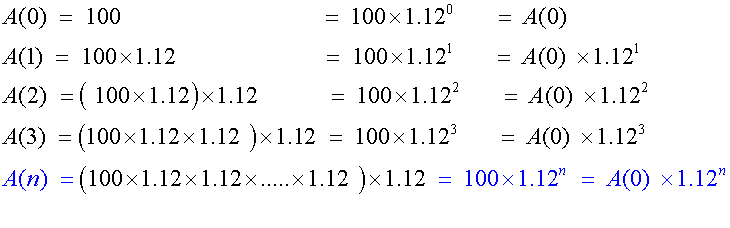

{This is the background behind CRy }
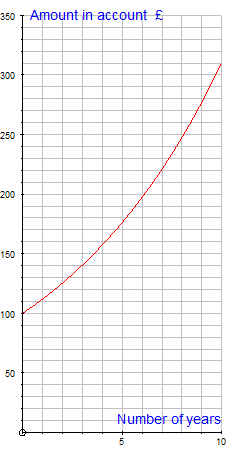
The account growth looks like this:
Example
A factory has a target of 1.5% increase in output per year.
In 2003, the production was 18000 units.
In 2005, the production was 18515 units.
Was the production target met?

Decay functions
A decay function is one where the output decreases rapidly.
Example

8000 gallons of oil are lost in an oil spill.
The clean up crew manage to clean 67 % of the oil each week.
a) How much oil is left after 1 week ?
b) How many weeks of cleaning are needed for there to be 10 gallons left ?
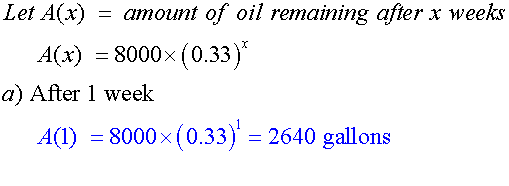
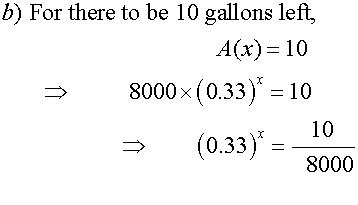

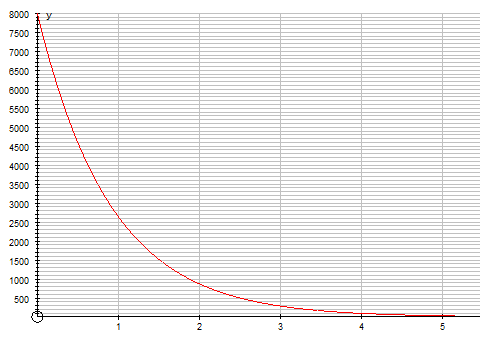
The oil spill decay looks like this:
Half life
The rate of decay of a radioactive source can be represented by the equation
![]()
where N is the number of radioactive atoms present at time t , λ is the transformation decay constant and No is the original starting value.
The half-life of carbon-14 is 5,730 ± 40 years and is used for radio carbon dating
Example
Given a half life of 5730 years, calculate the decay constant λ.
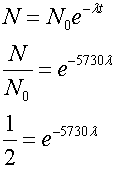
so
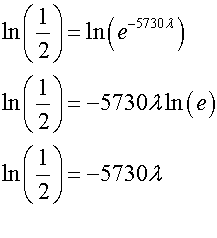
giving
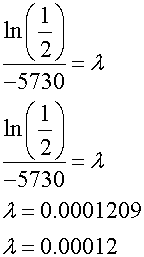
Log - Linear Graphs
Log scale Y axis only
If you have a graph with a logarithmic y axis, but ordinary x axis
then a straight line log y = (log b)x + log a
confirms a relationship of the form y = abx
for suitable constants a and b.
If y = abx then log y = log a + xlogb
This is because of the log laws
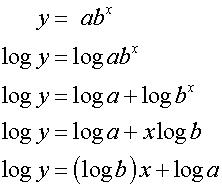
Compare this to Y = mx + c
where Y = log y, m = log b and c = log a
Example
Find the equation of the graph below in the form y = abx
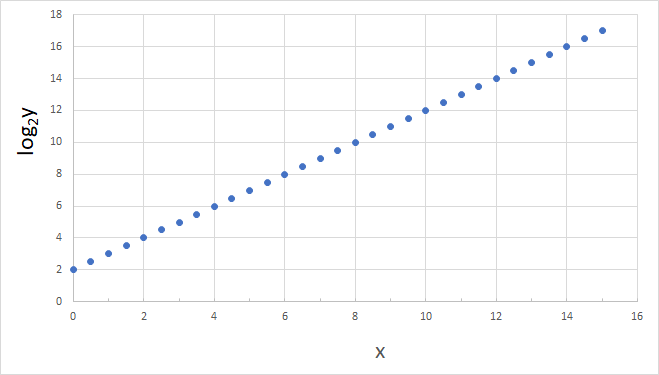
The points (0,2) , (2,4) , (6,8) and (10, 12) lie on this graph,
giving c = 2 and m = 1
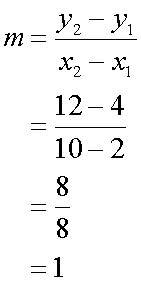
Now,
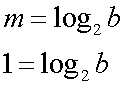
and
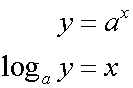
so
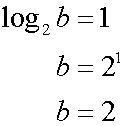
Likewise,
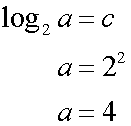
Putting all together, a =4, b = 2 so writing in the form y=abx the graph is y = 4(2x)
This is not the same as y = 8x , just as 2 x 42 is not equal to 82
Notice :
When x = 0
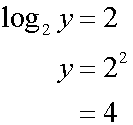
When x = 2
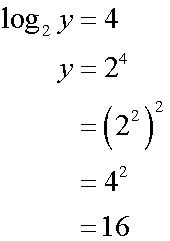
When x = 6
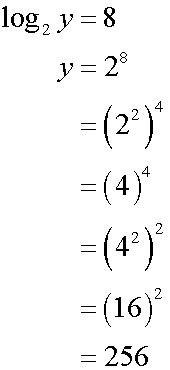
When x = 10
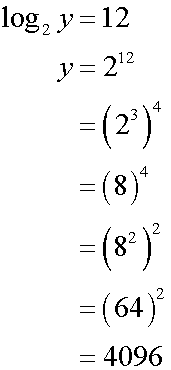
Giving points (0,4) , ( 2, 16) ,( 6,256 ) and ( 10, 4096 )
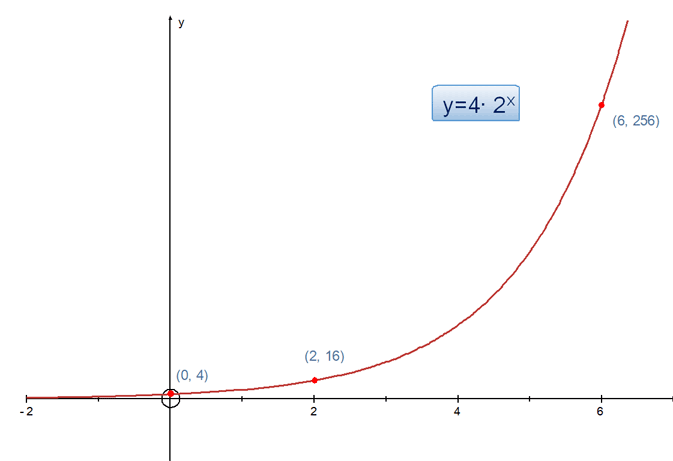
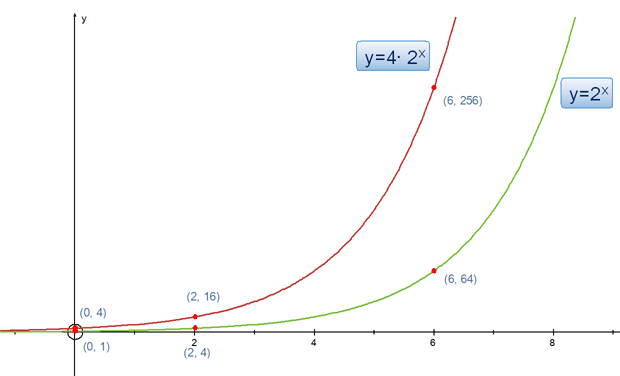
Comparing with y = 2x , it can be clearly seen that the graph has been scaled by a factor of 4 in the y direction.
Example
Show that the formula connecting the following
data is of the form y = abx .
Find the value of a and b and state
the formula that connects x and y.

Solution
To show that y and x are related by the formula y=abx
- Take logs to base 10 of y.
- Plot against x.
A straight line confirms that a relationship exists.
Taking logs to base 10 of y gives
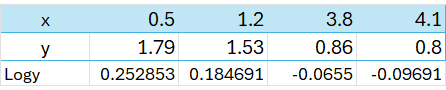
Plotting logy against x gives
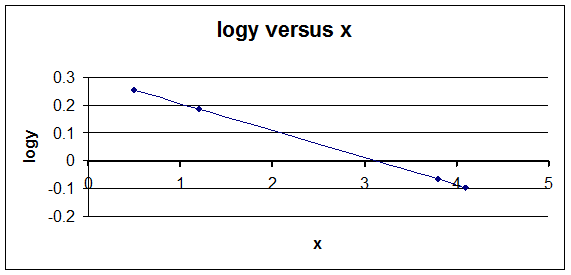
- Now take two points on the line of best fit to work out the gradient and y-intercept.
- Use Y = mX + c, with Y = log y, m = logb , c=loga
- Solve as simultaneous equations
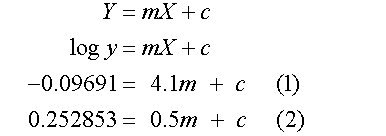
Now find m
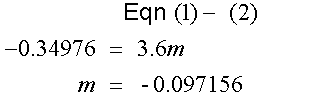
Use this to find b
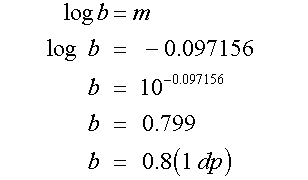
Substitute to find c
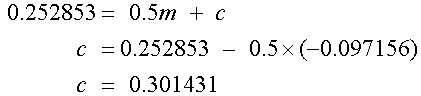
Use to find a
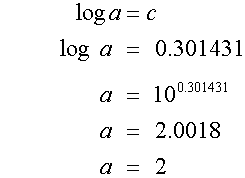
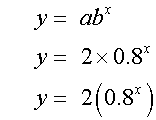
Log - Log Graphs
Log scale both axis
If you have a graph with a logarithmic axes on both axes,
then a straight line
log y = b log x + log a
confirms a relationship of the form y = axb
for suitable constants a and b.
If y = axb then log y = blog x + log a
(When both, blog ! )
This is because
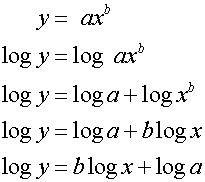
Compare this to Y = mX + c
where Y = log y, X = logx and c = log a
Example
Show that the log - log graph below has equation

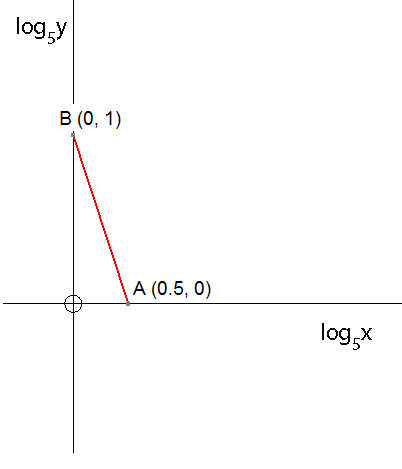
Solution
Gradient of BA is

Line cuts x-axis at ( 0, 1) , so c = 1
Graph is of the form Y = nX + c
Where Y = log5y , X = log5x and c = log5x