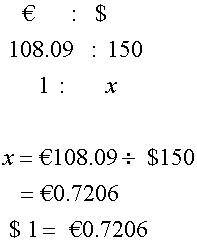Utility Bills

Telephone, Gas  and  Electricity bills usually have a standing charge, plus
a cost for each unit used. VAT is payable on top of this.

 

Number of units used = Present reading – Previous reading
Total charge for units = Number of units used x Cost per  Unit
VAT is payable on the whole bill

 

Loans

   Secured Loans – If you default on payments, your house is at risk.
  Unsecured Loans – The goods bought are yours. Your house is safe.
  Hire Purchase – The goods bought are not yours until the last payment has been made.
  Mortgages – Secured loans for Houses, Ships, etc.

Example

Joe Bloggs wishes to borrow £10,000.
Which of the following  options is the cheapest way to borrow ?

 

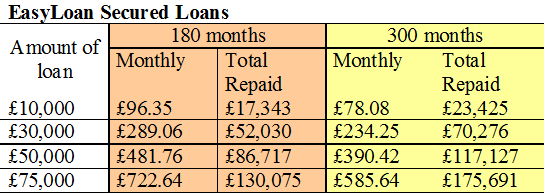
The cheapest way with EasyLoan  costs  £17,343 for 15 years .
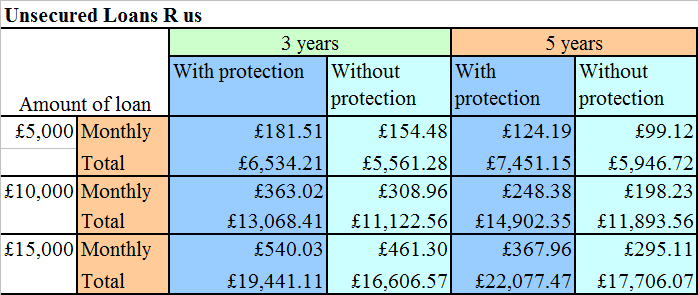
The cheapest way with Loans R us    costs £11,122.56 for 3 years (unprotected.)

Fred’s Finance costs

Cheapest method is with Loans R us  for 3 years (unprotected.)  

Hire Purchase (HP)

With Hire Purchase, a deposit is paid and is then followed by a set amount of monthly repayments. Sometimes, a final payment is also made.

The goods are not yours until the final payment is made.

Example

A television costs £600 cash.
It is available on HP for a 10% deposit
followed by 36 monthly instalments of £ 15.75

How much cheaper is to pay cash ?

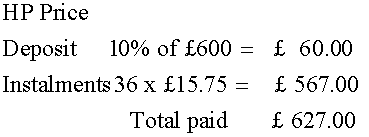
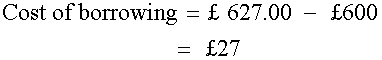
It is £27 cheaper to pay by cash.

 

Car Finance

 

There are a few options available when buying a car :

Cash: You buy the car outright.

Car loans: You buy the car outright and spread the cost over a longer period of time.

Hire Purchase (HP): Spread the cost of the car over several months or years. You'll own the car outright once you've made all payments.

Personal Contract Purchase (PCP): Take out a loan to cover the car's depreciation. You have the option to buy the car at the end of the contract.

Leasing: Personal Contract Hire (PCH) :A long-term car rental contract where the car never actually belongs to you.

 

Hire Purchase (HP)

Hire Purchase allows you to buy a car without having to pay the full amount upfront. A monthly fee is paid to hire the car, which covers the cost of the car as well as interest charges. The car remains the property of the HP company until the final payment has been made.

Key features of Hire Purchase

• Contracts can be up to 5 years long.
• The cost can be spread to suit your circumstances.
• The car is yours to own at the end of the agreement.
• There are no mileage restrictions.
• You choose how much deposit you put down at the start of the agreement.

Risks of Hire Purchase

• You do not own the car until the final payment is made.
• If you fail to make the payments set out in your agreement, your car could be repossessed, and your credit rating may be adversely affected

Deposit

• The deposit is the amount you pay upfront at the start of the agreement, and it will determine how much you need to borrow.
• The larger your deposit, the less you’ll have to borrow and the smaller your monthly payments will be.

Monthly Payments

• Once you’ve chosen the term (length) of your agreement, the amount of the monthly repayments will be spread equally across the months and remain fixed throughout your agreement.

End of Contract

• Once you’ve made your final monthly payment, the car is yours to keep or part exchange it for a new car.

---

Personal Contract Purchase (PCP)

Personal Contract Purchase (PCP) is a way to borrow money to buy a car. You pay back the money every month, and at the end of the contract, you can choose to return the car, upgrade, or make one final payment (Optional Final Payment) to own it.

Key features of Personal Contract Purchase

• Monthly payments are kept low as an amount is deferred to the end of the agreement
• Flexible options at the end of a contract – keep, upgrade, or return the car.
  

Risks of Personal Contract Purchase

• Each car comes with an agreed mileage limit which must be kept to, otherwise you will be charged an additional excess mileage charge.
• If your car is damaged beyond regular wear and tear there is a risk of additional charges.
• You do not own the car until you make the final payments at the end of your finance agreement.
• If you fail to make the payments set out in your finance agreement, your car could be repossessed, and your credit rating may be adversely affected.

 

Deposit

• The deposit is the amount you pay upfront at the start of the agreement, and it will determine how much you need to borrow.
• The deposit ranges from 0 to 35% of the vehicle price.
• The larger your deposit, the less you’ll have to borrow and the smaller your monthly payments will be.

Monthly Payments

• Your monthly payments will be fixed throughout your agreement and are affected by the amount of your deposit.
• A Guaranteed Future Value (GFV) is used to determine how much you’ll have to pay at the end of your finance agreement in order to own the car.

Car Usage

• Your PCP agreement will come with rules around car usage that help you avoid any further charges. These will determine how many miles you can drive throughout your agreement.

---

Leasing, Personal Contract Hire (PCH)

Personal Contract Hire is a finance offer that allows you to hire a car for an extended length of time. You pay a fixed monthly fee to hire the vehicle, and throughout the length (term) of the agreement it is your responsibility to take care of it. You do not own the car and you must return it at the end of the agreement.

 

Key features of Personal Contract Hire

• Contracts offer terms between 24 and 48 months.
• You choose how much deposit you put down at the start of the agreement.

Risks of Personal Contract Hire

• You must maintain the car’s condition to meet manufacturer guidelines.
• If you return the car in poor condition, or exceed the agreed mileage limit , you will be charged an additional fee.
• You do not own the car.
• If you fail to make the payments set out in your agreement, your car could be repossessed, and your credit rating may be adversely affected.

Initial Rental

• The Initial Rental is the amount you pay upfront at the start of the agreement.
• The Initial Rental equates to the value of anywhere between 1 to 9 months rentals.

Monthly Rentals

• Your monthly rentals will be fixed throughout your agreement, and they are affected by the size of your Initial Rental.
• Once you’ve chosen the term (length) of your agreement, the rental amounts will be spread equally across the months.
• To help keep the car within the wear and tear guidelines, optional maintenance packages can be added into the monthly rental cost. You will be expected to stick within the pre-agreed mileage limits and if you fail to do so, you will face a fee.

End of Agreement

• Once you’ve made your final monthly rental and your agreement has come to an end, it’s time to return your car to the lender.
• Upon its return, the car will be assessed for wear and tear against the manufacturer guidelines that were shared with you at the start of the agreement.
• If any damage is noted beyond the usual wear and tear, you will face an additional fee.

 

 

 

Insurance

All insurance policies are based on the probability that a certain event will not happen.
The higher the probability is that an event will happen , the higher the  insurance premium.

Example

Bodgit Insurance offer house cover at a premium of £3.50 per £1000.
How much does it cost to cover a £189,000 house  ?

 

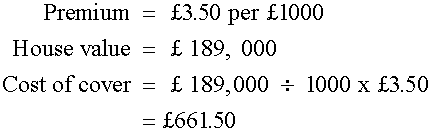
Bank Interest

Interest is a percentage of the capital that is charged on loans/borrowing money and paid on savings.

 

Simple Interest

Simple interest gives you a percentage return based purely on your original capital.

Example

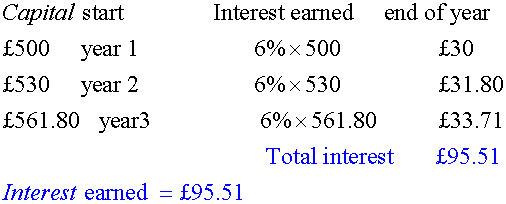
Calculate the simple interest on   £500 for 3 years at 6% per annum.

   

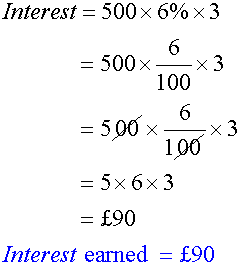
Compound Interest

Compound interest uses the interest earned to increase the capital,
thus increasing interest.

Example

Calculate the compound interest on   £500 for 3 years at 6% per annum.

    

If the interest rate per annum doesn't change, a formula can be used
which is based on the starting value (capital),the increased or reduced interest rate and the term of the calculation.

If the calculation is based  over years, the mnemonic CR^y can be used:-

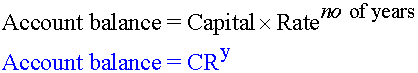
Example

Calculate the compound interest on   £500 for 3 years at 6% per annum.

The mnemonic CR^y can still be used for monthly payments, but remember to convert the term to months:-

Example

Calculate the compound interest on   £500 for 1 year at 0.3% per month.

 

More than one of interest periods

The mnemonic CR^y can be daisywheeled as a chain :

Capital x rate1^{term 1} x rate2 ^{term 2} x rate3 ^{term 3} ....etc.

 

Example

£5,000 is placed in a saving account on 1st April 2022.

No withdrawals are made.

The effective rates of interest are shown:

What is the balance of the account on 31st March 2023 ?

• There are 4 complete months at 0.415% per month. (April,May,June July)
• There are 5 complete months at 3.2% per year (August,September,October,November, December)
• There are 3 complete months at 1.3% per year (January, February, March )

 

 

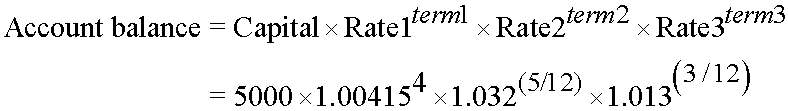
This gives a result of 5167.3349, which is a balance of £ 5167.33

 

 

 

CR^y can also be used to work out a rough APR (Annual Percentage Rate ) :-

Example

What is the APR for a credit card which charges 1.5% interest per month?

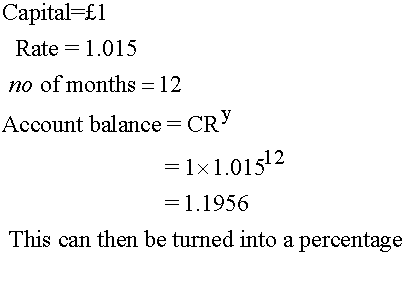
Effective Interest

 This is the actual interest rate on a loan or investment when accounting for the effects of compounding over a specific period.

Effective Interest Rate = (1 + (Nominal Interest Rate / Number of Compounding Periods))^(Number of Compounding Periods) - 1

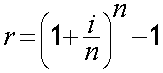
where r is the annual effective rate , i is the nominal interest rate ( the stated or quoted rate ) and n is the number of compounding periods per year.

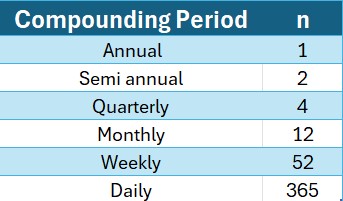
The compounding period is important, since it can affect the amount of money earned or owed.

EAR - Effective Annual Rate
This is the true interest rate on a loan that takes compounding into account.

AER - Annual Equivalent Rate is used for savings or investments.

 

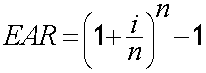
Example

A bank offers a loan with a nominal annual interest rate of 5%.

Find the effective annual rate if the interest is compounded,

1. semi-annually
2. monthly
3. daily

1 . Semi - annually

Here, i = 5% and n = 2

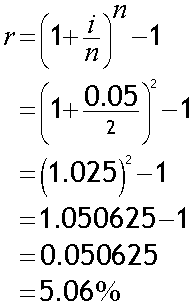
The effective annual rate is 5.06%

 

2. Monthly

Here, i = 5% and n = 12

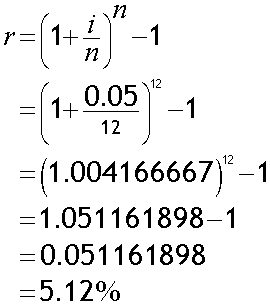
The effective annual rate is 5.12%

3. Daily

Here, i = 5% and n = 365

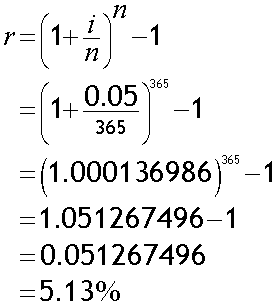
The effective annual rate is 5.13%

 

Changing between effective rate of interest periods

To convert between periods

Let i _new = Converted period interest rate
i _old = Original period interest rate

Cf_old = Original compunding frequency
Cf_new = Converted compunding frequency

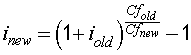
Source LibreTexts Mathematics Equivalent and Effective Interest Rates

 

To convert from an annual effective interst rate to a monthly effective interest rate, use

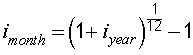
Do NOT just divide by 12!!

Example

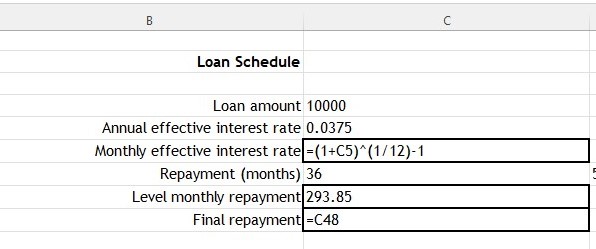
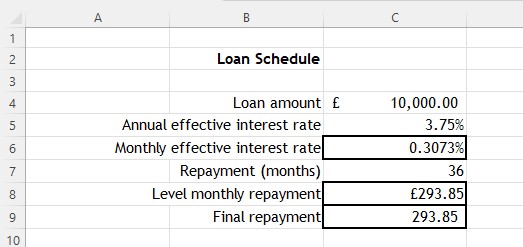
Given an annual effective interest rate of 3.75% , calculate the montly effective interest rate.

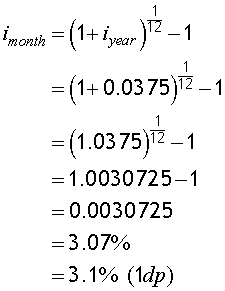
The monthly effective interest rate is 3.1% (1dp)

If using Excel , use the formula

=(1+Cell with annual effective rate )^(1/12)-1

Don't forget the starting equals sign, to show Excel you are inputting a formula.

In the example just given above, the formula entered is

=(1+C5 )^(1/12)-1

 

The monthly effective interest rate is 3.1% (1dp)

Use in Loan Schedules

Example

A loan of £10,000 is borrowed over 3 years. The annual effective interest rate is 7.1%

 

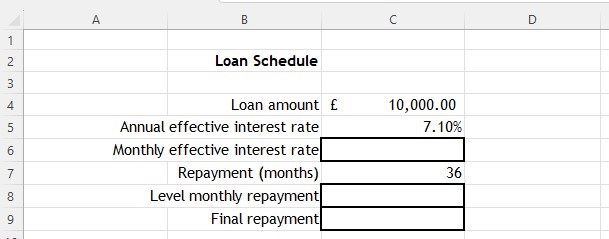
Inserting the formula =(1+C5 )^(1/12)-1 into cell C6 calculates the monthly effective interest rate.

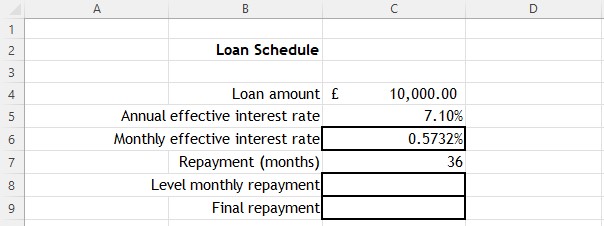
The Excel function PMT calculates payments based on a constant interest rate and number of periods.

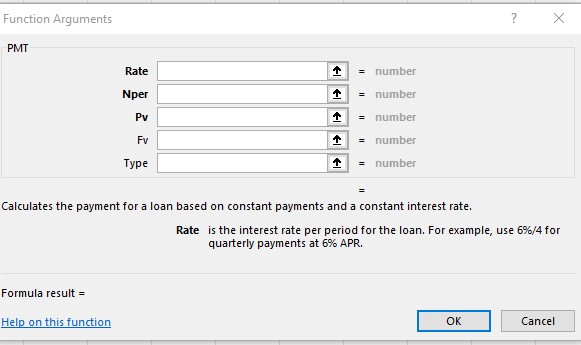
Here,

• the rate is the effective monthly rate, cell C6
• NPER is the number of payments , cell C7
• Pv is the value of the loan, cell C4

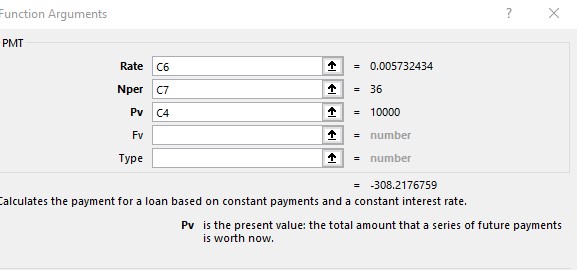
This calculates a fixed monthly payment of £308.22

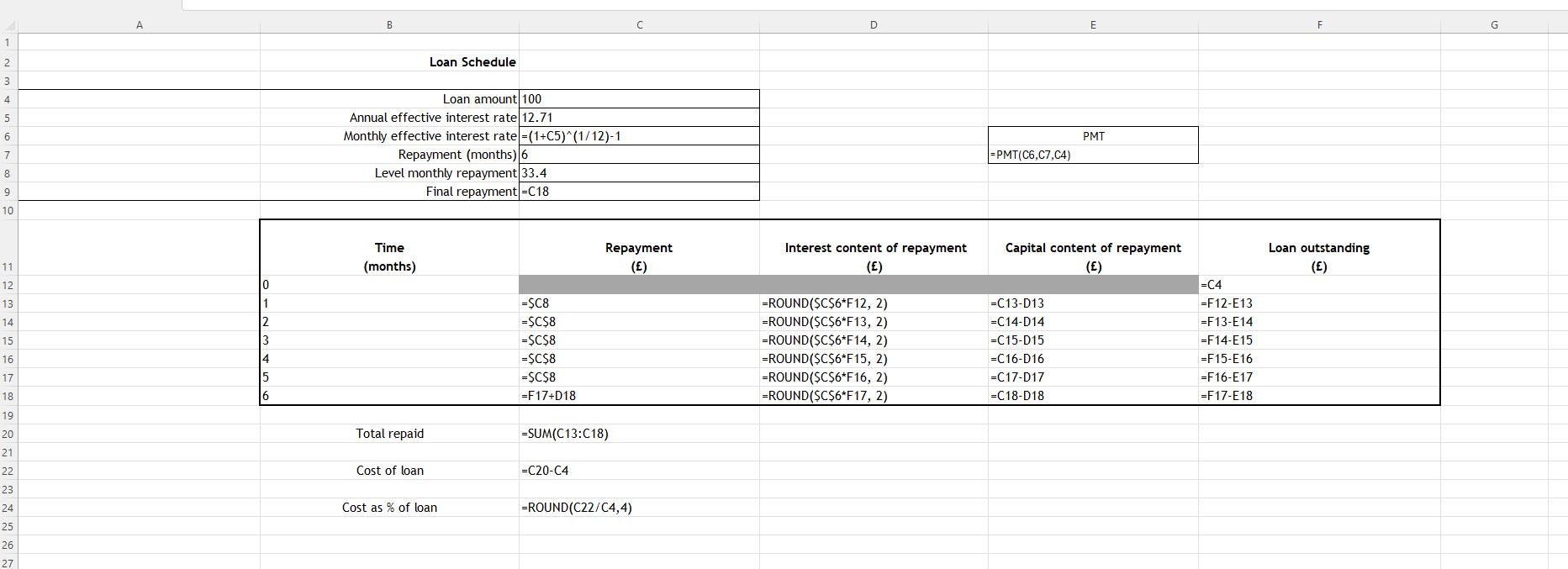
Set up a loan schedule with these headings :

 

Enter =$C$4 into cell F12 (This can be done by entering =C4 and the pressing the F4 button to get the result)

Expand the table down to 36 months

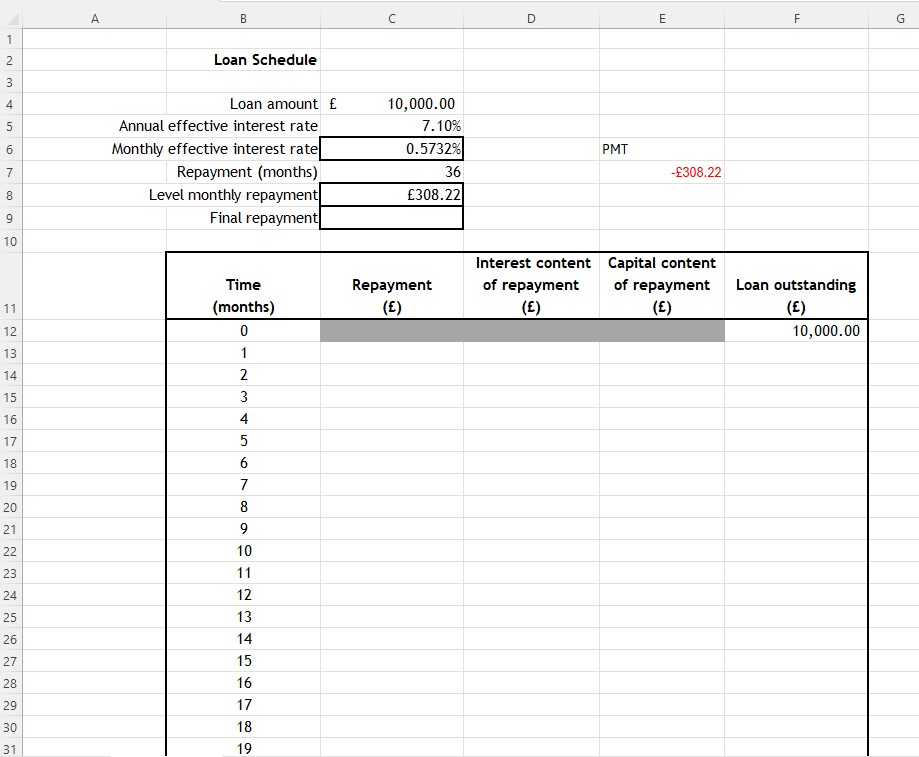
The repayment figure is C8, so enter =$C$8 in cell C13

To get the Interest content of repayment , enter =ROUND($C$6*F12, 2) into cell D13 , this multiplies the outstanding loan by the effective monthly amount of interest and rounds to 2 dp.

The capital content of repayment is the repayment less the amount of interest, so enter =C13-D13 into cell E13

The loan oustanding reduced by the amount of capital repaid, so enter =F12-E13 into cell F13

Copy and paste all the way down to the last column

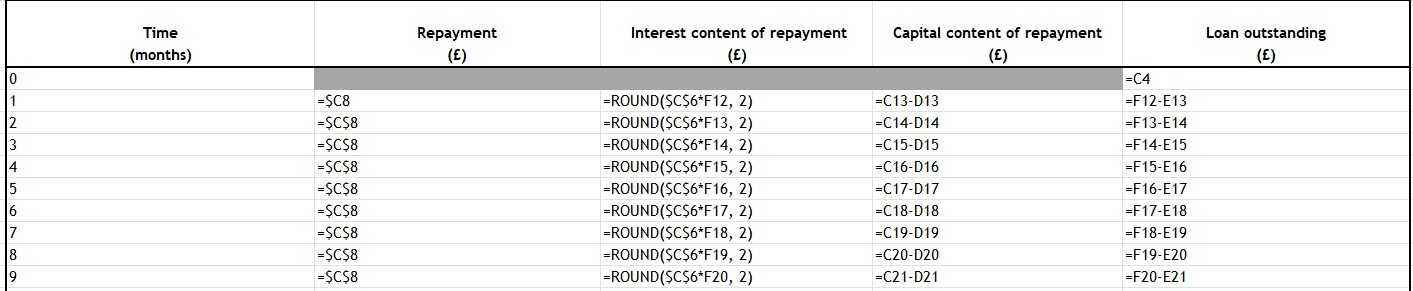
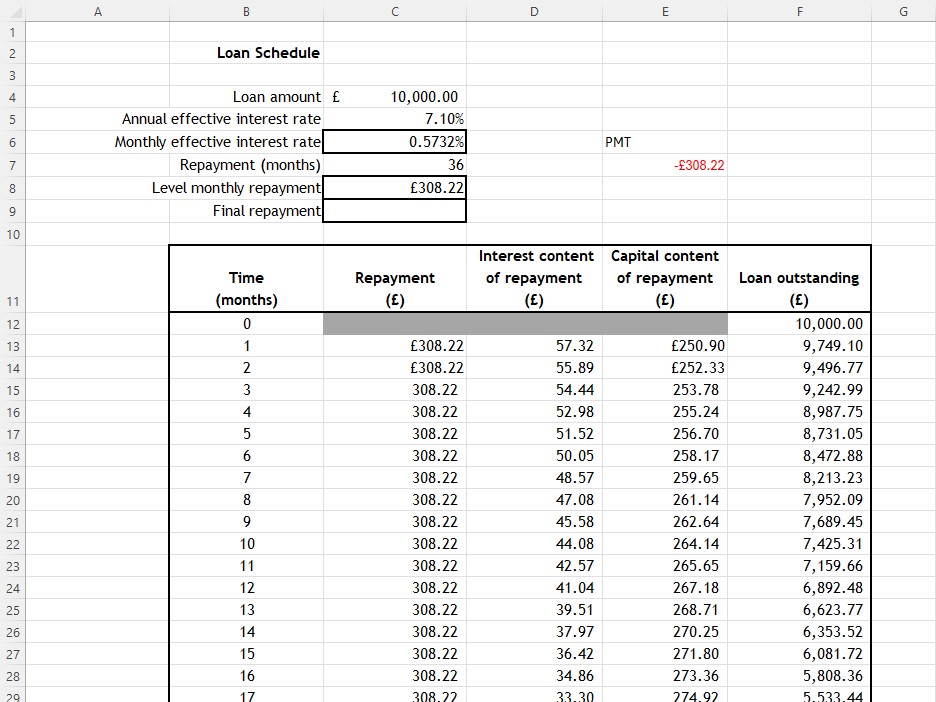
The final payment will differ from the rest.

Enter =F47+D48 into cell C48 , which adds the last interest payment to the outstanding loan.

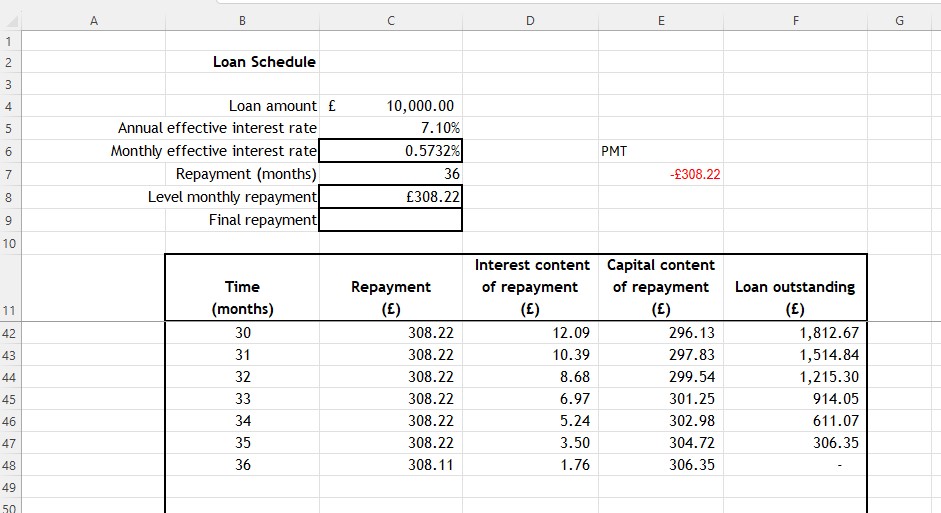
Summary

 

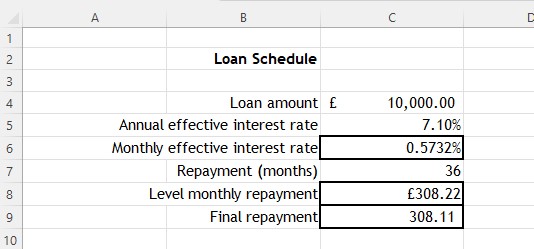
This can be represented by the Recurrence relation
U_n+1 = 1.0057U_n-308.22

From the graph, it can be seen that after 15 months, the outstanding loan is approximately £6,000

 

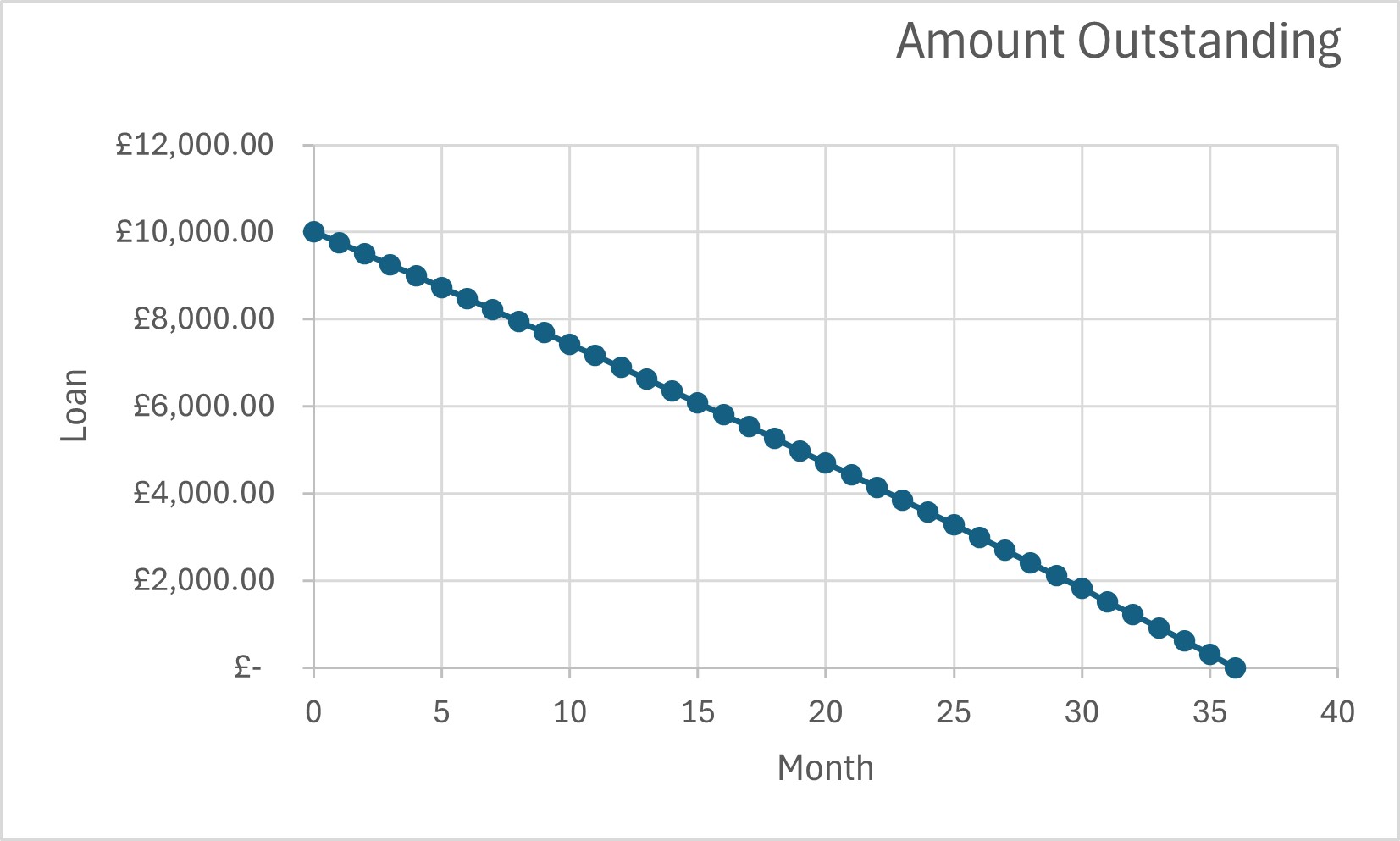
Comparing Loans

The effective monthly rate can be used to quickly compare loan offers.

Example

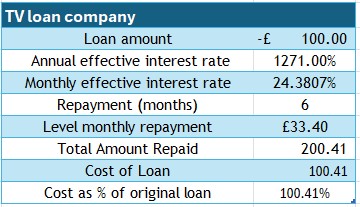
A television commercial advertises a short term loans with a typical annual interest rate of 1271%.

1. Create a loan schedule for a loan of £100 borrowed over 6 months.
2. Calculate the cost of the loan.
3. What is the cost of the loan as a percentage of the original loan ?
4. Comment on your findings

 

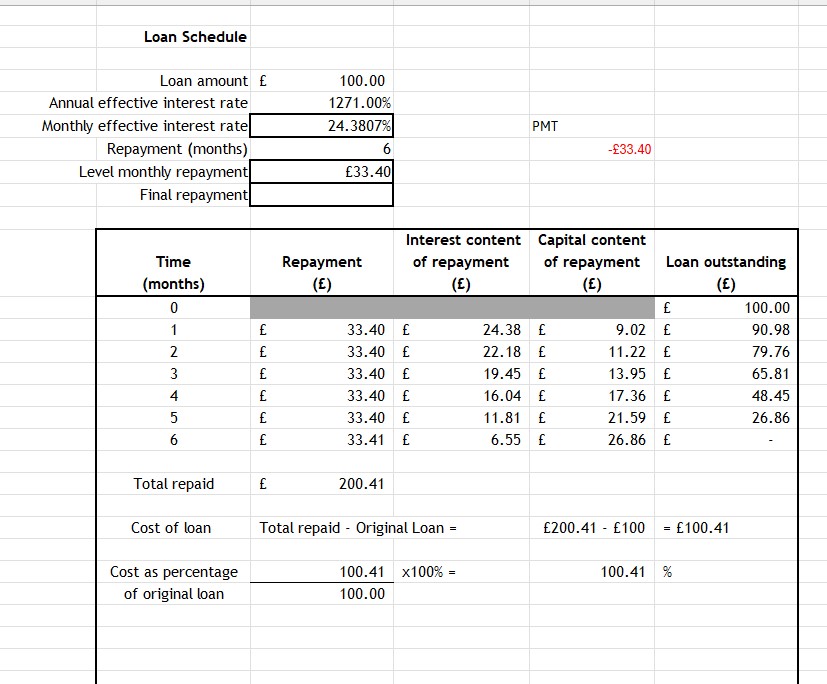
1 . From the loan schedule, the total repaid is £200.41
2 .The cost of the loan is total repaid - original loan , so £200.41 - £100 = £100.41
3. The cost of the loan as a percentage of the original loan is (cost of loan / original loan ) x 100% =(£100.41 / £100 )x 100% = 100.41%

4. The cost of borrowing the money is more than the original loan was!

The data can be summarised :

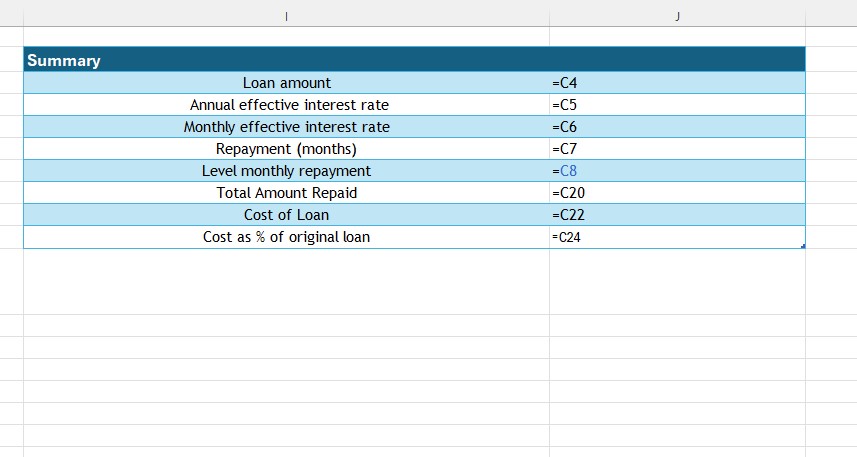
Excel formula view :

Example

£10,000 is required as a loan to be repaid over 3 years.

Three loan providers are compared :(Interest rates sourced July 2025)

• Own Bank : AER 5.6 %
• Internet Bank A : AER 22.9%
• Internet Bank B : AER 99.9%

Complete the loan information box for each bank :

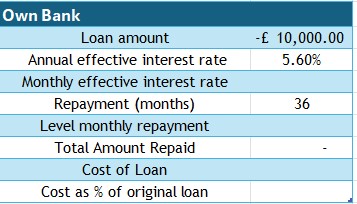
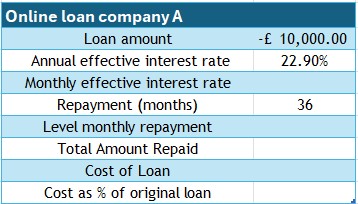
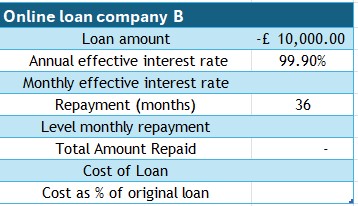
Comment on your findings.

 

 

 

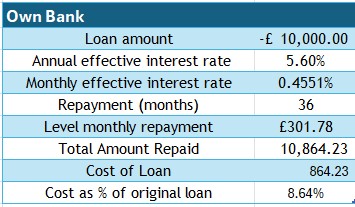
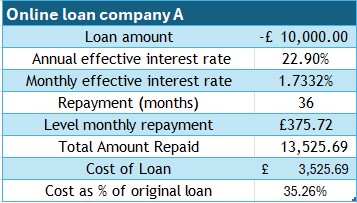
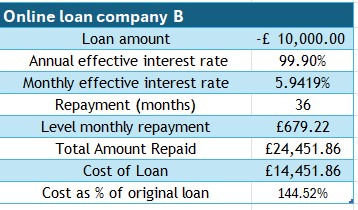
Clearly, the loan from Own Bank is cheapest.
The effective monthly interest of Internet Bank B is more than the annual interest rate for Own Bank!

Nominal interest rate from effective rate of interest

Working backwards

If given an EAR , or AER, the nominal interest rate can be found by changing the subject of the formula from r to i.

so

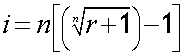
where i is the nominal interest rate ( the stated or quoted rate ) , r is the annual effective rate and n is the number of compounding periods per year.

Example

What is the annual nominal interest rate for a loan with an EAR of 9% compounded monthly ?

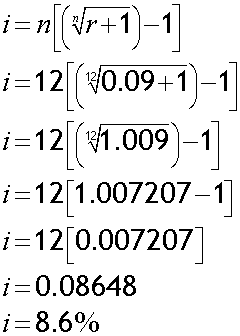
Alternatively,

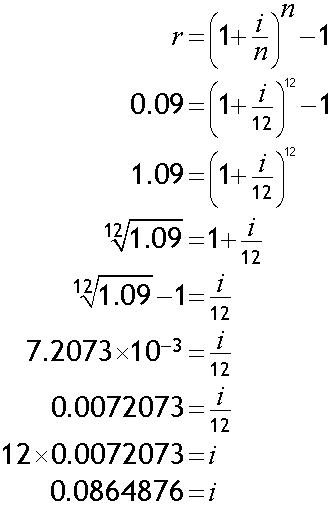
The annual nominal rate is 8.6% (1 dp)

 

Example

An online internet bank offers loans with an annual rate of 61.94% .

Calculate the effective monthly rate.

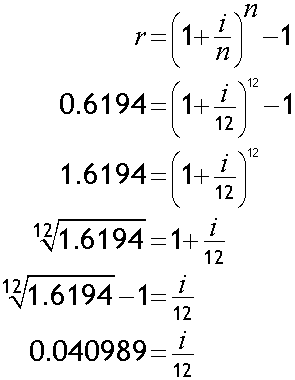
The effective monthly rate is 4.1 % (1d.p.)

Alternatively,

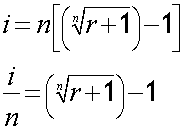
so for monthly terms

 

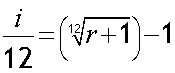
substituting data

 

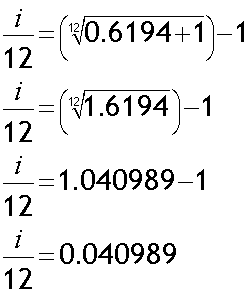
The effective monthly rate is 4.1 % (1d.p.)

 

 

 

 

 

 

 

APR ( Annual Percentage Rate )

This is the interest rate paid each year on an outstanding loan amount.

It includes charges and fees - but does not include compounding.

 

 

 

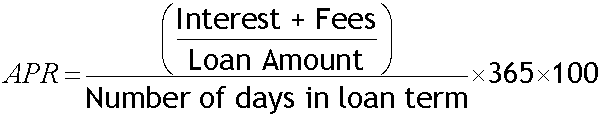
Foreign Exchange

Exchange rates

Converting currency is a form of applied ratio.

Converting into another currency

Examples

Fred wishes to convert £150 into US dollars.
The exchange rate is £1 = $1.67, with no commission.
How many dollars does he get ?

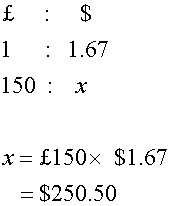
No. of dollars =£150 x $ 1.67 = $250.50

 

Using the rule of 3

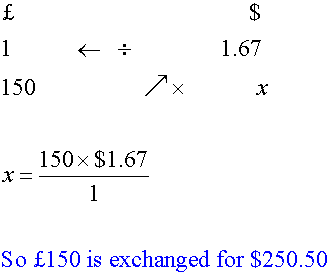
Converting back

Fred wishes to convert $75 back into pounds sterling.
The exchange rate is still £1 = $1.67,  with no commission.
How much  does he get ?

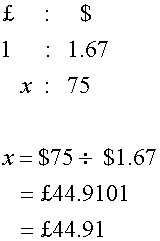
Amount of pounds sterling =$ 75 ÷ $150 = £ 44.91

Using the rule of 3

 

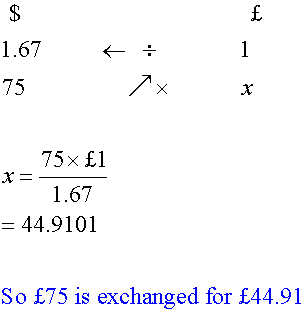
When Joe converts  $150 into Euros, he receives € 108.09
There was  no commission.  What was the exchange rate ?

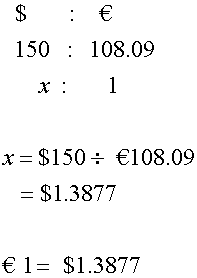
or