Graphs of Exponential and Log functions

Exponential functions

           y = a^x

An ordinary exponential function always has the points
    (0, 1) , (  1 , base) and (-1, 1/base ) 
      since     a⁰ =1 ,   a¹ = a  and a^-1 =1/a  

    

The x axis is an asymptote , the graph never crosses the x –axis.

When the base is greater than 1

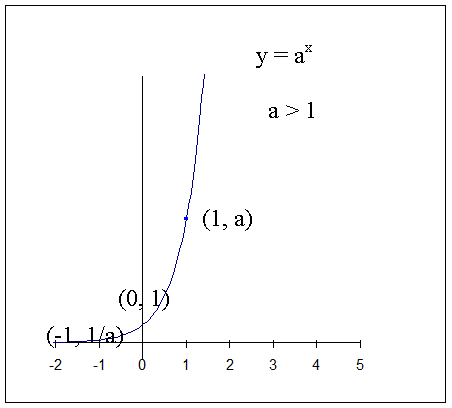
And when the base is smaller than 1

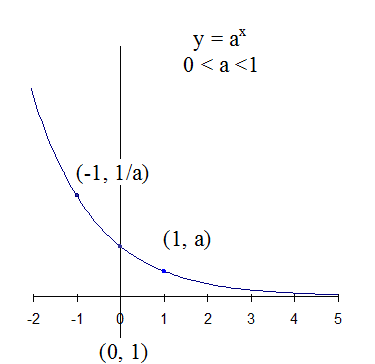
Example

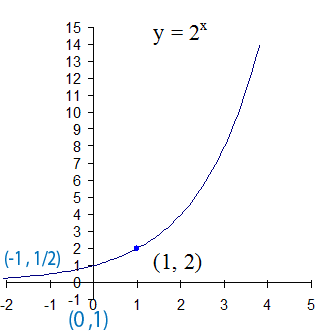
To calculate the values of y , raise x to the power of the base.

y = 2^x  

Table of values

 

Logarithmic functions

An ordinary log function always has the points
(1, 0)   and (base, 1)
since
log_a1=0 and loga_a=1

The y axis is an asymptote , the graph never crosses the y –axis.

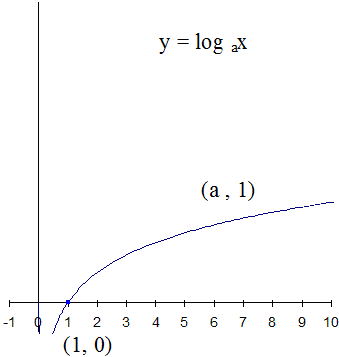
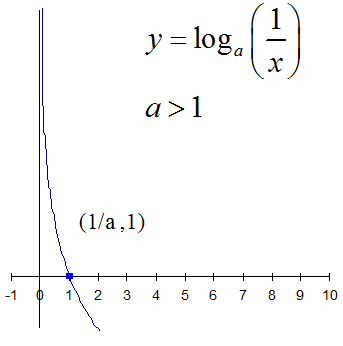
Example

 

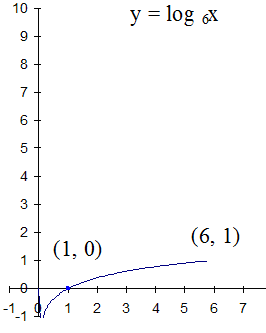
To calculate the values of y ,

If   y = a^x
x = log_a y

Shifting log graphs left and right

Take the graph y=logx

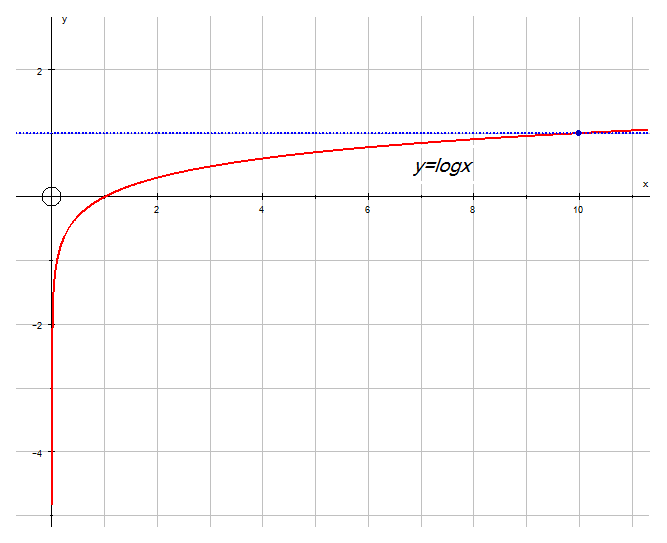
Here, the base is 10.
Look for the points ( 1,0) and (10,1)

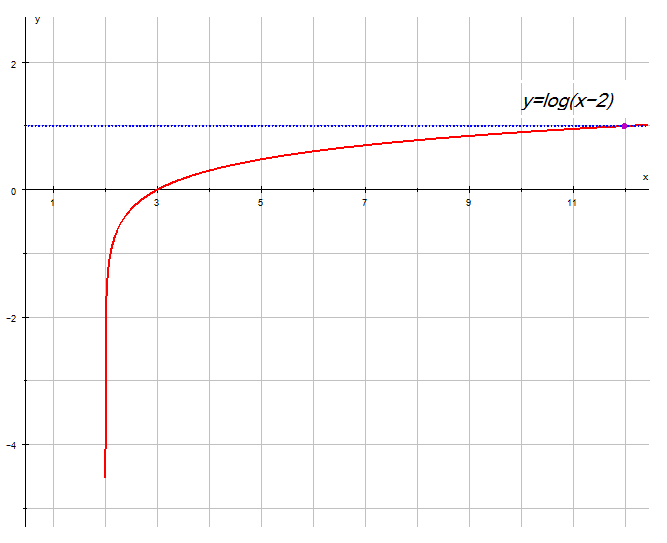
Now take the graphs y=log(x+2) and y=log(x-2)

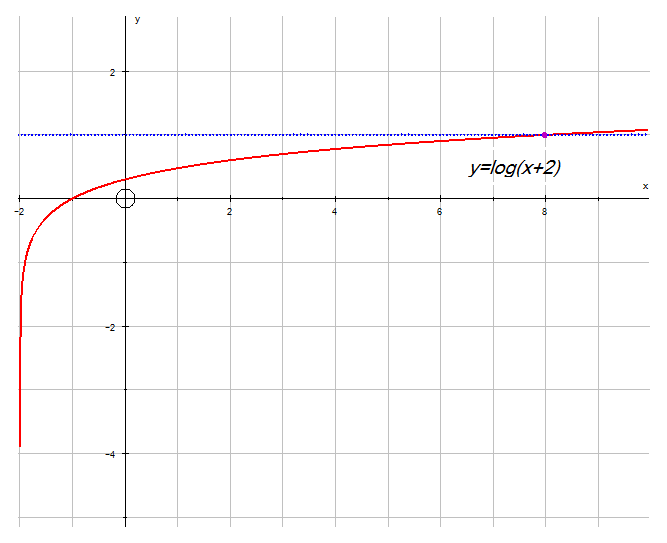
Note how they shift the opposite way !

Shifting up and down

Again, the base is 10.
Look for the points ( 1,0) and (10,1)

 

• Now shift upwards

 

 

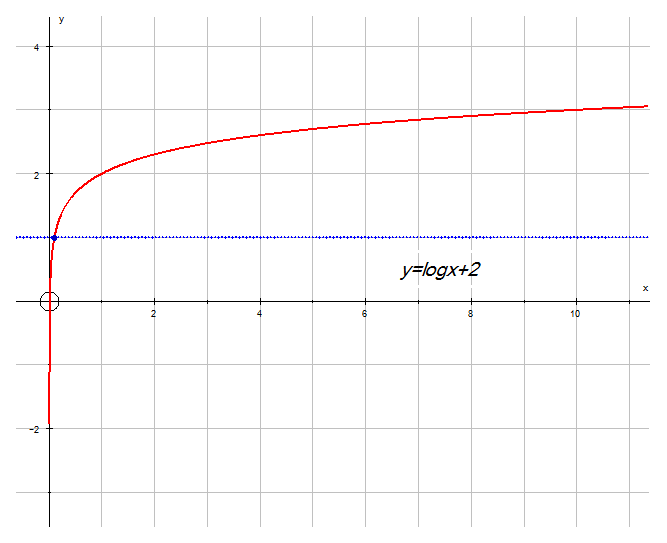
 ( 1,0) has moved to ( 1, 2)  and (10,1) has moved to (10,3)

 

• And downwards

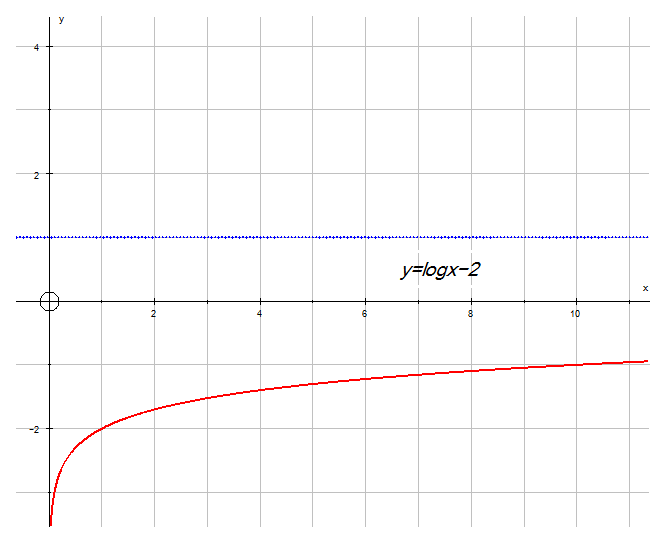
( 1,0) has moved to ( 1, -2)  and (10,1) has moved to (10,-1)

 

Bringing it all together

 

The graph below has equation y=log(x+a) +b.
Find the values of the integers a and b.
Write down the equation of the graph.

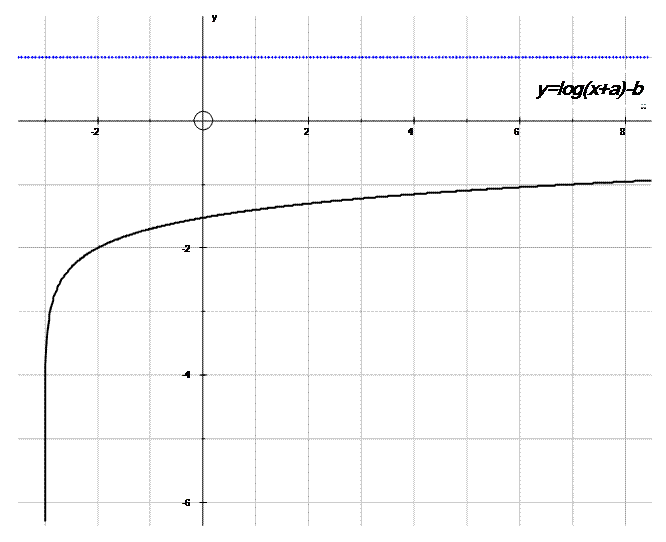
First, notice that there is an  asymptote at x=-3.
The graph has shifted to the left three spaces.
This means that a must be 3.

so    y=log(x+3) +b.

The base is 10, since there is no subscript on the log.
This means that the point (10,1) would normally exist.

However, this has moved to the left three spaces, so
expect the point (7,1)

On the graph, when x=7 , y = -1.
This means the graph has moved down two spaces.
b must equal -2.

so  a = 3 , b =-2
and   y=log(x+3) –2