Systems of Equations

Solving simultaneous equations can be done quite easily by elimination.
However, they can also be solved by using matrices.

Example

ax +by = e
cx + dy = f

can be represented by

Ax=b

Where

 

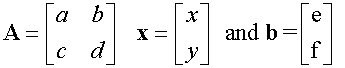
so ( using parenthesis now)

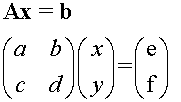
This can be further shortened to the
augmented matrix form by combining A and b

 

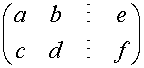
Which then allows Elementary Row Operations to be used,
to reduce the equations to upper triangular form.

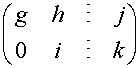
or to continue and solve

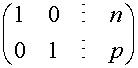
Reforming the matrix then gives

 

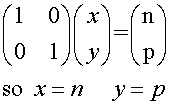
Elementary Row Operations

• The order of equations can be switched.
• An equation can be multiplied by a constant.
• Equations can be added or subtracted.

 

Example

2x +3y = 7
3x + 4y = 6

can be represented by

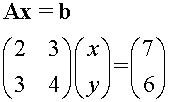
Augmented form

 

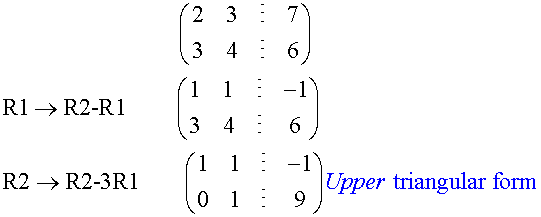
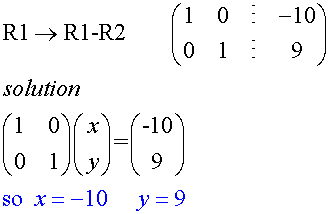
Gaussian elimination

 The system of equations

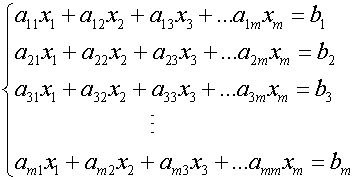
can be written in the form
Ax=b

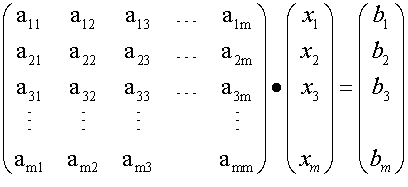
or in augmented form

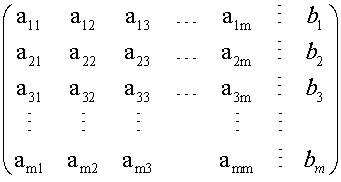
The  process of reducing a system of equations
to upper triangular form, then back substituting to solve,
is called Gaussian elimination.

 

A redundant row indicates the lack of a unique solution,
a general solution exists.

An inconsistent row indicates that no solution exists.

Small changes in the coefficients leading to large changes
in the solution indicate an ill-conditioned system.

 

Example

Solve the system of equations

x +2y +z = 14
3x - y - 4z = 7
-x + y +3z = 2

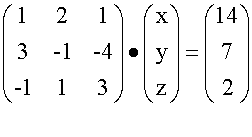
In augmented form

 

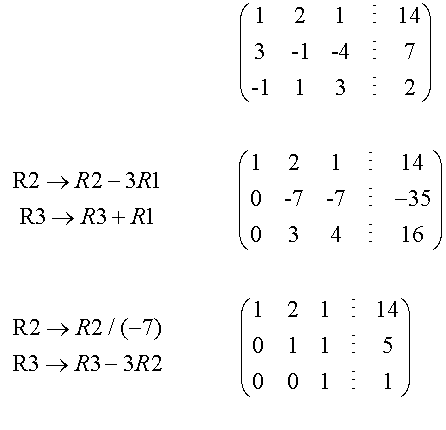
At this stage, back filling can take place.
Row 3 gives z =1
Row 2 is    y + z = 5 ,   so   y +1 = 5,  i.e. y = 4
Row 1 gives x +2y +z = 14,
so x + 2x4 + 1 = 14   giving x = 5

Alternatively, the matrix can be continued.

 

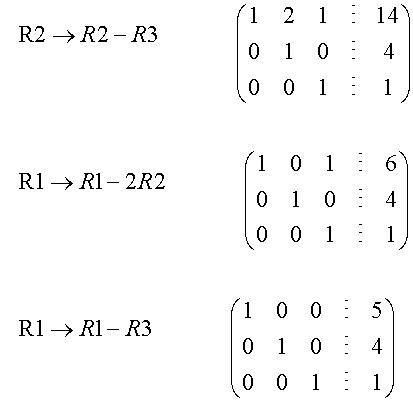
        Solution

     

 

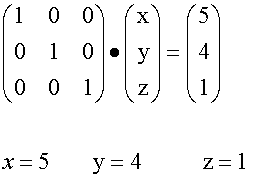
Example

Solve the system of equations

2x + y - 2z = 5
3x + 2y + 5z = 5
4x + 2y - 4z = 10

 

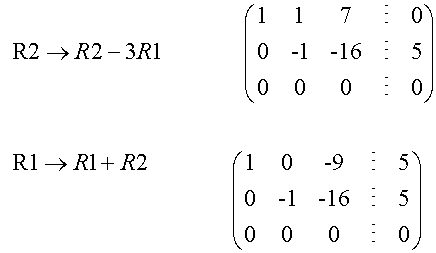
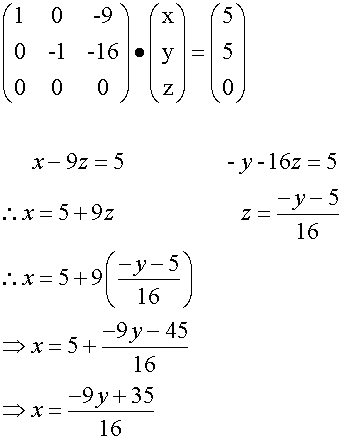
 Click for a  spreadsheet to calculate a 3x3 system

 Gaussian elimination can be used to find the inverse of a matrix.