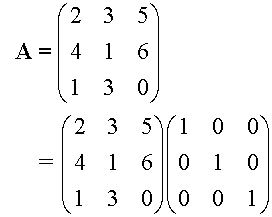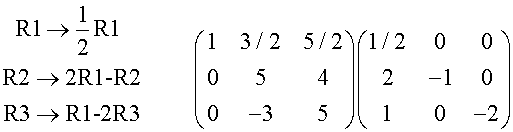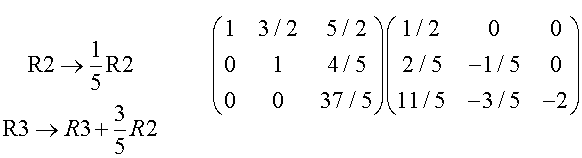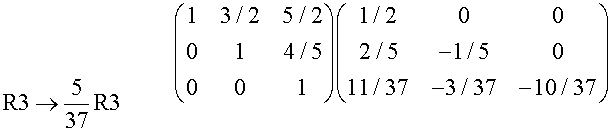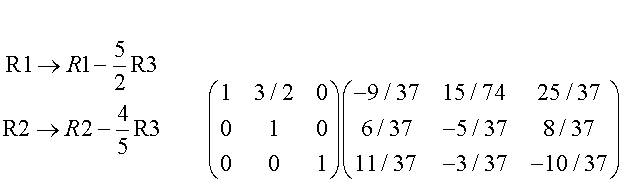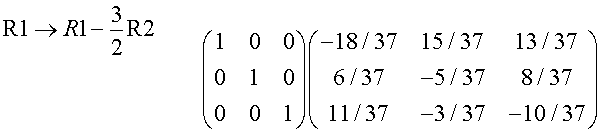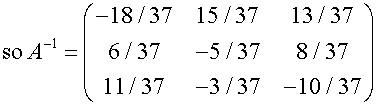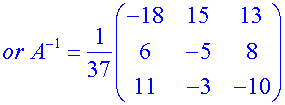Determinants
Solving simultaneous equations can be done quite easily by elimination.
However, what happens if substitution is investigated ?
Solving the equations
ax +by = e
cx + dy = f
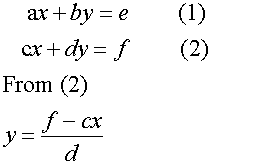
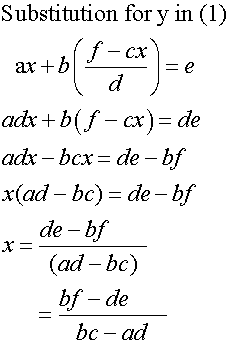
Note, the numerator is found by cross multiplying
and subtracting using the y co-efficients.
bf de
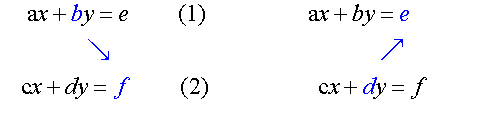
The denominator is found by reverse cross multiplying
and subtracting the coefficients of x and y.
bc ad
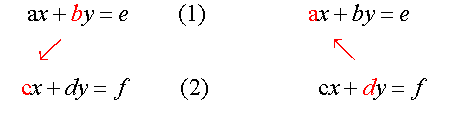
And, for y
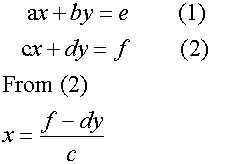
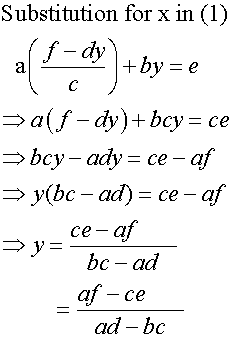
Note, the numerator is found by cross multiplying
and subtracting using the x co-efficients.
af ce
The denominator is found by cross multiplying
and subtracting the coefficients of x and y.
ad bc
This is the vedic way of solving simultaneous equations.
It will only work when ad – bc ≠ 0
Example, solve the following system of equations
2x +3y = 7
3x + 4y = 6
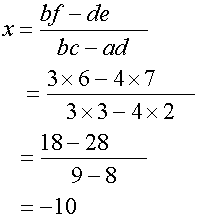
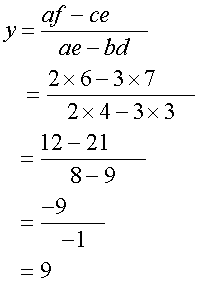
Cramer's Rule
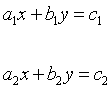
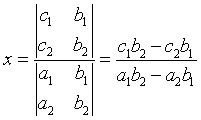
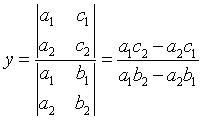
Example, solve the following system of equations
2x +3y = 7
3x + 4y = 6
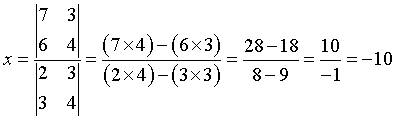
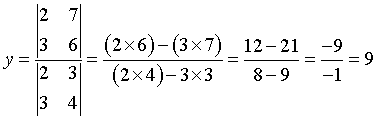
Click for a spreadsheet to calculate a 2x2 system.
Determinants
The system of equations
ax + by = e
cx + dy = f
can be written in matrix form as
Ax = b
Where
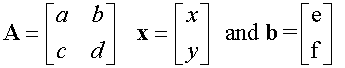
Notice that the denominator from above,
ad – bc , is found by cross multiplying and subtracting
the elements in A.
This is known as the determinant of A.
It is written det(A) or ![]()
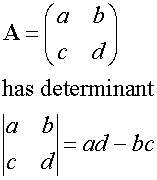
If det(A) = 0, the system has no solution.
Examples
Does the follow system of equations
have a solution ?
3x + 2y = 7
9x + 6y = 6
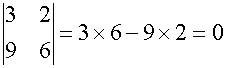
No solution, since determinant = 0
Determinant of a 3x3 matrix
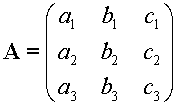
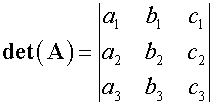
Each element in A is associated with its minor
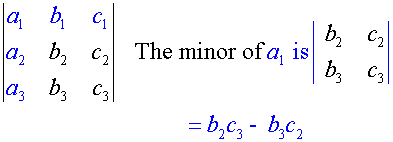
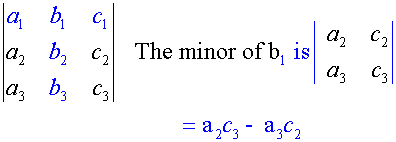
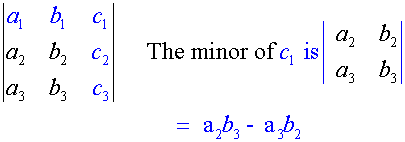
To find the determinant,
- write down each element from the top row.
- Multiply it by its minor.
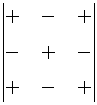
- Add or subtract alternatively according to its position
Place signs
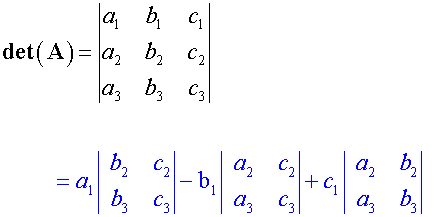
Example
Find the determinant of
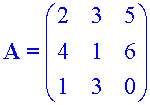
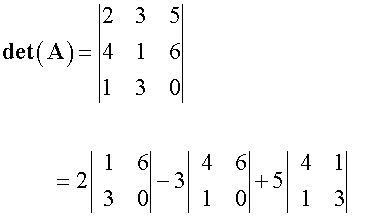
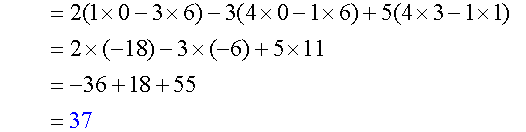
Note:
![]()
Cofactors
Cofactors are minors with their place sign.
Example
Find the cofactors of
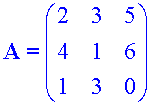 which has
which has 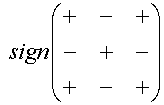
First row
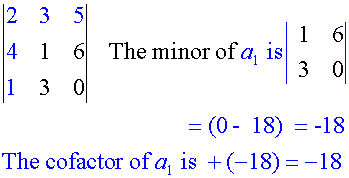
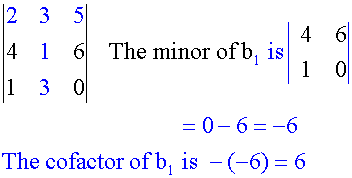
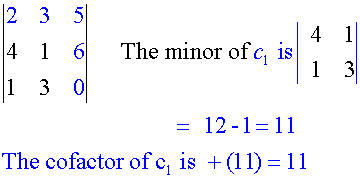
Second row
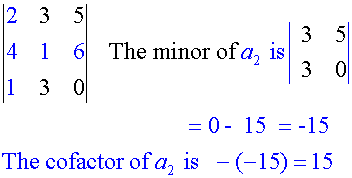
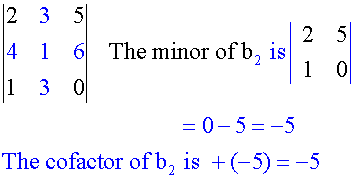
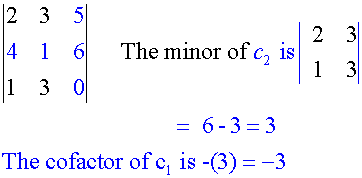
Third row
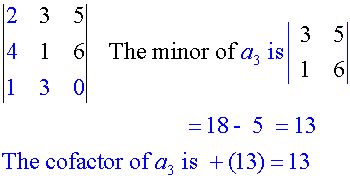
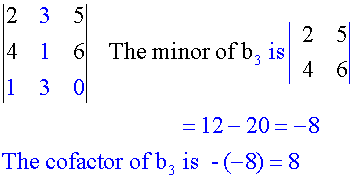
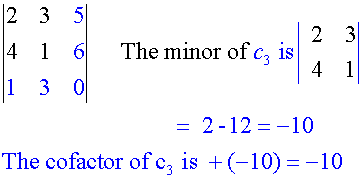
Combining these with the will give a new matrix C,
made up of the cofactors of A.
so 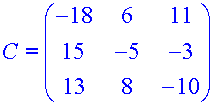
The Adjoint of A
This is written Adj (A)
It is the transpose of C
so
Adj(A) = CT
Example
Find Adj (A) for the matrix
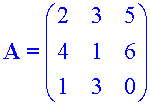
From the work above,
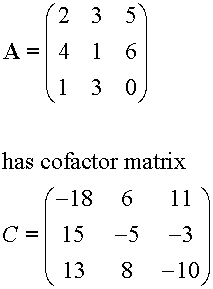
Transposed,
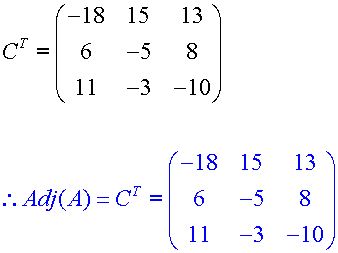
Inverse of a square matrix
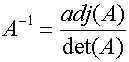
Example
Find the inverse of the matrix
From the work above,
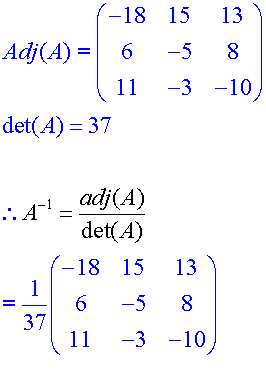
Note,
![]()
Product of a square matrix and its inverse
![]()
Example, using the matrix from above
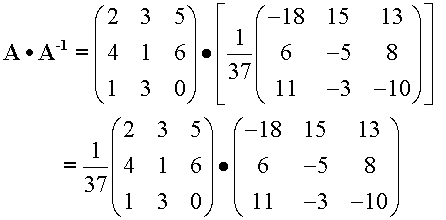
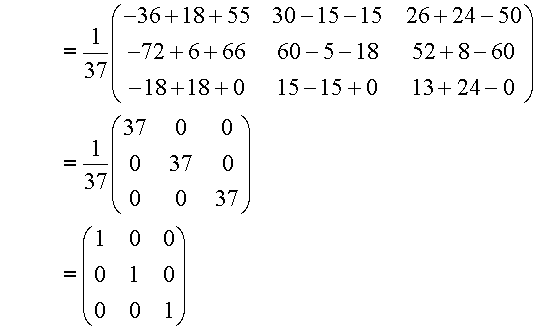
This means that Gaussian elimination can be used to find the inverse:
Write down the matrix to be inverted with the Identity matrix next to it.
Perform ERO’s to reduce the left hand matrix to I,
simultaneously performing the same ERO’s on the Identity matrix.
The result is the inverse of the given matrix.
Example – using the question given above.