Matrices

A matrix is a rectangular array of elements (real or complex numbers) arranged in rows and columns. The array is enclosed within box brackets or parentheses.

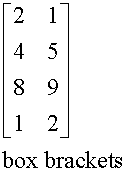
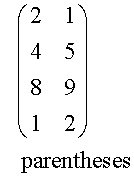
A matrix with m rows and n columns is called an  m by n or  m x n  matrix.
This is also called its order.

If m=n, the matrix is called a square matrix.
If m=1, the matrix is called a row matrix, or row vector.
If n=1, the matrix is called a column matrix, or column vector.

 

Examples

     

  

         

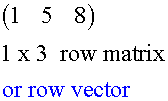
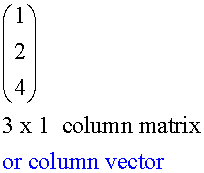
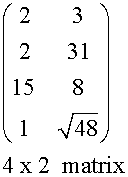
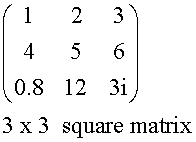
Elements

Each element in a matrix is addressed by its
row and column as double suffixes.
a_ij denotes the element in the i^th row and j^th column.

The elements of an m x n matrix:

 

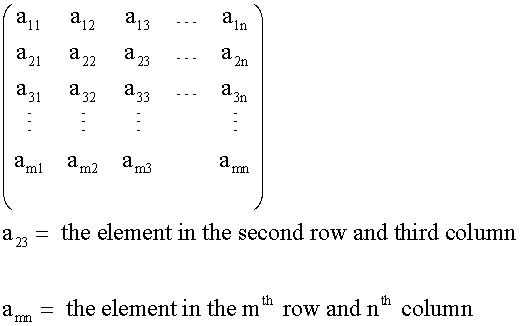
Example

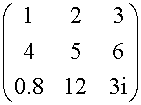
 a₁₃=3     a₂₁=4     a₃₄ does not exist 

 

Matrix notation

An  m x n matrix is often denoted by a capital letter in bold.
In written work, a wavy line is drawn under the capital letter.
It can also be denoted by a general element enclosed in brackets.

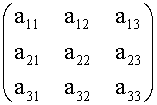
Can be denoted as   A ,  , (a_ij)  or (a)

A row or column matrix is often denoted by a lowercase letter in bold.

  can be denoted as y ,  , (y_j)  or (y)

 

Equality

Two matrices are equal only if they are of the same order and contain corresponding elements.

Examples

 

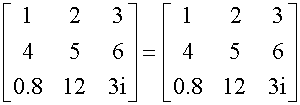
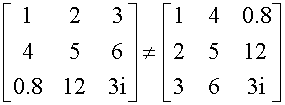
Matrix Addition & Subtraction

Only matrices of the same order can be added or subtracted.
Each element is added or subtracted to its corresponding element.
Matrix addition is commutative   

 

Example

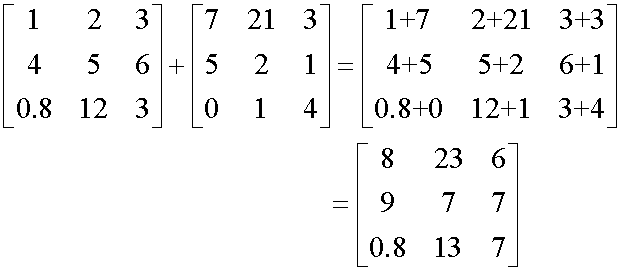
Example

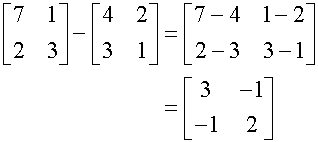
Example

 

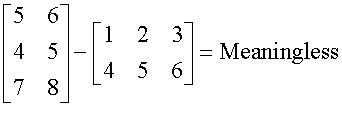
Scalar Matrix Multiplication

To multiply a matrix by a scalar, multiply each element by the scalar.

Example

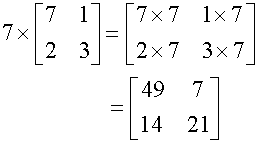
Matrix Multiplication

 This can only be done if the number of columns in the first matrix is equal to the number of rows in the second.

i.e.    If A is an m x n matrix and B is as n x p matrix
then the product   A.B is possible  but B.A  is not possible.

Let B be an m x n matrix and A be an n x p matrix.

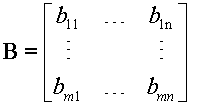
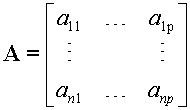
B.A is possible, A.B is not possible

Let the product  BA=C

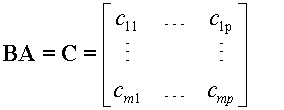
 C is defined

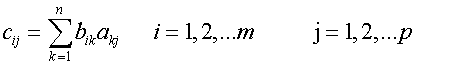
or

 

Matrix multiplication could be described as finding the scalar product of each row in the first matrix by each column in the second.

Example

Let

 

       

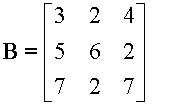
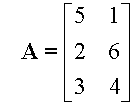
B is a 3x3 matrix        A is a 3x2 matrix
so B.A is possible.

A.B is not possible, so multiplication here is not commutative.

     

 

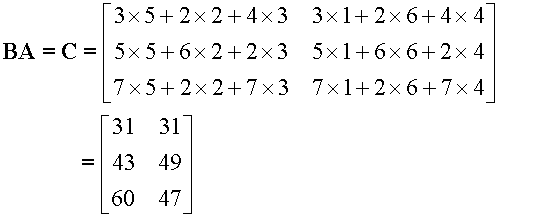
Note

The product of an m x n matrix with an n x p matrix
is a matrix with order m x p

In the product B.A
A is pre-multiplied by B
B is post-multiplied by A

Matrix multiplication is associative

and distributive

provided B and C have the same order and that
the number of columns in A equals the number
of rows in B and C.

Transpose

The transpose of a matrix  A is written A’ or A^T
It is found by interchanging the rows and columns, so that
a’_ij = a_ji

 

Example

 

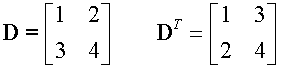
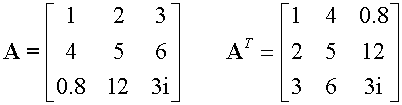
Notice that the leading diagonal remains the same

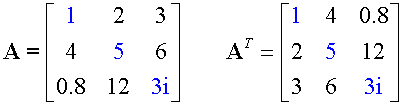
and that the other entries have been flipped.

 

Note

 

Special matrices

A square matrix  is symmetric if a_ij = a_ij

Example

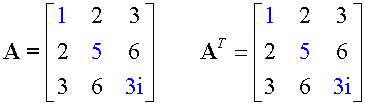
A symmetric matrix has transpose A^T =A

A square matrix  is skew-symmetric if A^T =-A

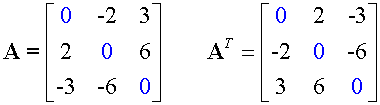
Notice that the leading diagonal is zero

 

A Diagonal matrix  is a square matrix whose
non leading diagonal elements are zeroes.

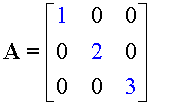
The Unit or Identity matrix  is a diagonal matrix whose
leading diagonal elements are all ones.
It is called I.

   

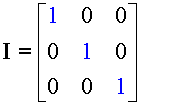
The Null or Zero matrix  is a matrix made purely from zeroes.
It is called 0.

 

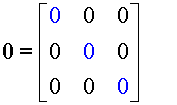
Unlike in ordinary algebra,
A.B = 0 does not allow the assumption that
either A or B is zero.

Example

 

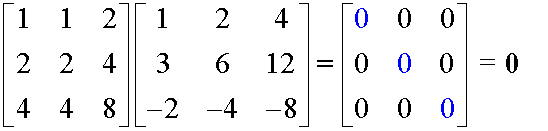
Transformation Matrices

Linear transformations can be described by a mapping
such that T maps the points (x,y) to (x’,y’)

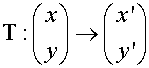
or    

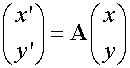
where A (an mxn matrix)
is called the transformation matrix of T.

 

T:x’ = ax + by, y’ = cx + dy can be written

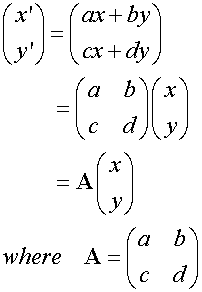
Example

Find the images of the points  A(1,2) , B(3,4) and C(5,6)
after it is translated by the matrix

 

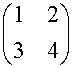
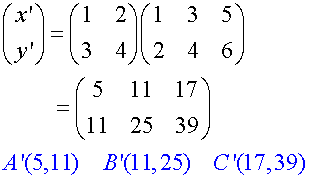
Reflections

Reflection in x axis

 

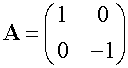
Reflection in y axis

 

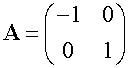
Reflection in line y=x

 

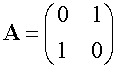
Reflection in line y=-x

 

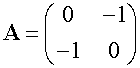
Rotations

Rotation 90^◦ anticlockwise about the origin.

 

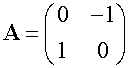
Rotation 180^◦ about the origin.

 

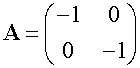
Rotation 90^◦clockwise about the origin.

  

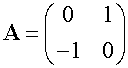
Rotation θ  anticlockwise about the origin.

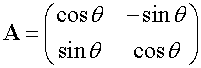
x’ = xcosθ – ysinθ   y’= xsinθ + ycosθ

 

Enlargement with scale factor

 

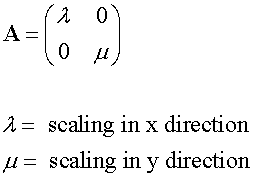
Example : scale factor 2

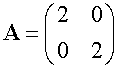
Example : scale factor 1/2

 

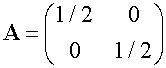
To undo the effects of a transformation,
premultiply the image vector by the inverse of the
transformation matrix.

 

If the inverse of the transformation matrix
equals its transpose, then the transformation matrix
is orthogonal.

If  a point is transformed to its own image, it is called invariant.