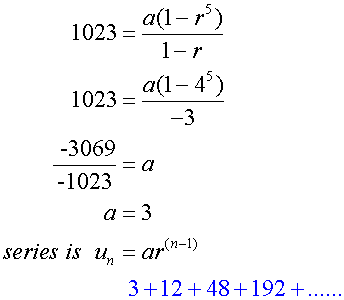Sequences and Series

Refresher

   2,3,4,5,6,…, n 
is  the sequence created by the rule n + 1

u_n denotes the n^th term of the sequence
so  here, u₁= 2, u₂= 3   etc.

Recurrence relations

A sequence can be formed by a recurrence relation.

A first-order linear recurrence relation is of the form

  
, where r and d are constants.

A series is a sum formed by the terms of a sequence.

Example

Find the first-order linear recurrence relation
given by the sequence  2, 4, 10, 28

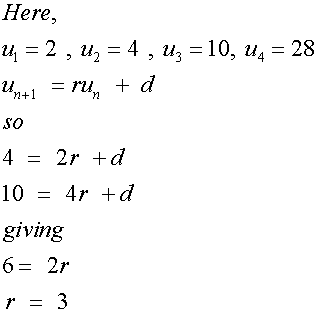
Substituting back ,

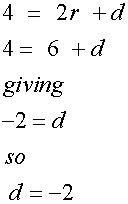
Thus giving the first-order linear recurrence relation
u_n+1 =3u_n -2   

 

Fixed Points

If the relation from above is used with a starting value of

u₁=1, then the following sequence is generated:-

1,1,1,1,……….1   and so on.

Such repetition is called  a fixed point.

u₁=0 generates the sequence

-2,-8,-26 etc.

Since u₁=0 and u₁=2 generate sequences which diverge from 1,
u_n=1 is an unstable fixed point of the relation

u_n+1 =3u_n -2   

 

A stable fixed point occurs when the other sequences converge
to the fixed point.

 

In general

u_n+1 = ru_n + d    has a fixed point when u_n+1 = u_n 
  

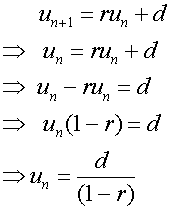
For a stable fixed point

 

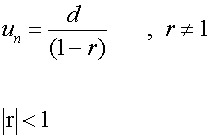
A stable fixed point is often called a limit.

 

Arithmetic sequences

An arithmetic sequence is of the form

u_n+3 - u_n+2 =  u_n+2- u_n+1  =  u_n+1 - u_n= d

The common difference,  d, is a constant.

The n^th term of an arithmetic sequence can  be described

 where a = u₁, d = common difference and n = n^th term

Examples

Find the n^th term of the arithmetic sequence
13,16,19…

Solution:

a=13 , d = 16-13 = 3

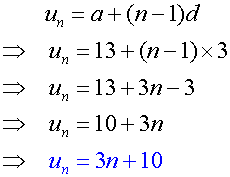
Find the 219^th term of the arithmetic sequence
13,16,19…

From above,

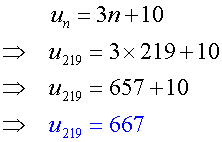
Find the arithmetic sequence which includes
u₇ =33  and u₁₈=88

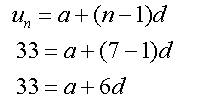and

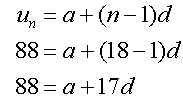
so

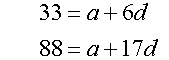
solving simultaneously gives

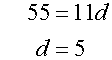
substiting

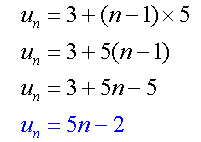
Given the arithmetic sequence
12,22,32,42,52….
find the value of n for which u_n =162 

 

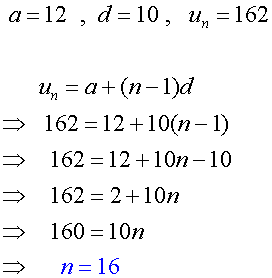
Sum to n terms of an arithmetic sequence

Proof

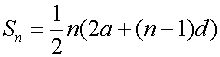
Example

Find the sum of the first 20 terms of the
arithmetic sequence which starts
12,22,32,42,52….

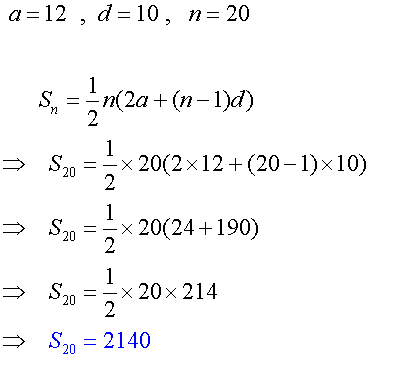
Examples

Find the value of n  of the following
arithmetic sequence such that its sum
first exceeds 250.

12,22,32,42,52….

 

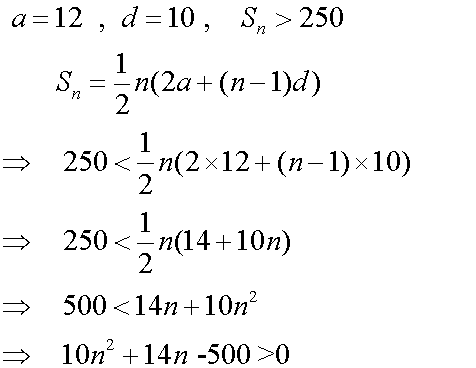
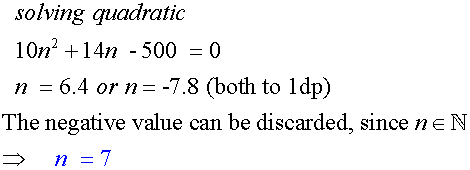
An arithmetic sequence exists such that
the sum of its first 6 terms is 93 and
the sum of its first 9 terms is 207.
Find the sum of its first 4 terms.

 

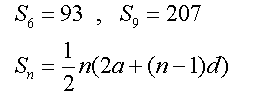
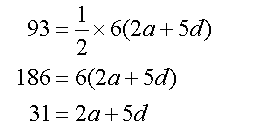
and

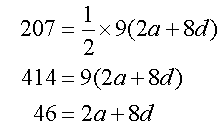
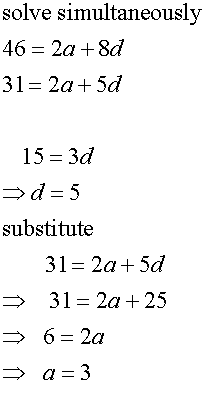
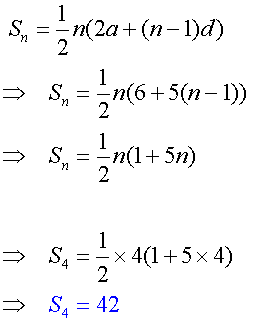
When u_n is given, the following formula can be used:-

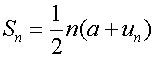
since

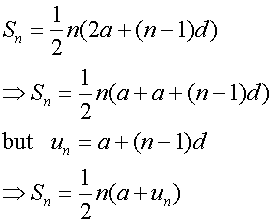
Example

Find the sum of the first six terms of the
arithmetic sequence which starts 3,8,13…
given u₆=28

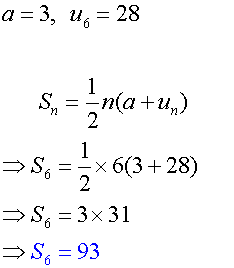
Geometric sequences

A geometric sequence is of the form

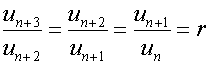
The common ratio,  r, is a constant.

The n^th term of a geometric sequence can  be described

where a = u₁, r = common ratio and n = n^th term

Example

Find the 12^th term of the geometric sequence
5,20,80…

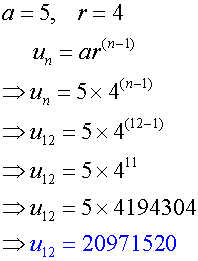
Example

Given the geometric sequence
5,20,80,…..
find the value of n for which u_n = 327680

 

 

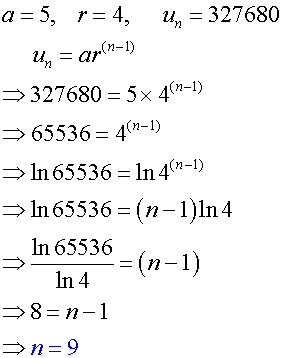
Example

Given u₅=1280 and u₈=81920 ,
find the geometric sequence.

 

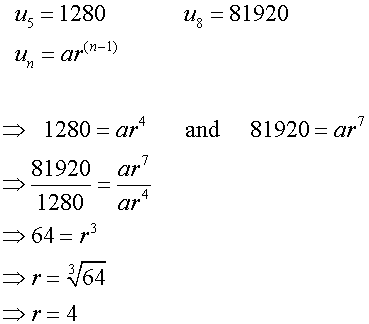
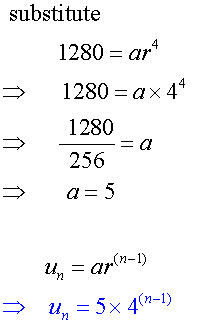
Sum to n terms of a geometric sequence

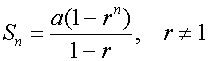
Example

Find the sum of the first seven terms of the geometric sequence
5,20,80…

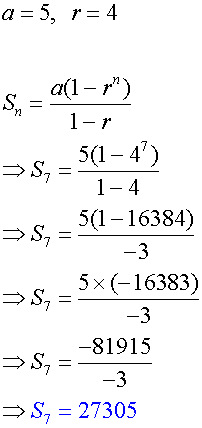
Example

Given S₅=1023 and S₈=65535 , find the geometric series.

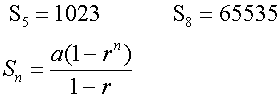
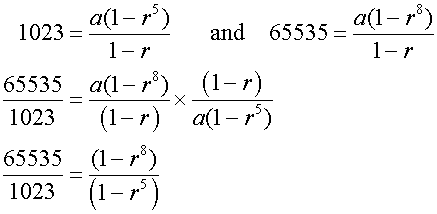
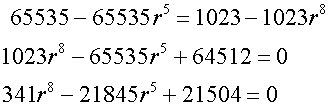
Factorising

Synthetic Division

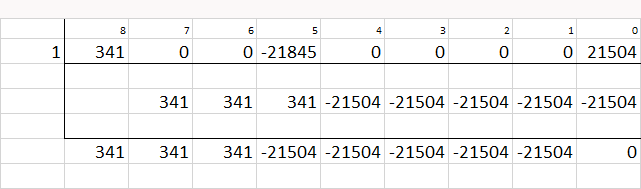
Which factorises to

This has real solutions r = 1 and r = 4

The solution r = 1 is discounted

so