Proof

Mathematics is largely based on logic – a structure
of rules used for reasoning.

Most of maths is written as statements :
words or symbols which contain information.

A statement may be true or false, and is made from
axioms, assumptions and arguments.

An axiom is a statement which is assumed to be true, and
is used to then develop a system. 
All logical systems must state its axioms.

An assumption, or premise,  is a statement, which may
 in reality be true or false but is taken to be true for the
argument which follows.

 

An argument is a set of statements which use logic
to  show how one particular statement occurs.

A proposition is a statement whose truth is to be shown by
the use of an argument.

A conjecture is a proposition which appears to be true, but has not yet been proved.

A theorem is a  statement which has been proved to be true.

A lemma is  a theorem which is used in the proof of another theorem.

A lemming is a small rodent which jumps of cliffs.

The converse of  a theorem or statement  takes the conclusion as the starting point, and the starting point as the conclusion.

The inverse of a statement changes its polarity.

The contrapositive of a statement is the negation of the converse.

The negation of a statement is made by putting a NOT in it!

Example

If it rains today, we shall have cake tomorrow.
inverse: If it does not rain today, we shall not have cake tomorrow.
converse: we shall have cake tomorrow if it rains today.
contrapositive :we shall not have cake tomorrow if it does not rain today.

 

A proof is  a sequence of statements which lead to
 the establishment of the truth of one final statement.

A proof may be valid or invalid, depending on whether or not
the arguments used are correct.
One counter-example will show a statement to be invalid,
which will make the proof invalid.

Proof has its own notation:-

 

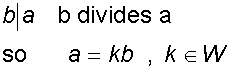
Direct Proof

This is proof in which all the assumptions used are true, and all the arguments are valid.

A series of linked implications lead from a given statement to a declared goal. The original statement is given to be true, implying the declared goal is also true.

Example

Given x is an even number, prove x² is an even number.

   

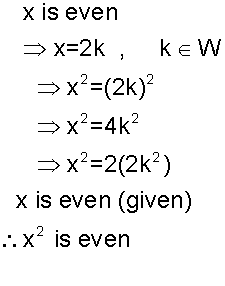
Example

Prove that the arithmetic series with first term a
and common difference d can be summed as shown:-

 

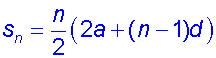
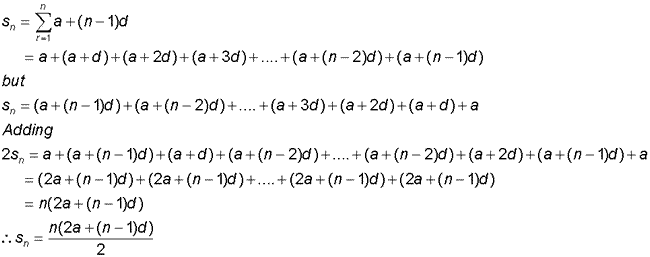
Indirect Proof (aka Proof by contradiction)

One assumption is made which is the negation of the statement to be proved.
Valid arguments are then used to arrive at a statement which is clearly false.
This contradiction then makes the original assumption false, thus making the statement to be proved true.

Example

Show by contradiction that the square root of any prime number is irrational.

    

 

Proof by Contrapositive

 Similar to above, however this time the contrapositive is used:- instead of a contradiction, the aim is to prove that if statement A implies statement B, then NOT B implies NOT A.

Example

Prove that if x = 89 then x is not divisible by 3.

 

Proof by Induction

1. A conjecture is made and shown to be true for numbers n and n+1.
2. Then it is shown to be true for a specific low number.
3. This then leads to the conclusion that it will be true for all values of n ≥ the specific value proved in step 2.

Note: The order of these steps does not matter

Example

 

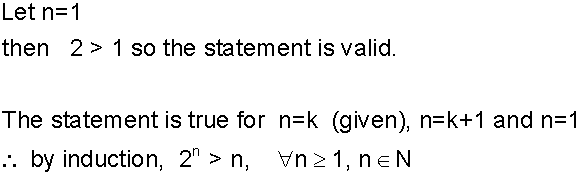
Example

 

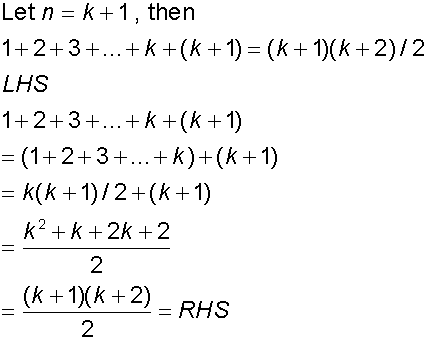
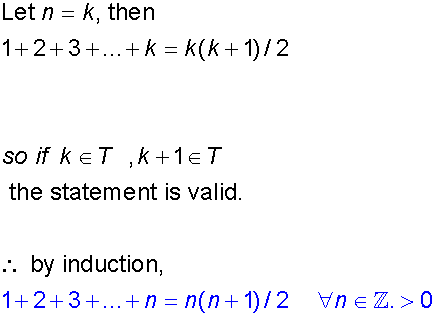
Example

Example

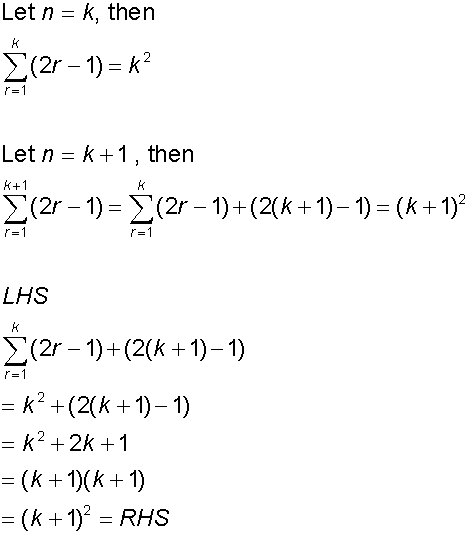
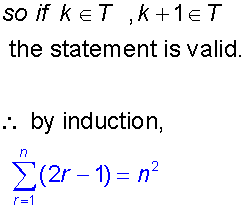
Example

 

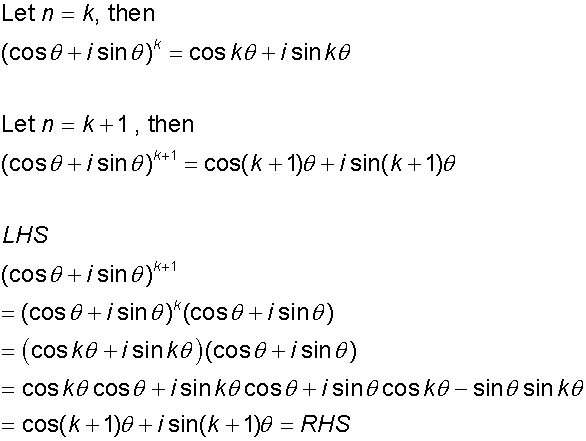
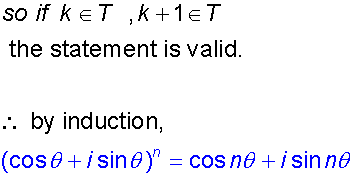
Example

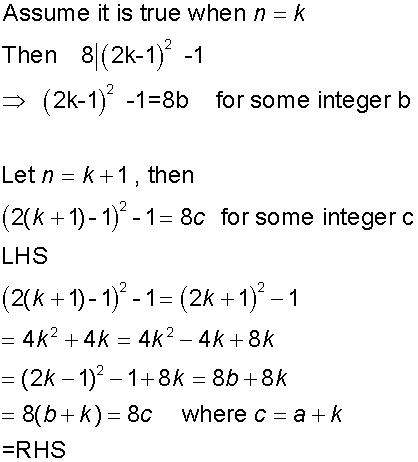
Example

 

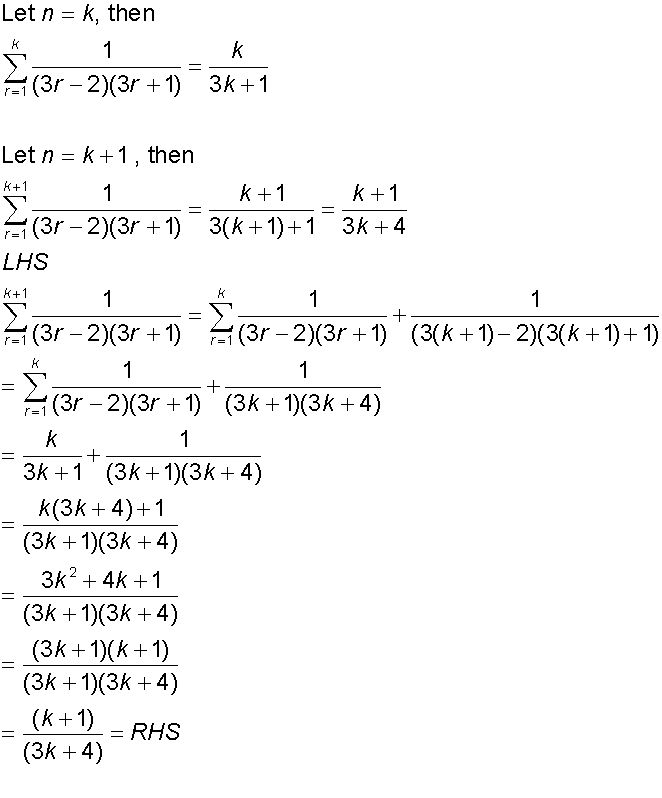
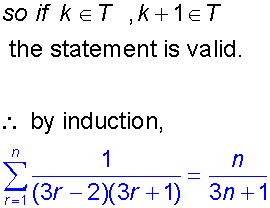
  Proof by Exhaustion

Here,  a proof is made by showing that the statement holds for every single possible case.