Completing the Square

Completing the square often aids in solving quadratic equations, and can be used to draw the graph of  quadratics.

To complete the square, a quadratic is written in a form which has a square term and a constant.

Example

 

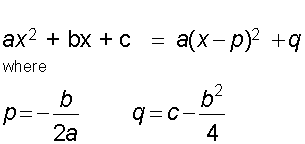
Perfect squares

If there is no constant term, then the quadratic is said to be a perfect square.

 

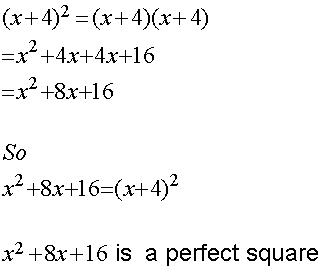
the following are shown in completed square form:

 

 

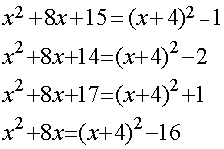
Co-efficient method

 

This method compares the coefficients of the original quadratic to those of the multiplied out completed form.

Examples

                                                          

 

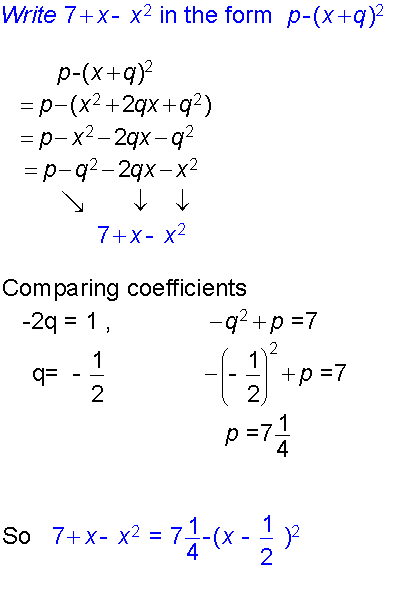
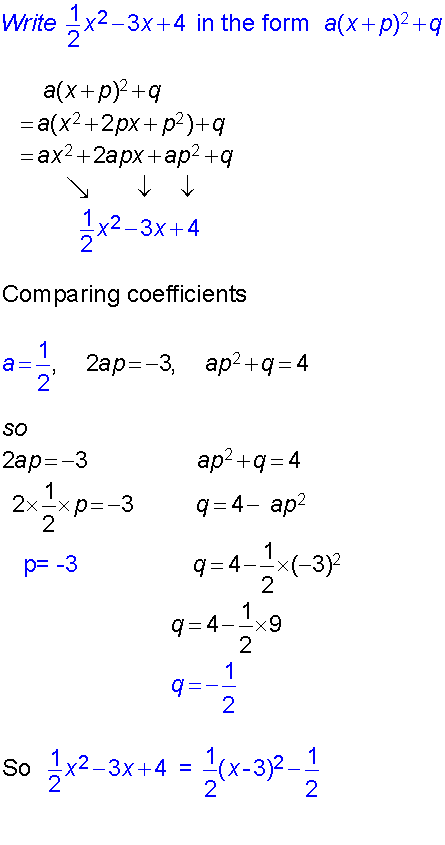
General method

Unitary x² coefficient

 

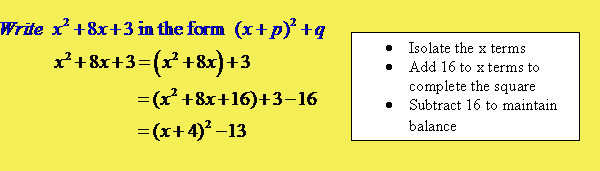
The following also works for x² + bx +c :-

• Write out the x inside a bracket.
• Put in half of b.
• Put a squared sign on the bracket.
• Subtract the square of the new end number.
• Add or subtract c

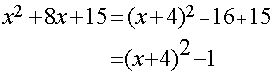
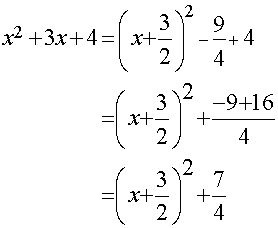
Non - Unitary x² coefficient

 

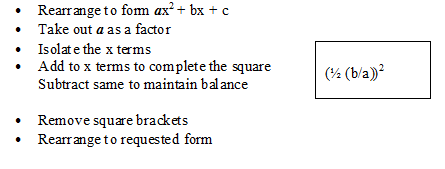
Examples

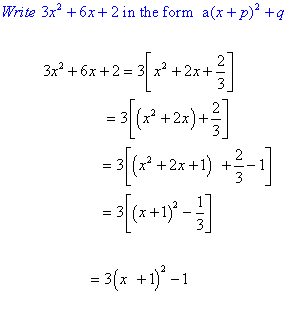
Skipping steps,

 

 

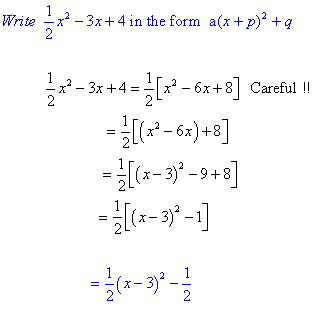
Turning point

 

 

 

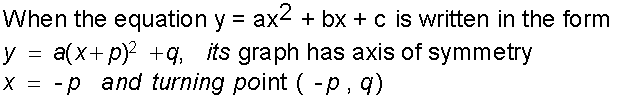
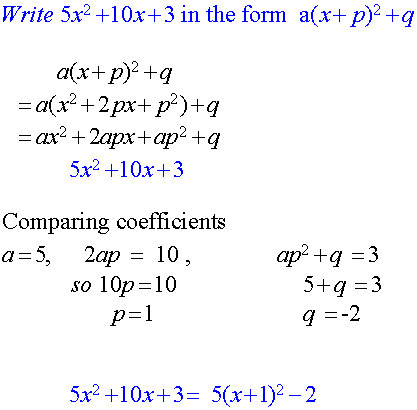
The turning point is (-1,-2)

 

Solving quadratic equations

Find the roots of the equation

Roots occur when

 

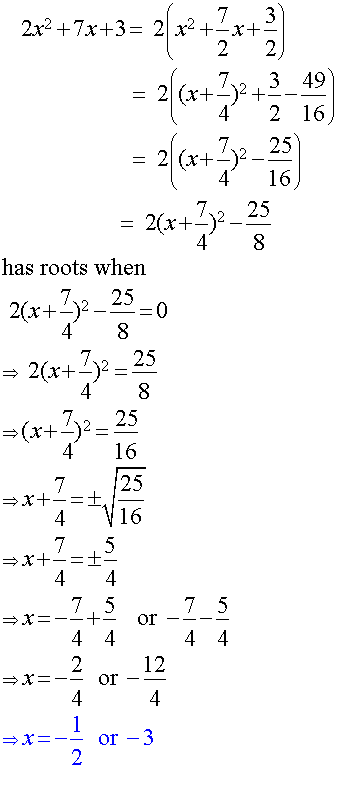
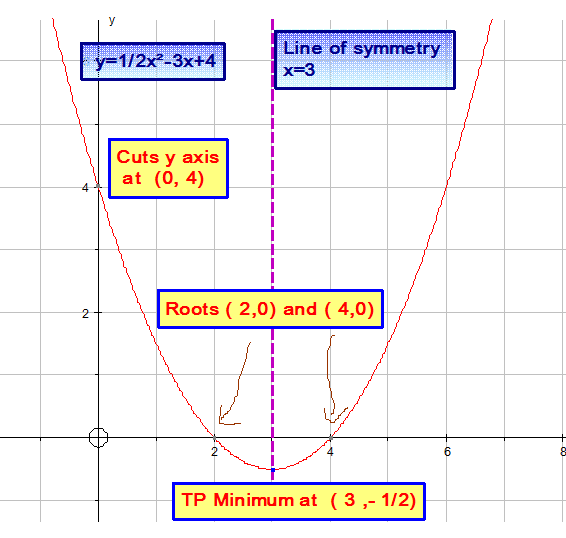
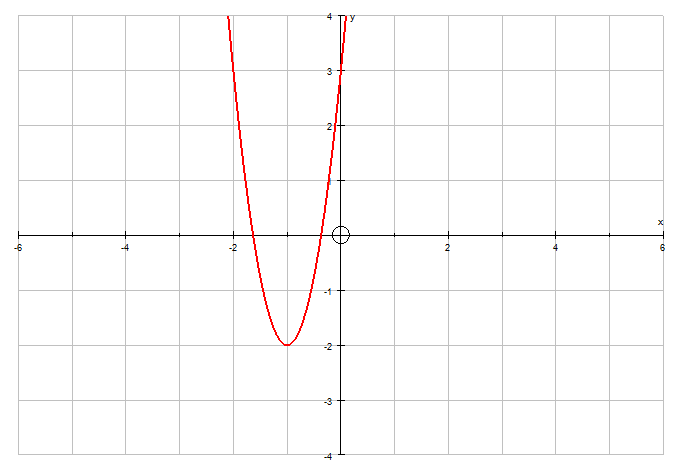
Graph Sketching from the completed square form

Earlier, it was shown that the quadratic

Can be written in completed square form as

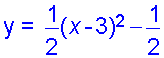
This immediately shows

1. The shape of the graph
   Here, it is U shaped, since it has a positive gradient. It will also be shallow, since the gradient is less than 1.
2. The turning point
   Here, the turning point is (3 , -1/2)
3. The axis of symmetry is the line x = 3
4. The minimum value is  y = -1/2
5. And, with a little extra work, The roots

(These occur when y = 0)

Here,

 

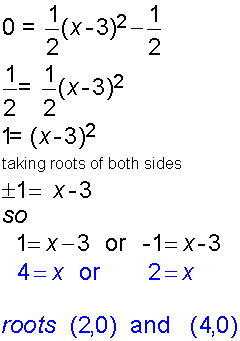
The y-intercept

 This occurs when x = 0
Here,

 

 

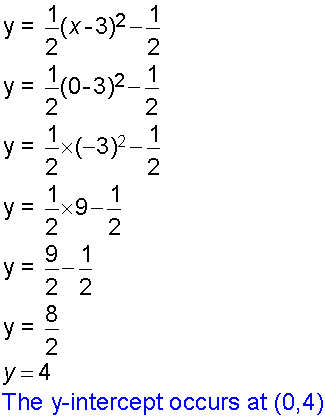
Putting these altogether:-