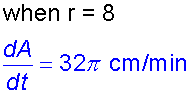Parametric Equations

Functions are often referred to in terms of two variables which can be plotted as one equation. For example, the function f(x) can be drawn as the graph y = f(x).

Sometimes, it is projectile motion , the object will be accelerated vertically due to the force of gravity, but continue to travel horizontally at a constant velocity.

The horizontal and vertical positions can be independently calculated at any given time t. If f(t) and g(t) are functions of t, then x = f(t) and y = g(t) define a point on a curve for each value of t.

x = f(t) and y = g(t) are called parametric equations, whilst t is the parameter.

 

Example

The path of an object defined by

x = 3( 1 + t )
y = 6( 1 − t )

has individual positions at t seconds :-

t	x	y
-5	-12	36
-4	-9	30
-3	-6	24
-2	-3	18
-1	0	12
0	3	6
1	6	0
2	9	-6
3	12	-12
4	15	-18
5	18	-24
6	21	-30
7	24	-36
8	27	-42
9	30	-48
10	33	-54

so when timing started, t = 0 and the object has co -ordinates (3, 6)

i.e. it is displaced 3 units horizontally from the origin and 6 units vertically.

Plotting the data  :-

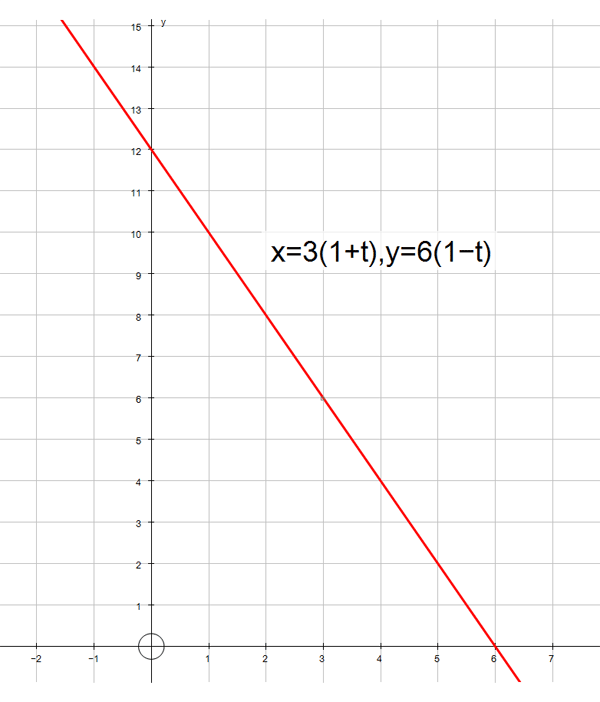
Which is a straight line.

But how can the two parametric equations be written as one equation in terms of y and x ?

Rearrange one of the equations .

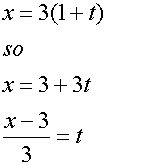
now substitute into the other

 

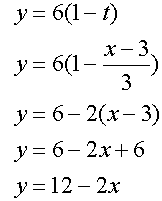
which gives y = 12 - 2x.

This is known as the constraint equation.

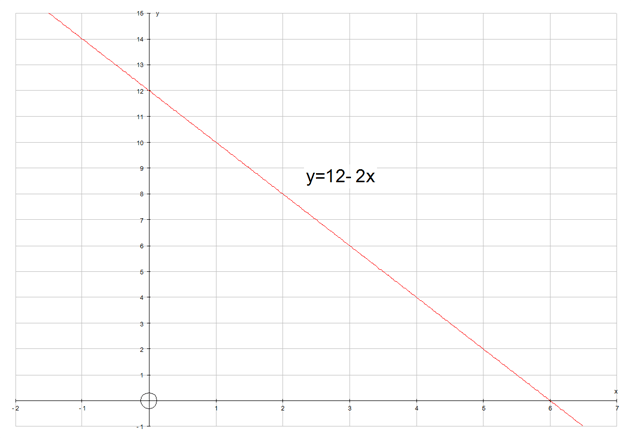
Constraint equations

how to try to get back to y = f(x)

 

Given x=f(t), t=f^-1(x)
so  y=g(t) becomes y=g(f^-1(x))

Example

Find the constraint equation
of the parametric equations
x = 4 - t
y = 1 + 3t

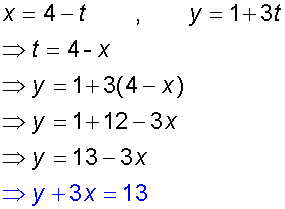
This is a straight line .

 

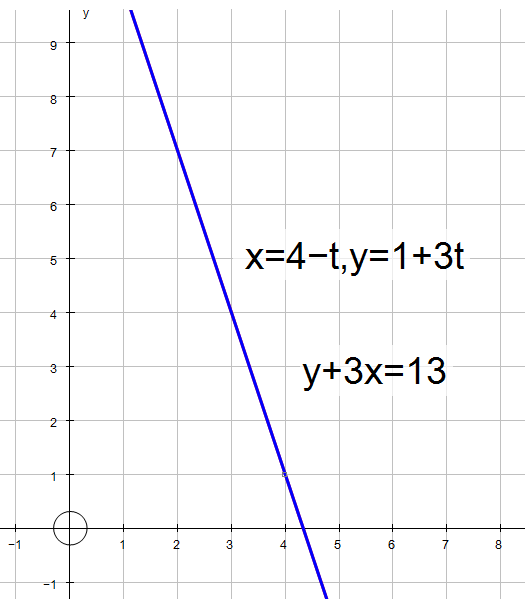
Example

Find the constraint equation of the locus defined by
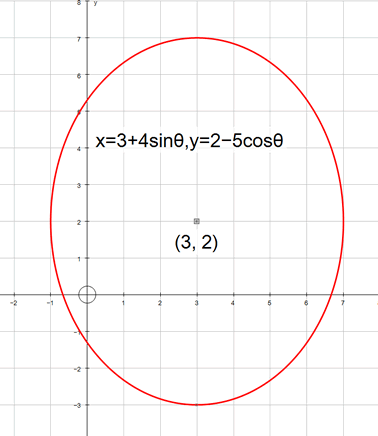
x = 3 + 4sinθ
y = 2 - 5cosθ

 

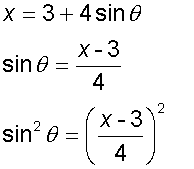
and

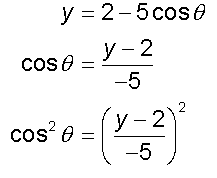
so

 

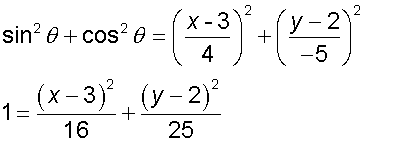
Which is the equation of an ellipse,
major axis parallel to the x axis, centre (3,2)
major axis length 8, minor axis length 10

 

 

The circle

     x = rcost
     y= rsint
    r is the radius of the circle with centre (0,0)

 

Example

     x = 3cost
     y = 3sint

represents a circle of radius 3, centre (0,0)

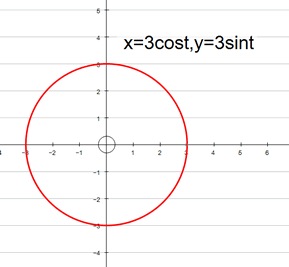
Where as
     x = 3 + 3cost
     y = 5 + 3sint

represents a circle of radius 3, centre (3,5)

 

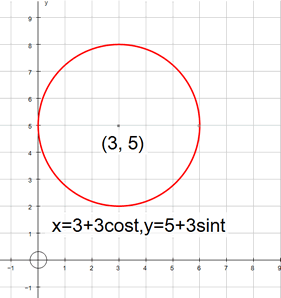
Differentiating parametric equations

First derivative

When x = f(t) and y = g(t) and y = f(x)

then
                

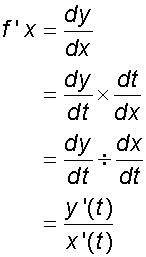
so

             

 

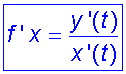
Example

Find an expression for the gradient of the
 curve defined by  x = t² ,  y = 4t

 

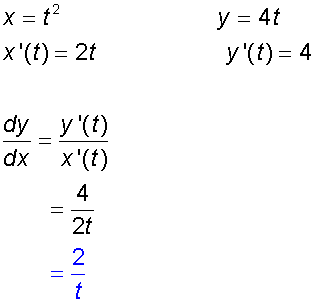
*Note*

The constraint equation is

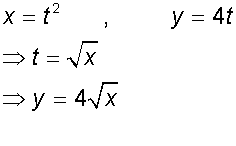
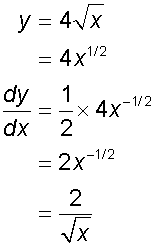
which is the same

 

Example

Find the equation of the normal at t = 3 on the curve
x = t² , y = t³

 

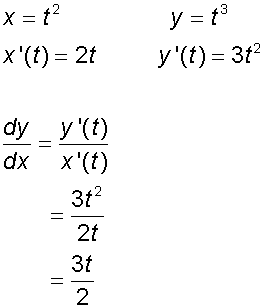
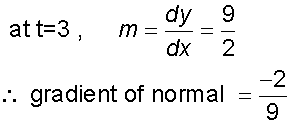
substitute into y-b=m(x-a)

 

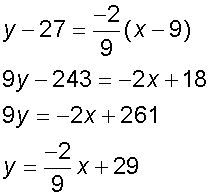
Second derivative

           

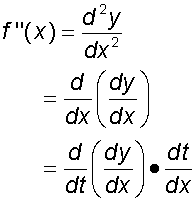
Substituting the equation for dy/dx

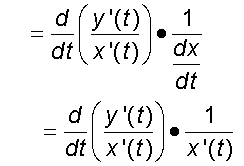
now apply the quotient rule

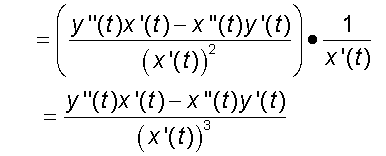
so

 

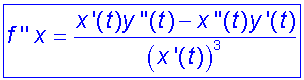
Example

Describe the nature of the curve
x = t² , y = t³ at the point t = 3.

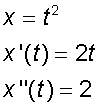
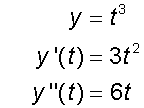
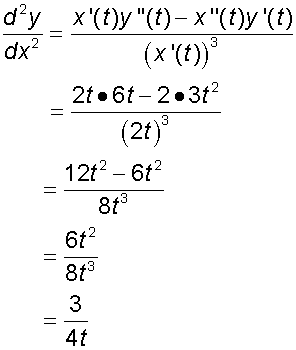
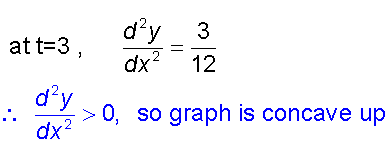
Example

Find the critical points of the following curve :-

 

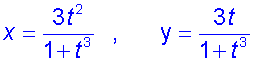
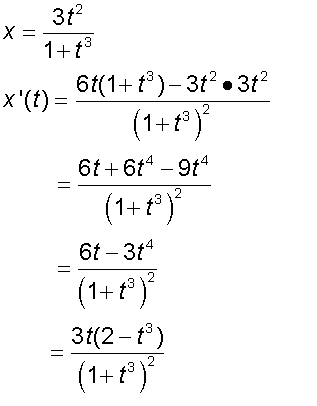
and

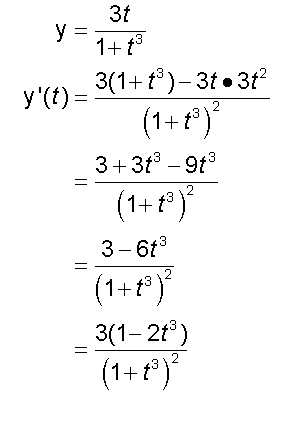
so

 

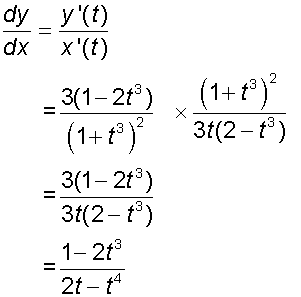
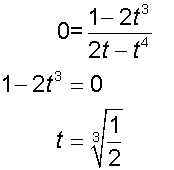so

 

 

 Other Uses

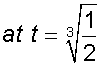
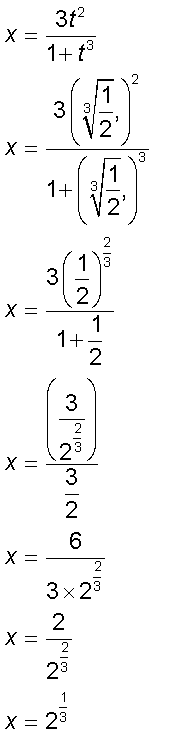
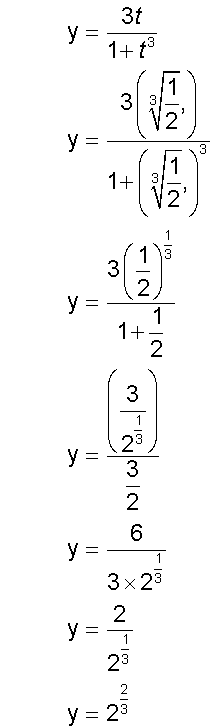
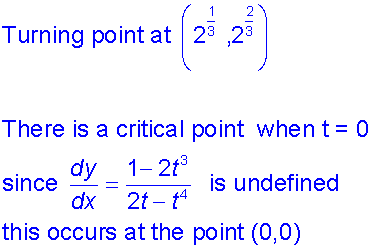
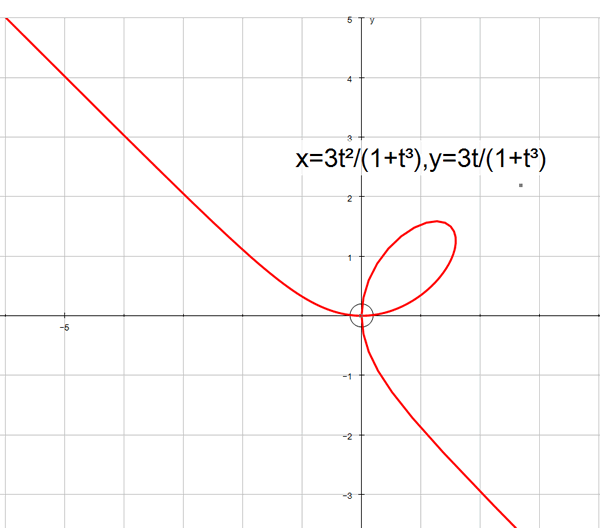
Projectile Motion Example

A projectile is fired horizontally at a speed of 250 m/s from the edge of a cliff which is 45 m high.

How long after firing does the projectile hit the ground ?

How far does the projectile travel horizontally ?

What is the horizontal and vertical velocity of the projectile when it hits the ground ?

What is the horizontal and vertical acceleration of the projectile when it hits the ground ?

 

Solutions

Newton's Equation of motion

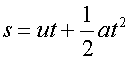
allows the vertical and horizontal displacement to be calculated separately.

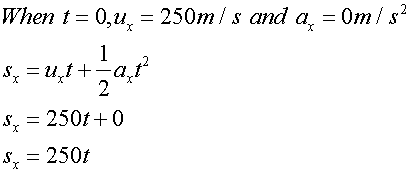
and

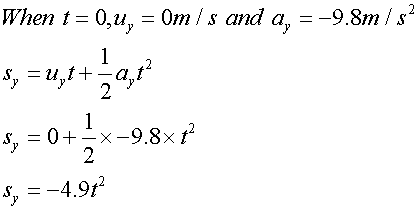
The original displacement is zero units in the x direction, but 45 units in the y direction, since the cliff is 45 m tall.

so

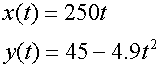
The individual positions at t seconds can now be calculated:-

t	x	y
0	0	45
1	250	40.1
2	500	25.4
3	750	0.9
4	1000	-33.4
5	1250	-77.5

From the table, the projectile hits the ground somewhere between 3 and 4 seconds after being fired.

Plotting these points give a picture of the flight path:

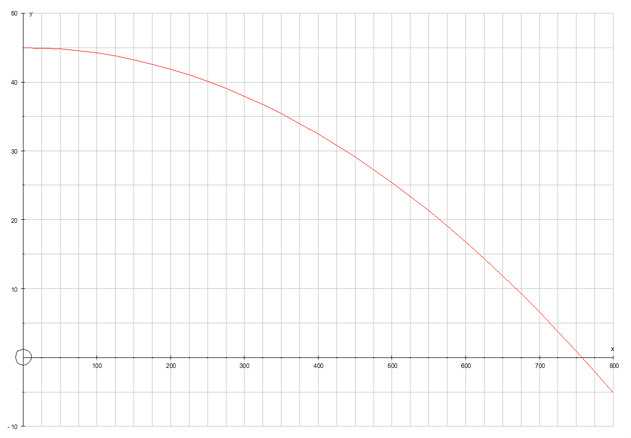
But when exactly does it hit the ground ?

The projectile hits the ground when y = 0

so

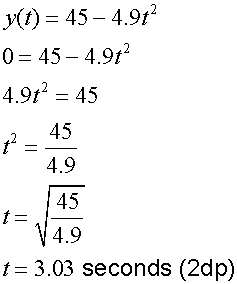
The projectile hits the ground 3.03 seconds (2dp) after being fired.

Substituting this value of t into the parametric equation for x :-

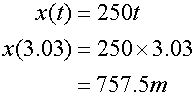
so the projectile has travelled 757.5 m horizontally.

 

The constraint equation is

 

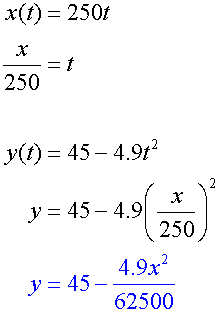
this can be used to check the horizontal distance travelled, since y = 0 at ground level

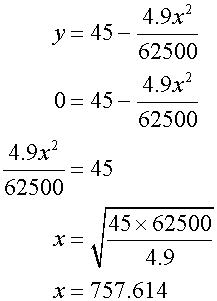
Why is there a difference ? Because the time was rounded.

Finding the horizontal velocity

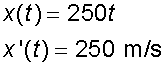
(which is , of course, as stated in the question!)

and the vertical velocity

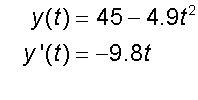
so when the projectile hits the ground, it has a vertical velocity

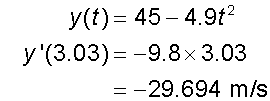
The negative value shows that it is travelling downwards.

What about acceleration ?

This is the second derivative.

Horizontally,

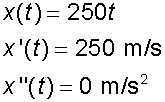
(as expected since travelling at a constant velovity)

and vertically,

 

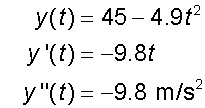
which is acceleration due to gravity.

 

 

 

Example

 

The radius , r cm, of a circular  pool of water is
 increasing at a  constant rate of 2cm per  minute.
Find the rate at which the area of the pool is increasing
with time, when the radius is 8cm.

 

Start by writing down what you want and what you know

 

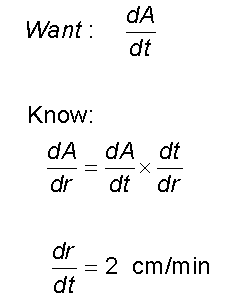
Work out equation

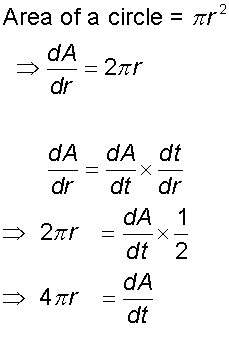
Substitute