The modulus function   y =│x│

The absolute value of x is defined as

This always gives a positive result.

Example

      y=3x²+6x-2 has graph

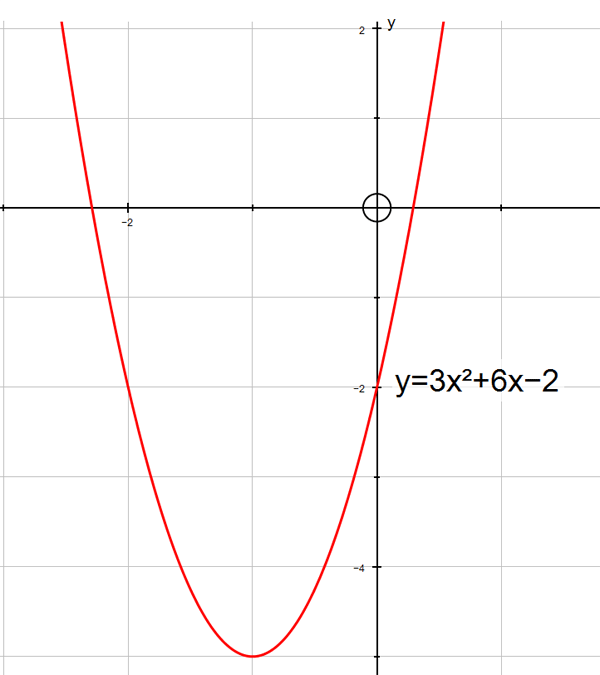
Whereas

y=|3x²+6x−2| has graph

 

Note how the negative portions have been
 reflected in the x-axis.

 

Examples

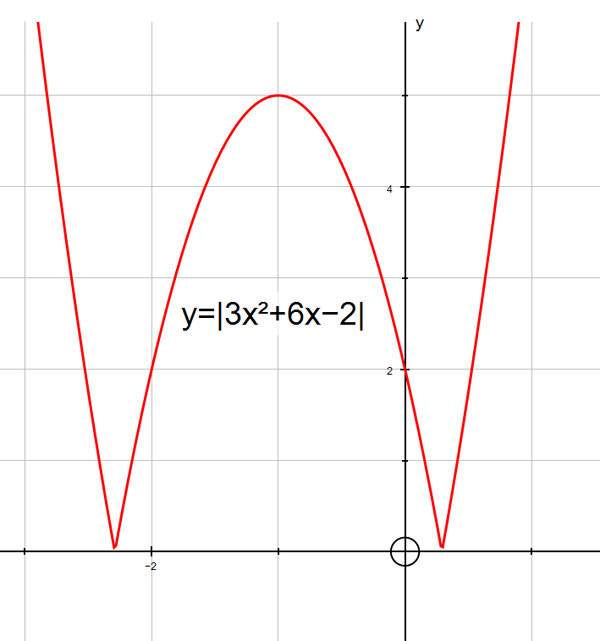
y =| 3tanx|

 

y =| 3x + 2|

 

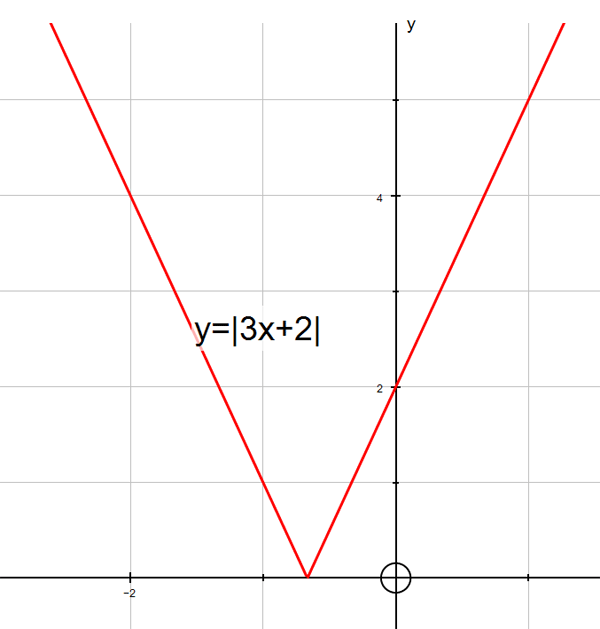
Odd and Even functions

Odd functions have half-turn symmetry about the origin,
so     f(-x) = - f(x)

Example

   y=x³ 

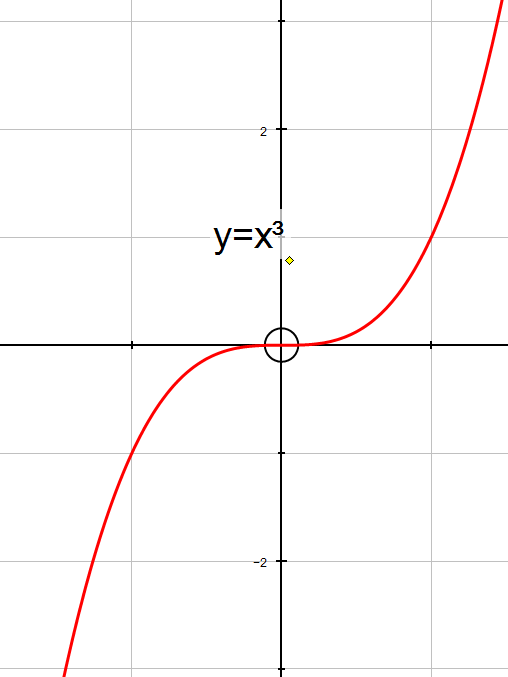
  y=x⁵−3x

 

 

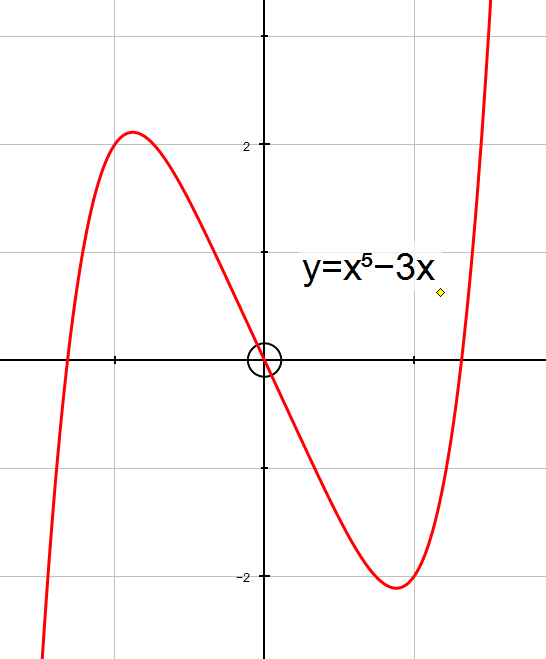
Example

Show that x⁵+ 3x³ is an odd function.

 

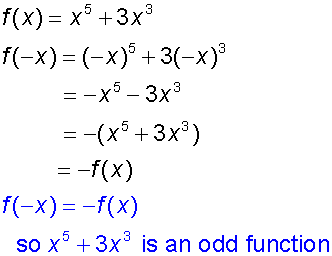
Even functions are symmetrical about the y – axis
so     f(-x) =  f(x)

Example

   y=x⁴ - 1

 

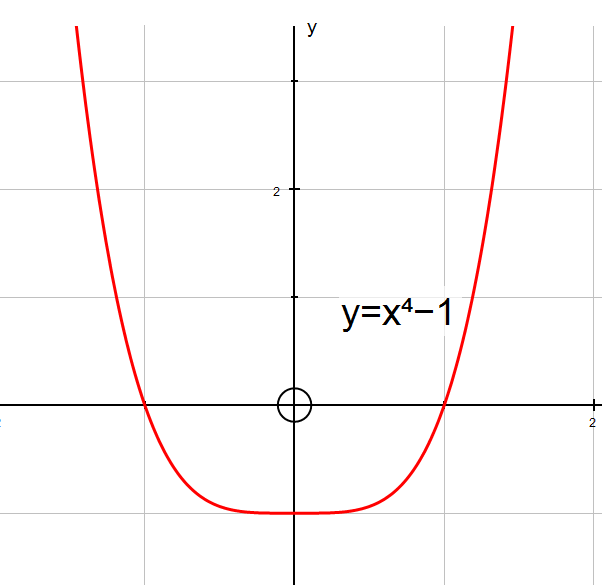
Example

Is  x⁶+ 3x²  an even function ?

 

 

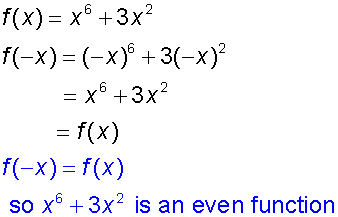
Asymptotes

Symbolab Asymptote Calculator

An asymptote to a curve is a straight line which
 the curve approaches but never reaches.

Example

f(x) = 1/x
 

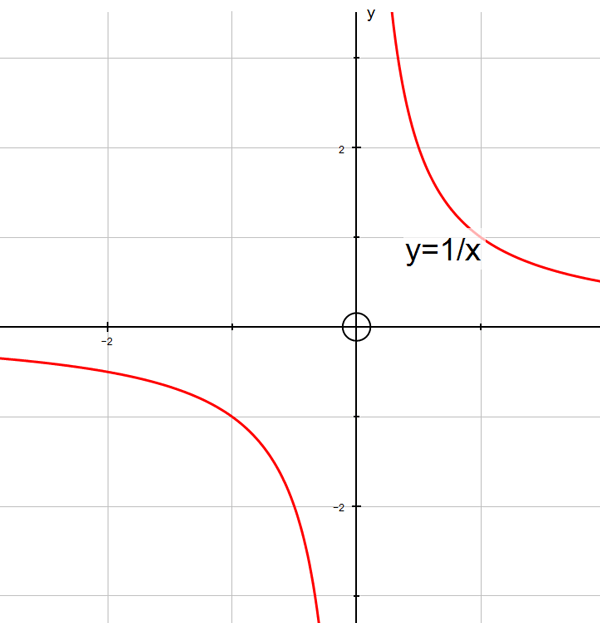
The graph y=1/x has vertical asymptote x=0
and horizontal asymptote y = 0.

To the left of the line x=0, f(x) tends to  - ∞
as x tends to zero.

To the right of the line x=0, f(x) tends to  ∞
as x tends to zero.

Example

f(x) = (x-3) /(x³+1)

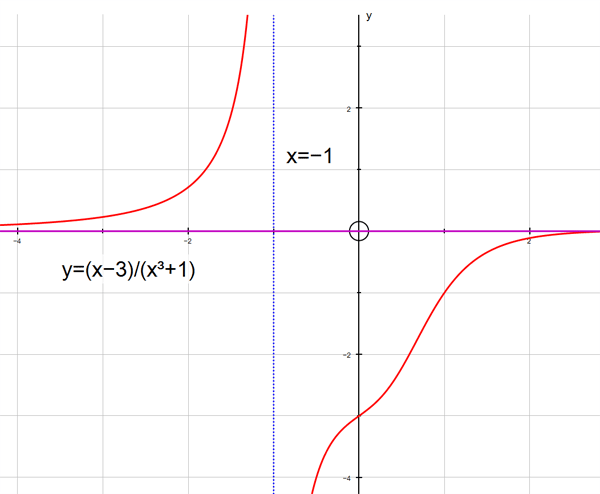
The graph y= (x-3) /(x³+1) has vertical asymptote x=-1
and horizontal asymptote y = 0.

To the left of the line x=-1, f(x) tends to ∞
as x tends to -1.

To the right of the line x=-1, f(x) tends to  -∞
as x tends to -1.

 

Example

f(x) = (x+1)(x−3)/(x+3)(x−4)

 

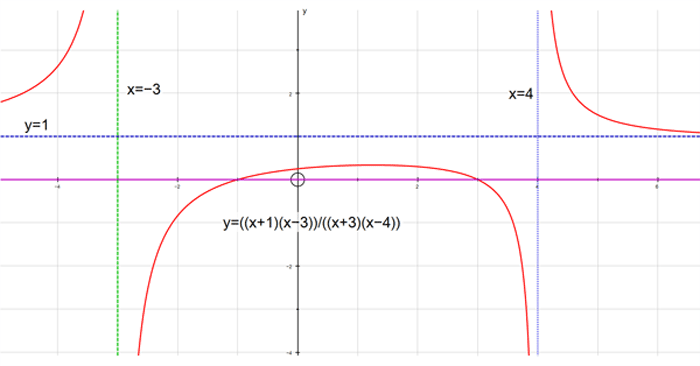
The graph  has vertical asymptotes x=-3 and x=4
and horizontal asymptote y = 1

 

Finding asymptotes

Vertical asymptotes are found by considering what makes the denominator zero.

Horizontal and oblique asymptotes need a little further action.

  

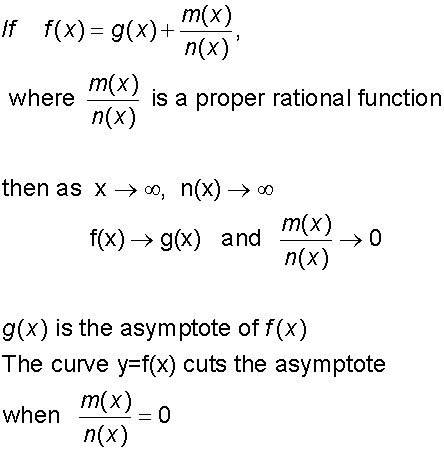
Use algebraic division to reduce the function.
The quotient becomes the asymptote.

Example

Find the asymptotes of the function

  

 

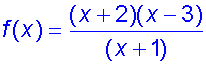
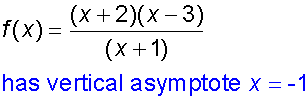
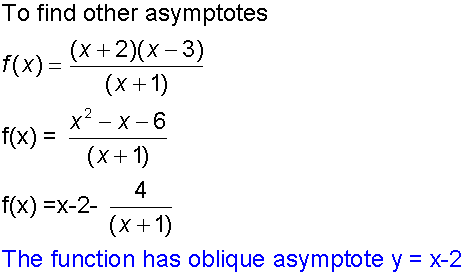
Alternatively:-

Asymptotes parallel to the x-axis can be found by equating the co-efficient of the highest power of x to zero. Those parallel to the y-axis can be  found by equating the co-efficient of the highest power
of y to zero.

 To find oblique asymptotes, substitute y=mx+c into the equation and equate the co-efficients of the two highest powers of x to zero.

Example

Sketching Asymptotes

To sketch a function which has asymptotes,follow these steps :-

• Identify any vertical asymptotes
• Identify any horizontal or oblique asymptotes
• Identify the y – intercept
• Identify the x – intercept
• Find stationary points
• Identify nature of stationary points
• Investigate what happens as values approach infinity
• Sketch and annotate

 

Example

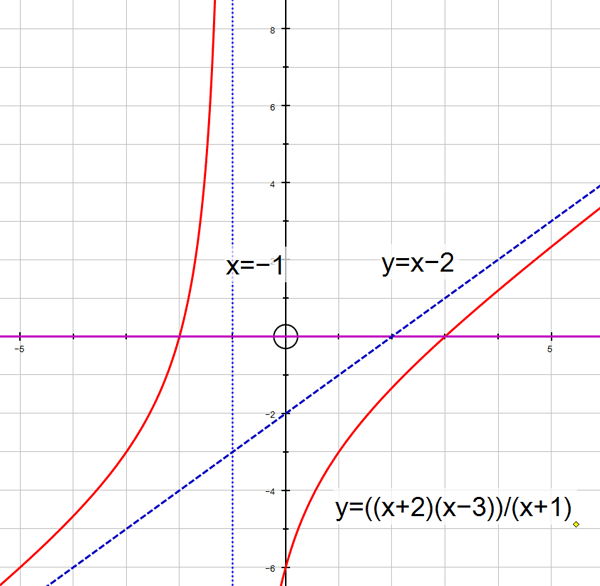
Using the example above, sketch the function

 

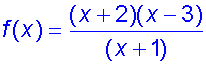
Vertical asymptotes are found by setting the denominator to zero:

 

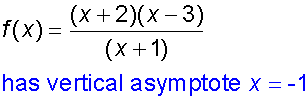
Horizontal and oblique asymptotes are found by dividing through the fraction:

 

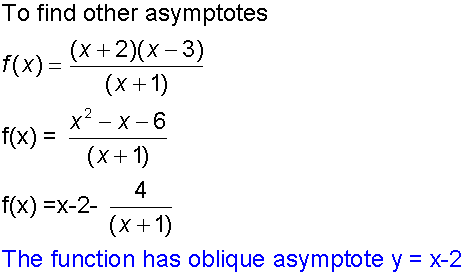
The y - intercept occurs when x = 0

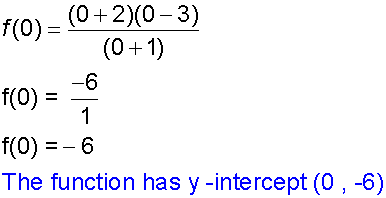
The x - intercept occurs when y = 0

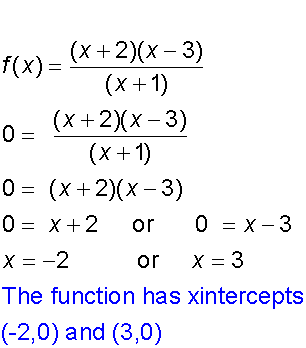
To find the stationary points,  set the first  derivative
 of the function to zero, then factorise and solve.

 

 

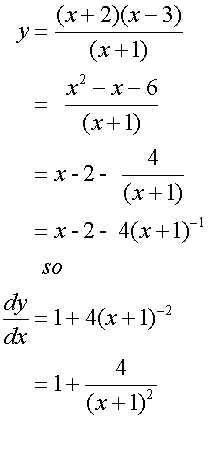
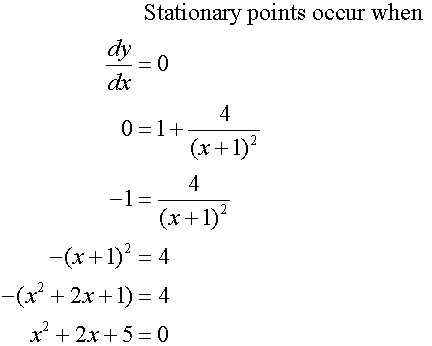
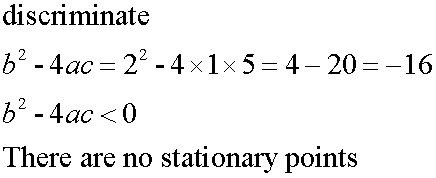
Sketch the graph

 

 

Example

sketch the function

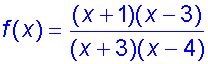
Vertical asymptotes:

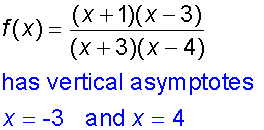
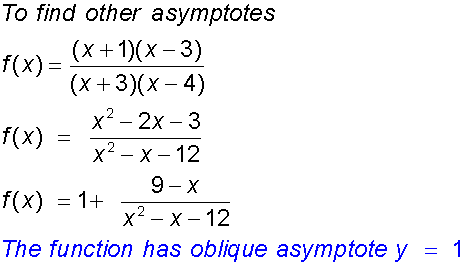
The y - intercept :

 

The x - intercept:

Stationary points :

 

 

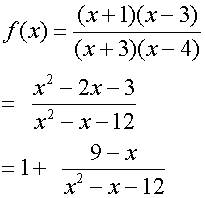
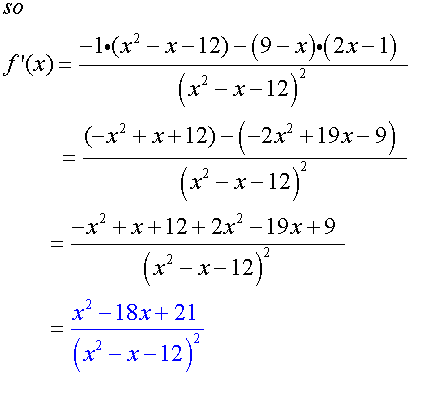
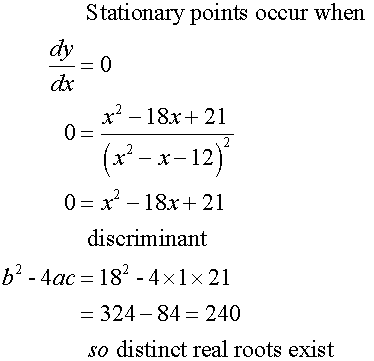
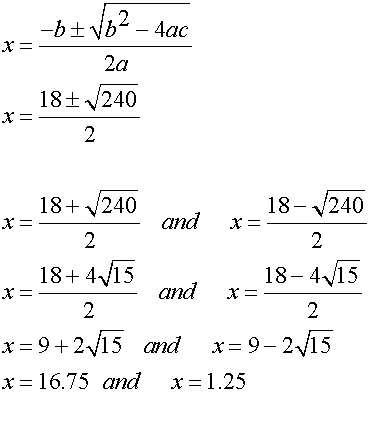
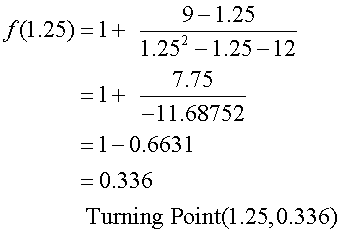
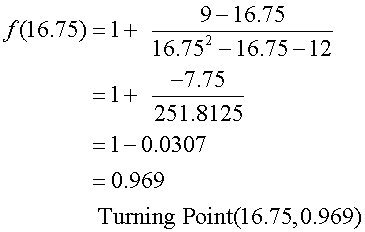
Find nature of turning points

 

 

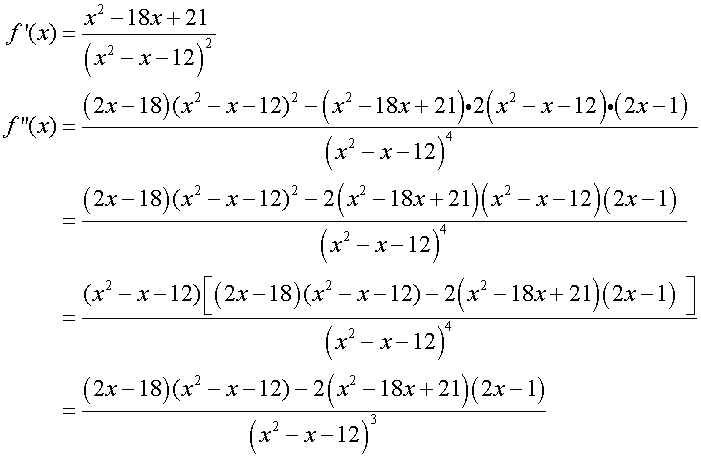
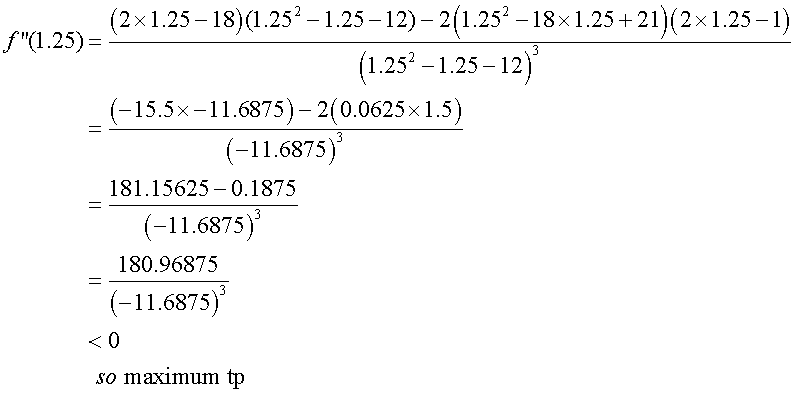
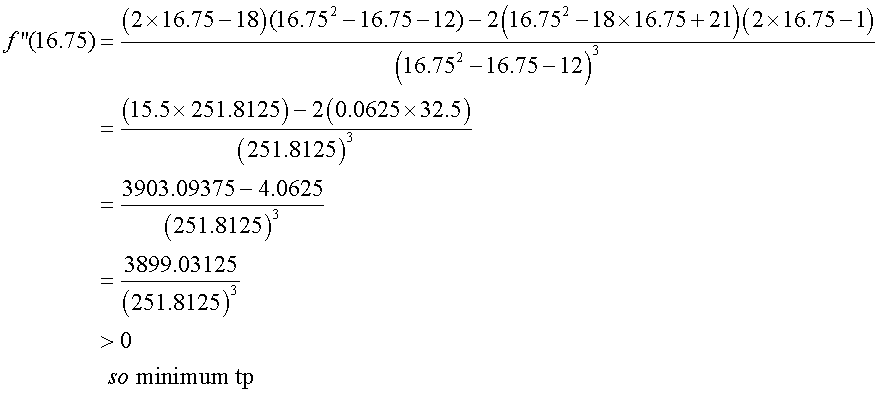
Sketch