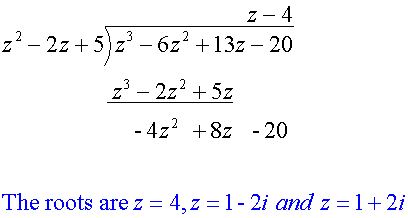Complex Numbers

Sets reminder

 

 

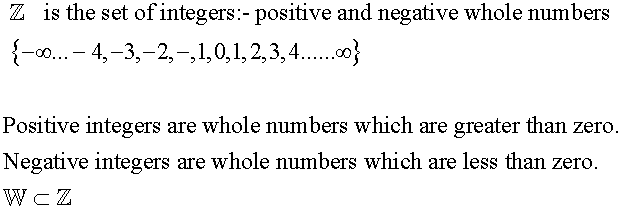
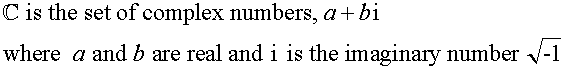
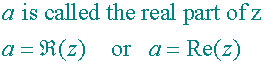
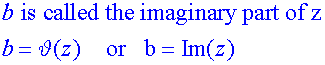
Complex conjugate

This is reflection in the real axis

 

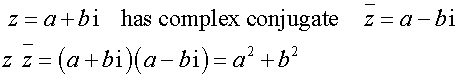
Example

 

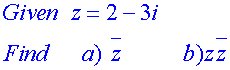
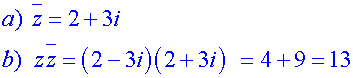
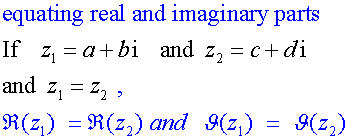
Arithmetic operations

 

 

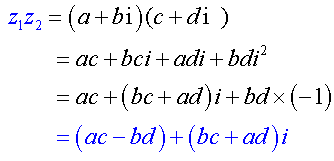
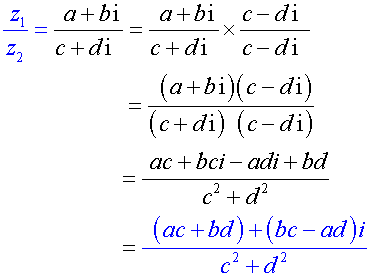
Example

Solve the equation x²- 2x + 5 = 0

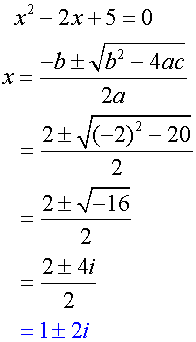
Example

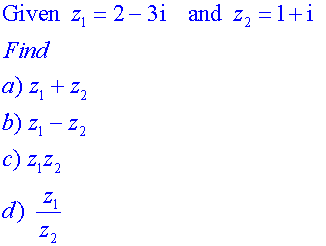
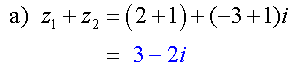
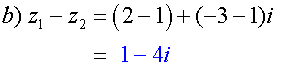
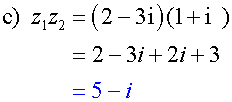
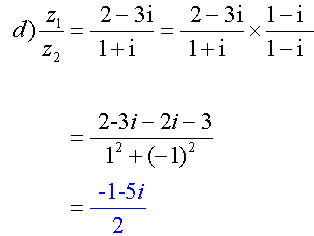
Alternatively,

  

 

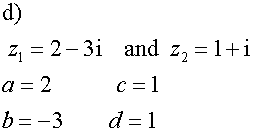
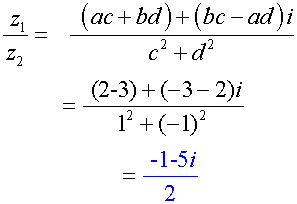
Inverse

 

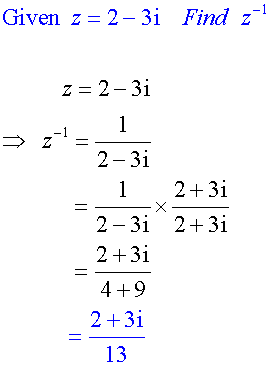
Argand diagrams

 

z = x + iy  can be represented on the complex plane
 by the point P(x,y)

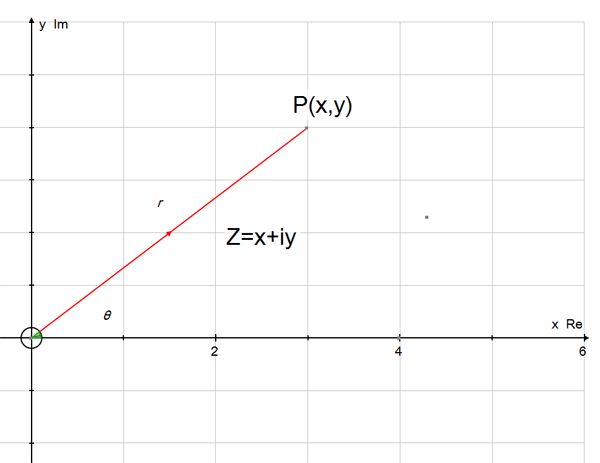
Points on the x axis are real.
Points on the y axis are imaginary.

z = x +iy  can also  be represented
by the vector 

 

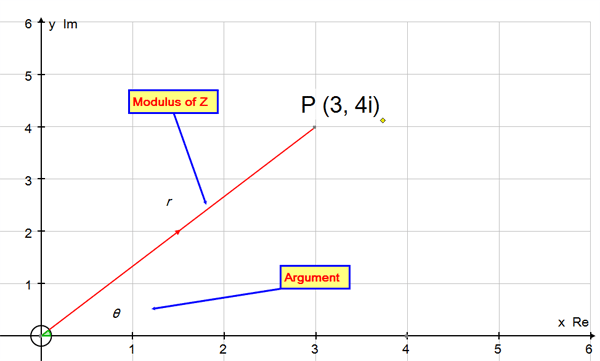
The length of    , r, is called the modulus of z.

By Pythagoras’ Theorem

 

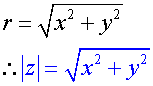
The size of the rotation is called the amplitude or
argument of z.

Arg z = θ + 2nπ

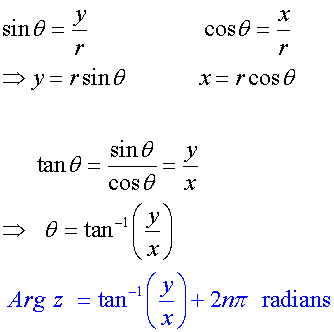
The principal argument is denoted arg z and lies
in the range  –π< θ ≤ π

 

Example

Find the modulus and argument of the complex
number z = 3 + 4i

 

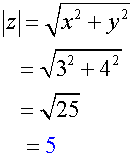
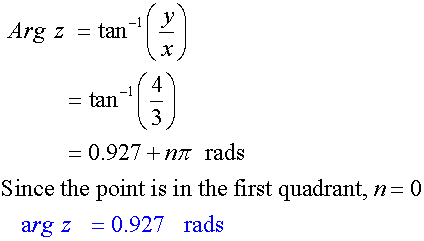
Loci

Given that z = x + iy, find the equation of the locus of the following :

 

 

 

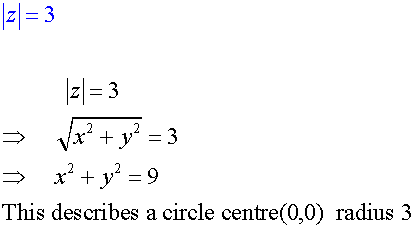
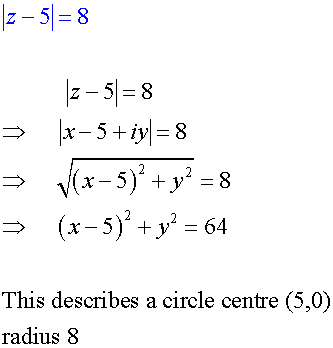
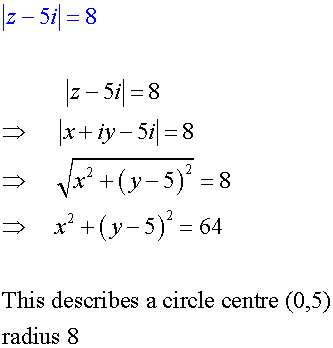
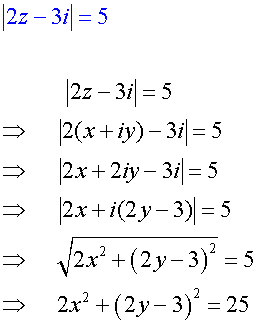
This describes an ellipse with centre (0,3/2)

 

 Polar form 

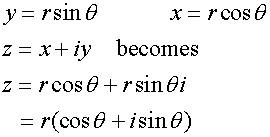
Example

Express z = 3 + 4i  in polar form

     

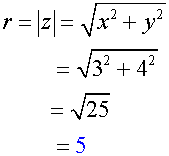
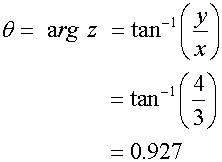
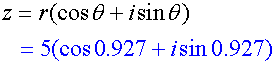
Note

 

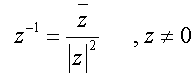
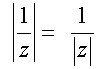
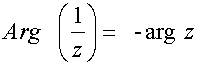
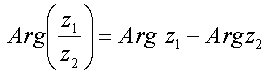
 De moivre's theorem

Example

 Given z = 3 + 4i  , calculate z⁵

     

 

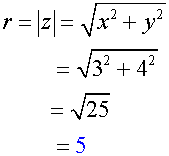
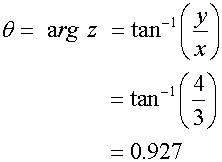
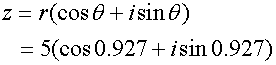
Roots of a complex number

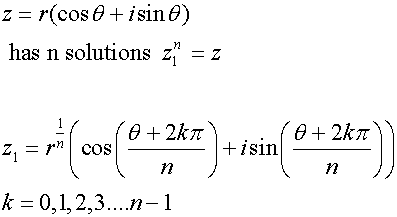
Example

Solve the equation  

     

 

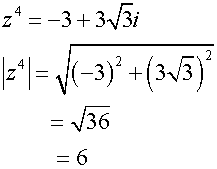
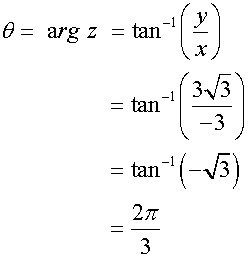
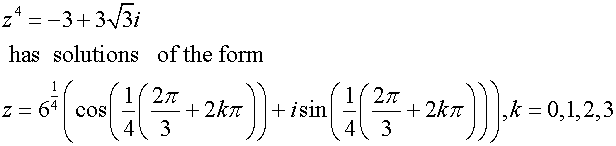
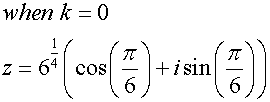
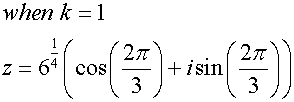
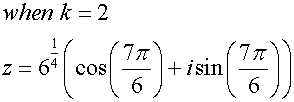
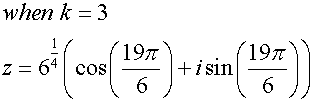
Complex roots

If the root of a polynomial is unreal,
it has complex roots

r(cosθ +isinθ)  and r(cosθ -isinθ) 

 

A polynomial of degree n will have n complex roots.

Example

Find the roots of the equation
 z³- 6z²+ 13z - 20 = 0 , given  z = 1 + 2i is a root

If z = 1 + 2i is a root , then so is its conjugate z = 1 - 2i

Factors are z -1 -2i  and z -1+2i