Definitions
Physical quantities usually fall into one of two categories:-
Scalar or Vector
Scalars
A scalar quantity is defined totally by its magnitude (its size) and units.
A few scalars (not exhaustive)
- Distance
- Speed
- Time
- Temperature
- Energy
- Work
- Power
- Mass
- Volume
- Area
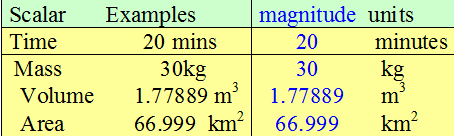
A speed of 60 mph is a scalar quantity.
Vectors
A vector quantity is defined totally by its magnitude, units and direction.
A few vectors (not exhaustive)
- Displacement
- Velocity
- Acceleration
- Force
- Weight
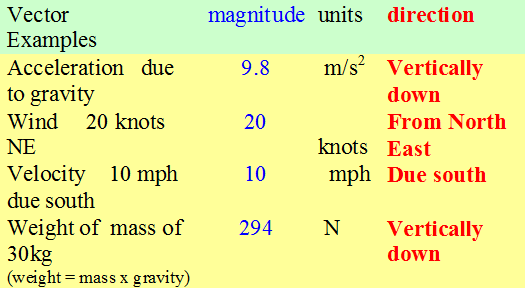
Speed is not a vector, since it doesn’t have a direction.
Velocity is a vector, so must have a direction.
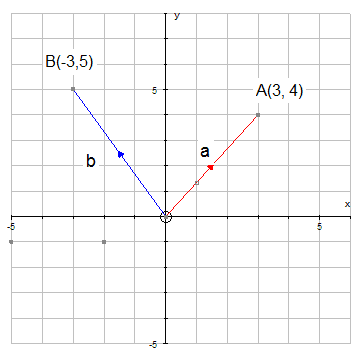
Writing vectors
A vector can be drawn as a line, with the length of the line representing the magnitude and the direction indicated by an arrowhead.
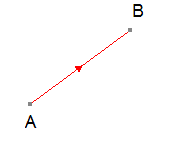
Vector AB is written as
![]()
The vectors below are shown in component form.
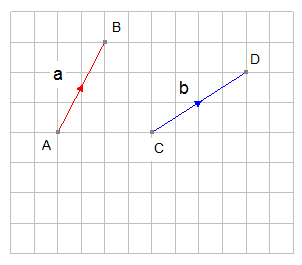
Vector AB is written as
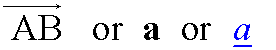
[Since you cannot write in your jotter in bold]
Notice that B is displaced 2 boxes to the right of A and 3 boxes up.
i.e. 2 units in the x direction and 3 units in the y direction.
The components are written as a vector column
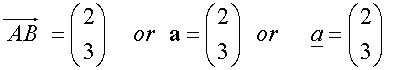
Likewise,
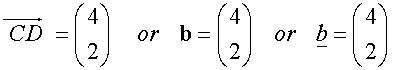
Column Vectors
When the co-ordinates of the end points are not known:-
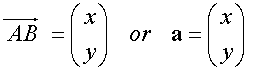
Or in 3-D
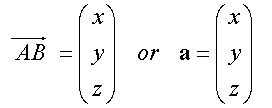
When the co-ordinates of the end points are known:-
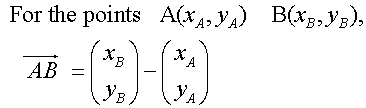
Or in 3-D
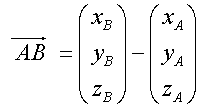
Examples
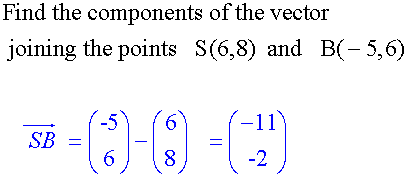
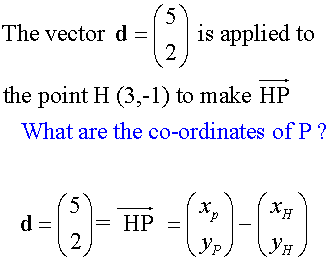
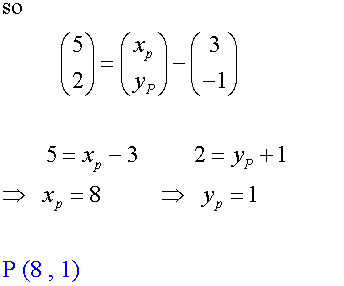
Equal Vectors
Each of these lines represent the vector
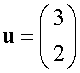
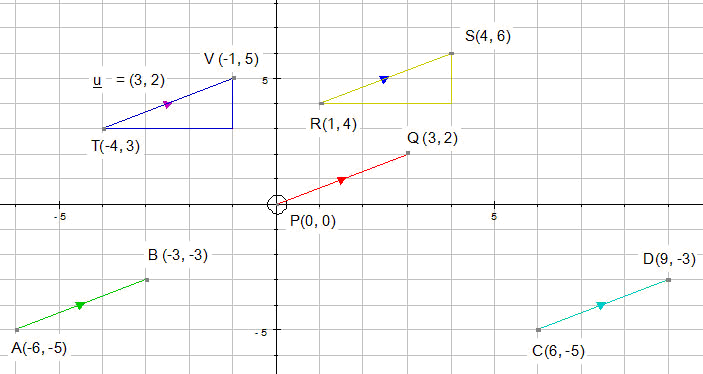
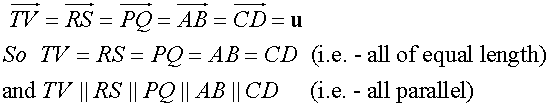
Direction is important
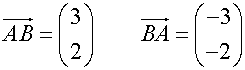
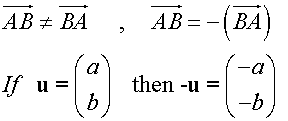
Magnitude
A vector is always the hypotenuse of the right angled triangle formed by its x, y and z components.
The magnitude of a vector is found by using Pythagoras’ Theorem.

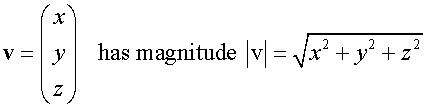
The magnitude is always a positive number !
Examples
Calculate the magnitude of each of the following vectors:-
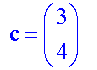
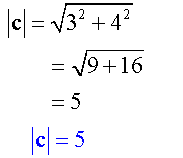
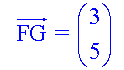
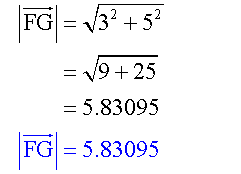
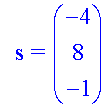
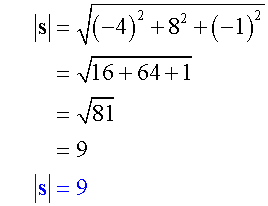
Example
Three points on a diagram have co-ordinates
P (3,4,-1) Q (9,8,11) and R (-9,-2,3)
Show that triangle PQR is isosceles
To be an isosceles triangle ,triangle PQR must have two sides of equal length.
Start by writing each column vector.
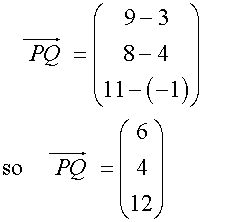
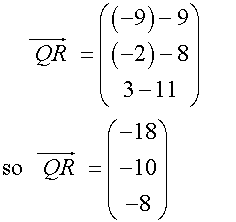
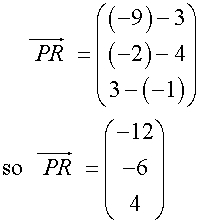
Find the magnitude of the vectors.
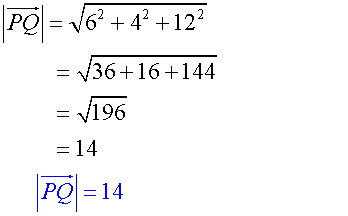
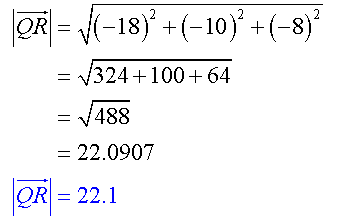
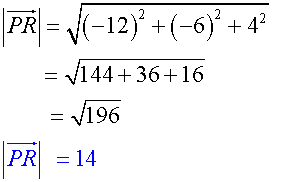
![]()
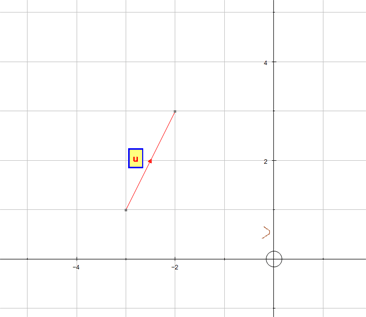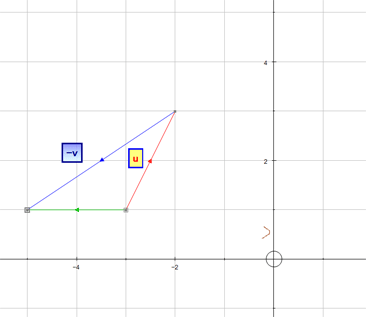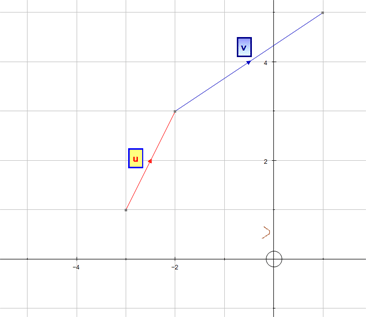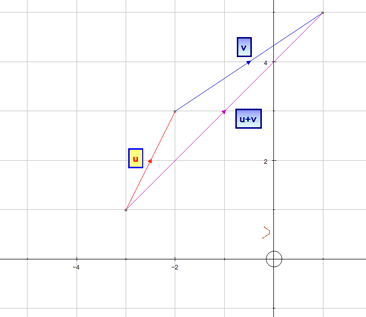
Adding Vectors
Vectors are added nose to tail,
to create an overall (resultant) vector.
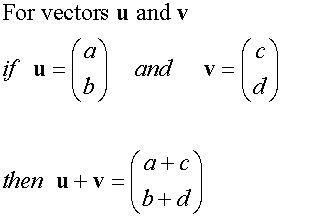
Example
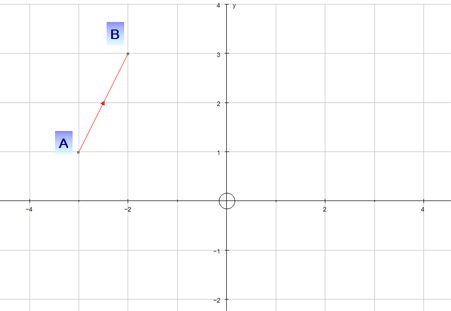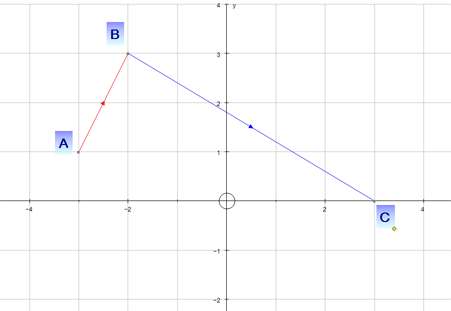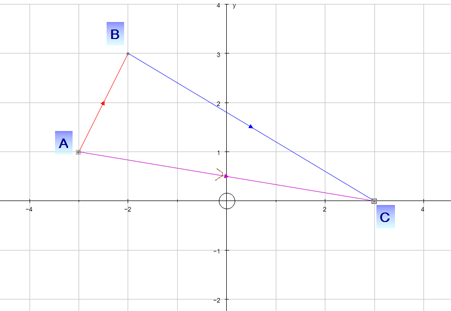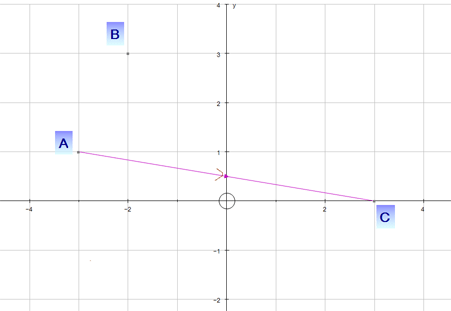
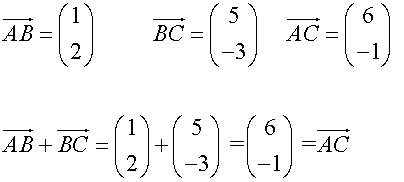
Example
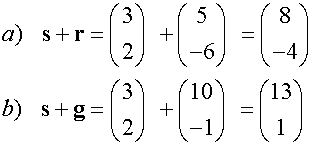
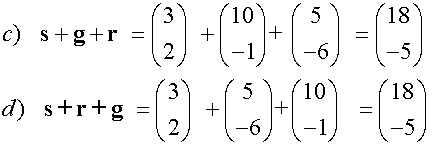
Subtraction of vectors
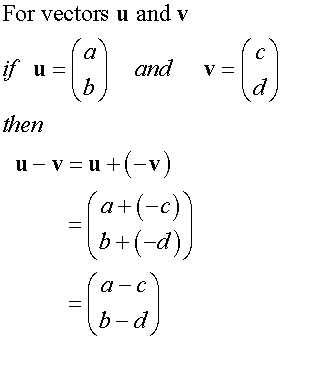
Example
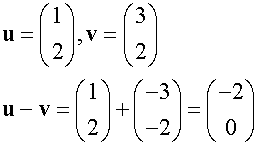
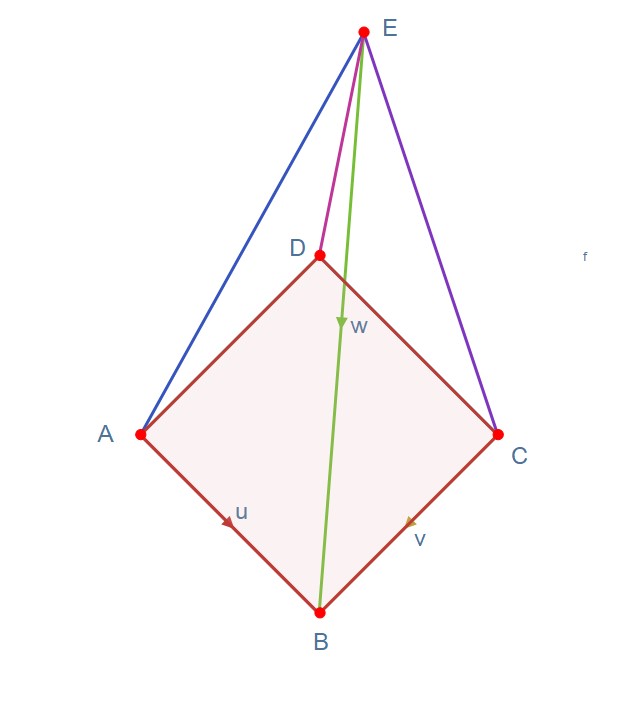
Vector paths
The shape below is a square based pyramid.
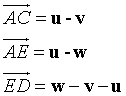
The Zero Vector
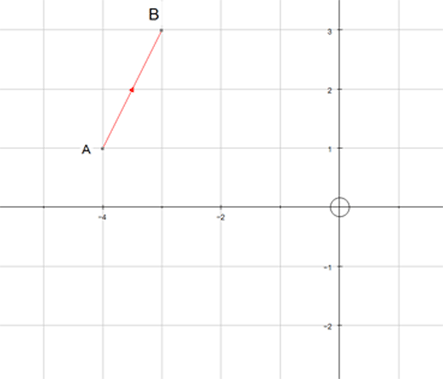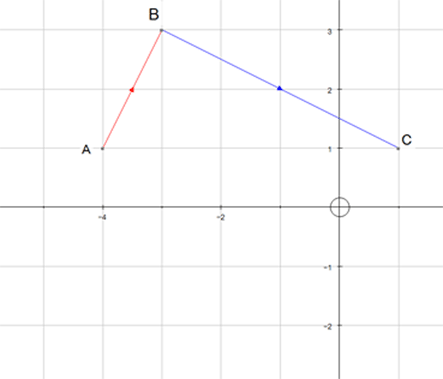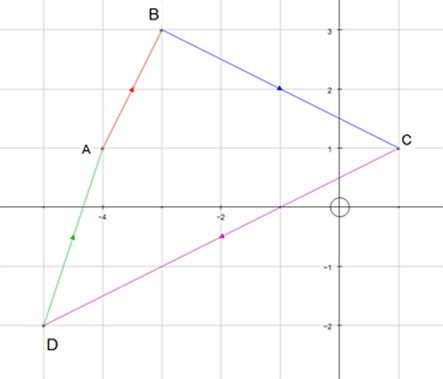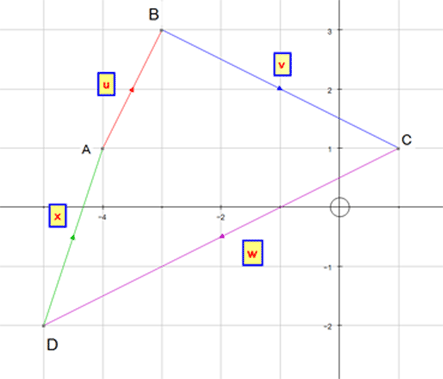
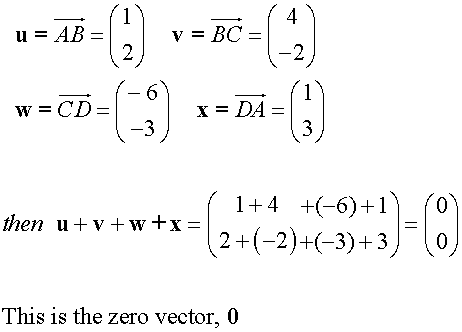
Note: Although travelling from A to B and back again has resulted in zero displacement from A,
the distance travelled is the sum of the magnitudes.
Unit Vector
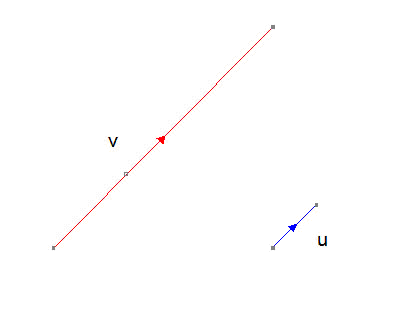
For any vector v, there is a parallel unit vector of magnitude 1 unit.
Example
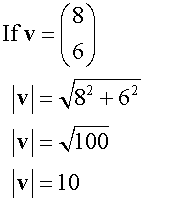
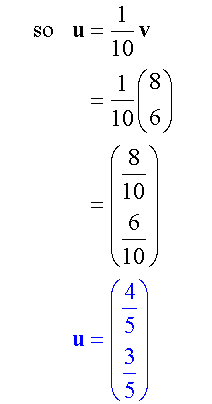
Position vector
A position vector is given relative to the Origin O.

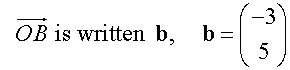
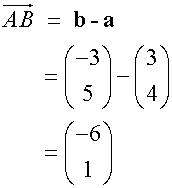

3 D Vectors
A vector may be described in terms of unit vectors i. j and k where
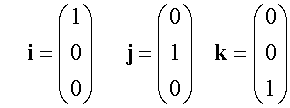
Example
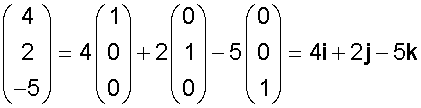
In General, the position vector of a point beginning at the origin and ending at point (x, y, z) is written
![]()
Multiplication of a vector by a Scalar
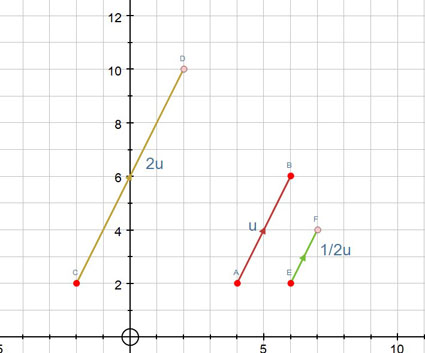
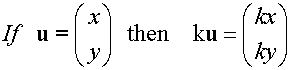
Example
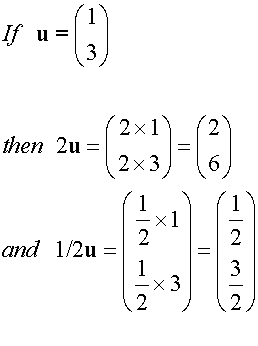
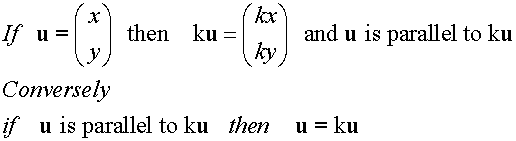
Collinearity

Example
Prove that the points A(1,1) , B(3,3 ) and C (4,4) are collinear and find the ratio in which B divides AC
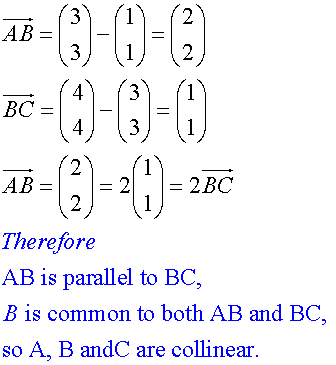
Ratio in which B divides AC
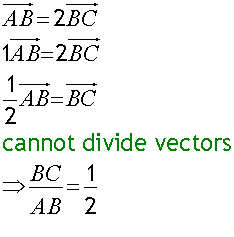
AB : BC = 2:1
B divides AC internally in the ratio 2 :1
Example
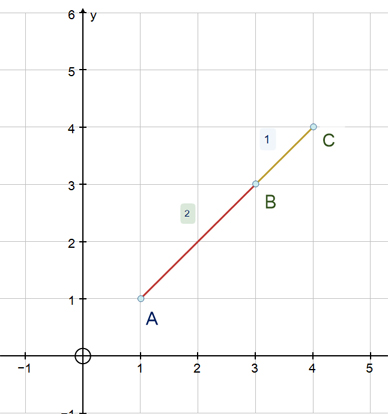
Given that the points A(1,1) , B(6,6 ) and C (4,4) are collinear , find the ratio in which B divides AC
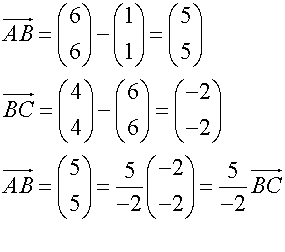
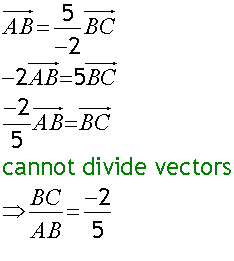
AB : BC = 5: -2
B divides AC externally in the ratio 5 : -2
Section Formula
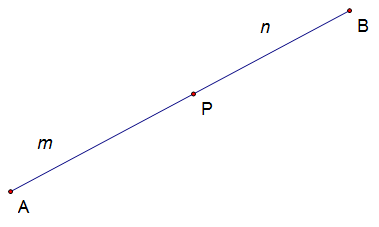
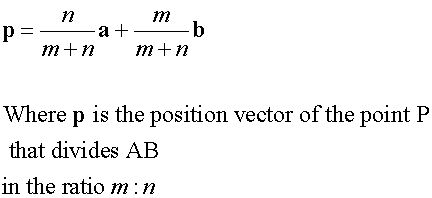
Why does this work ?
This example may help.
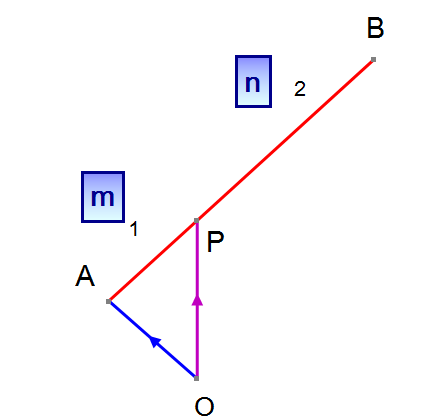
Take the points A and B and join them together with a straight line. Now let P be a point which cuts line AB in the ratio 1:2
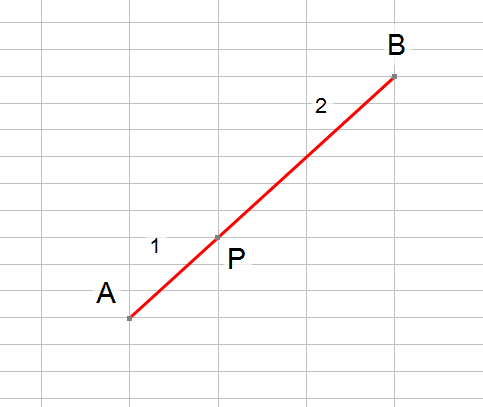
so that the length of AP is one half of the length PB
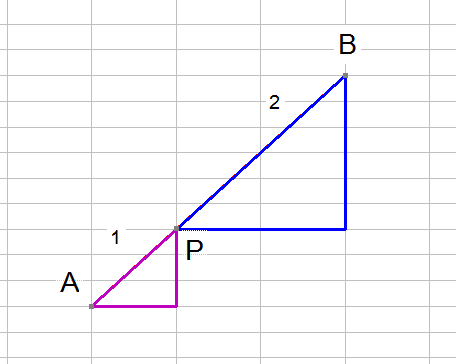
The points A and P can be represented by their position vectors.
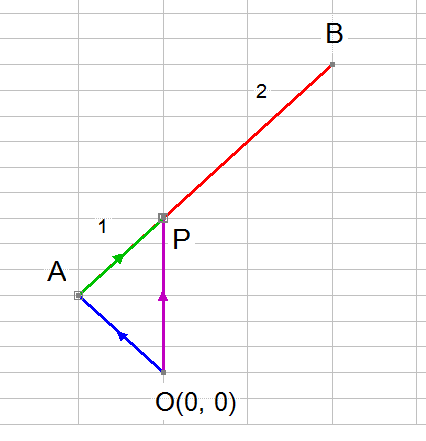
By vector addition,
![]()
Writing position vectors as vectors gives
![]() and
and ![]()
Since P splits AB in the ratio is 1:2
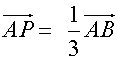
and
![]()
so
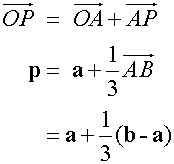
multiplying out the brackets
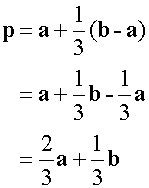
Notice that the numerator of a is 2 , which is the value of length n, and that of b is 1, which is the value of length m.
Also notice that the denominator of both is m+n.
so
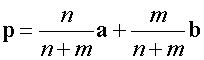
or if you prefer
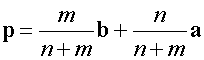
Example
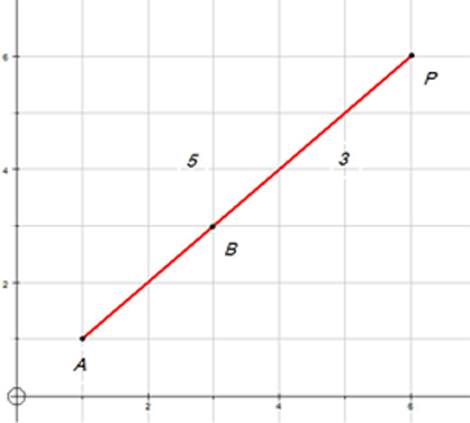
A and B have co-ordinates (6,7) and (16,22) respectively. Find the co-ordinates of the point P if AP:PB = 2:3.
Find the lengths of AB, AP and PB and check that the stated ratios are correct.
To find P
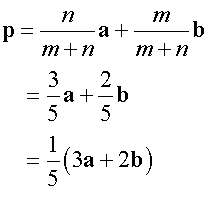
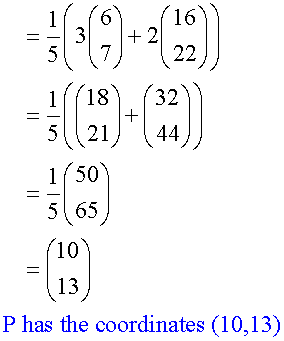
Alternatively
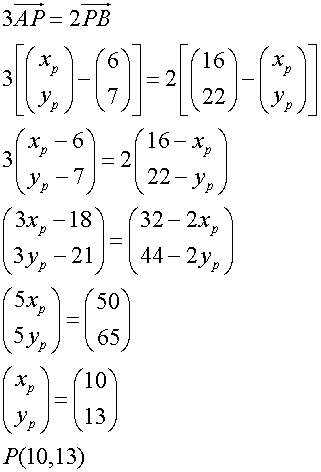
To find the lengths
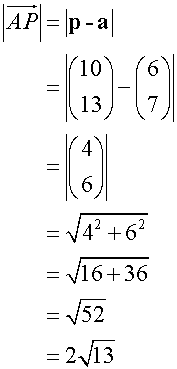
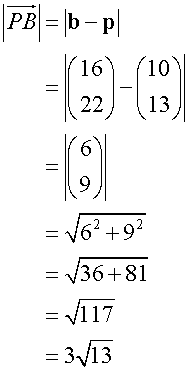
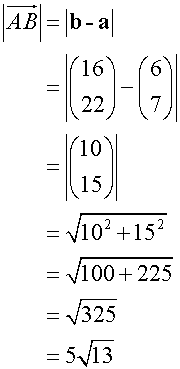
![]()
Looking at ratios
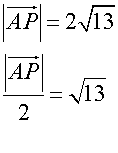
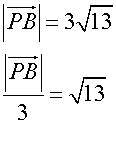
equating
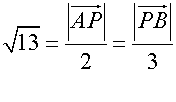
so
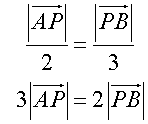
Ratio is given in form m : n
With split
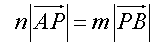
so
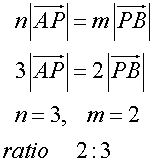
The stated ratios are correct.
Example
A and B have co-ordinates (1,1) and (3,3) respectively.Find the co-ordinates of the point P, which divides AB externally in the ration 5:3
Here, m = 5 and n = -3 , since it divides the line externally
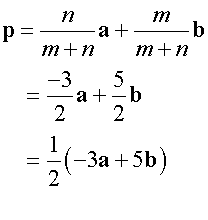
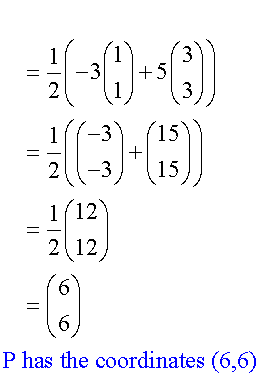
Scalar Dot Product
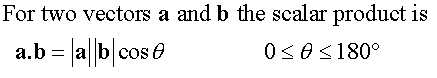
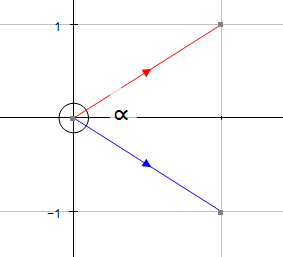
The angle required is always the angle formed when the vectors are both pointing towards or away from their intersection point.
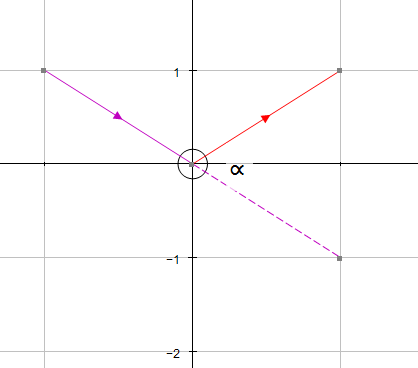
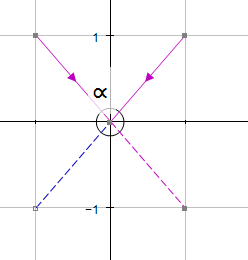
Example

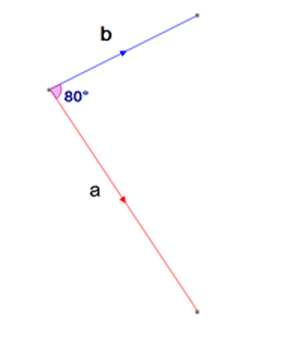
Examples
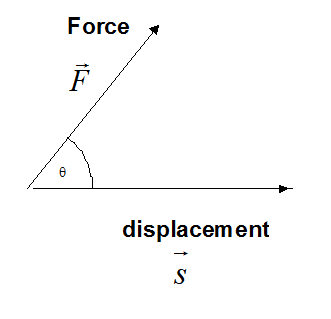
Work done by a constant force
![]()
Work is scalar, yet Force and displacement are vectors.
Power is the rate at which a force does work on an object.
If a force F does work W during a time interval Δt,
then the average power due to the force over the time scale is
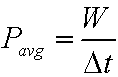
At any particular point of time ,
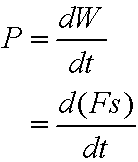
but the force is constant and
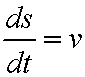
so
![]()
If the direction of the force is at an angle θ to the direction of travel of the object,
![]()
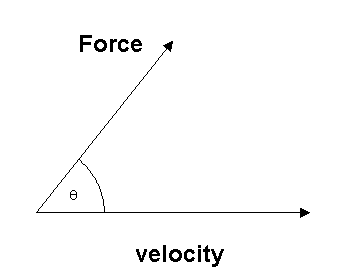
then instantaneous power is
![]()
Doggo decided to be lazy and accepted a lift from a pleasure boat.
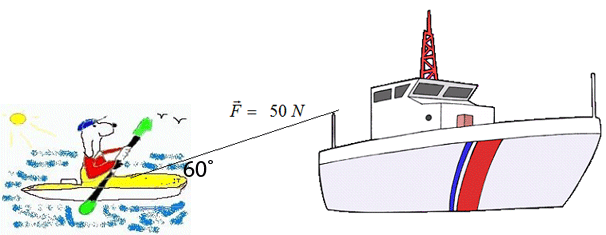
The tow rope exerts a force of 50 N on the kayak
at an angle 60˚ to the horizontal.
If the instantaneous power is 100 W, what is the magnitude of the
velocity of the kayak ?
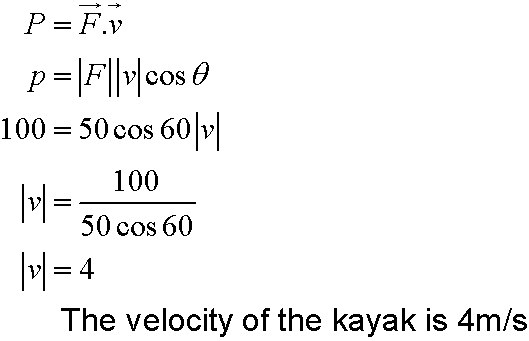
Component Form of Dot Product
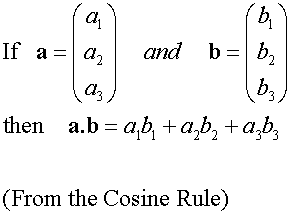
Examples
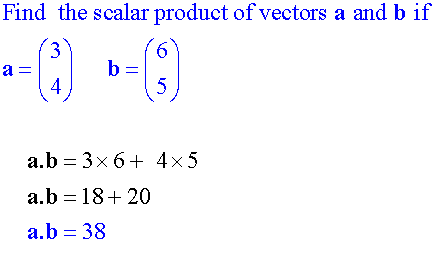
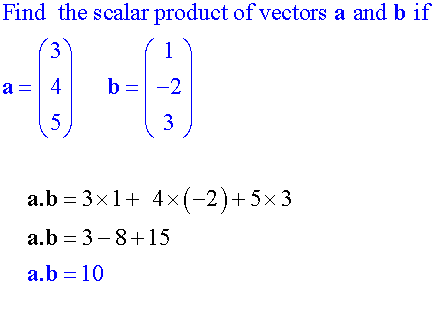
Angle between vectors
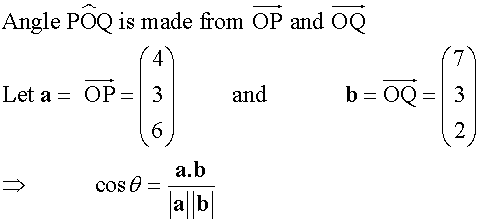
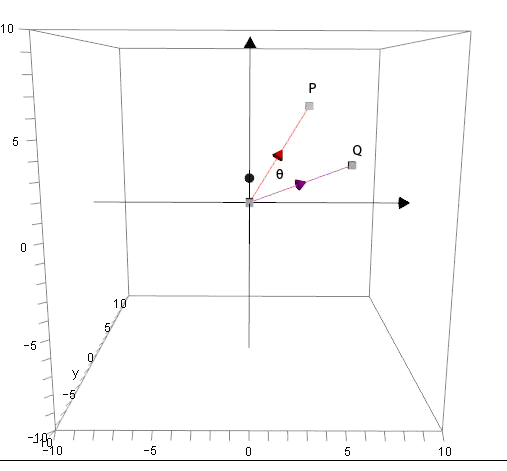
Place the vectors tail to tail
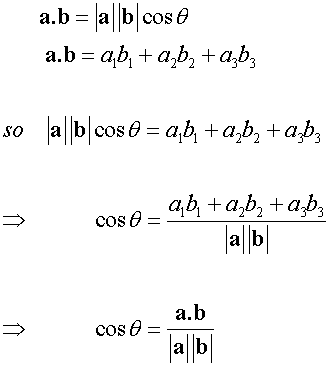
Example
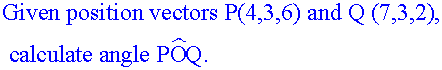
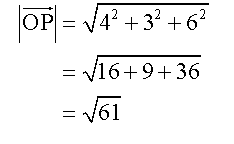
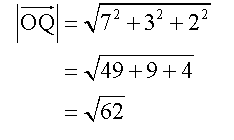
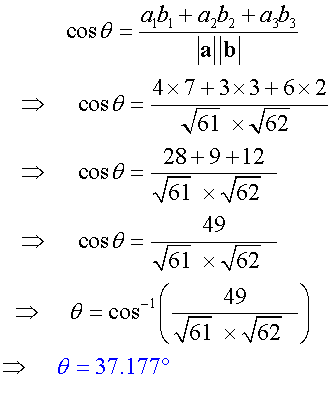
Which looks like this
Example
Calculate the angle,θ, between vectors
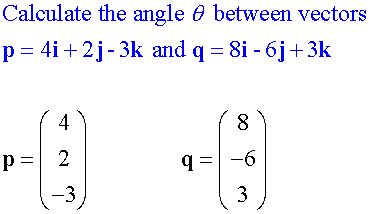
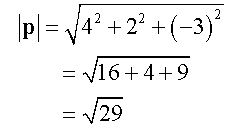
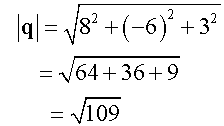
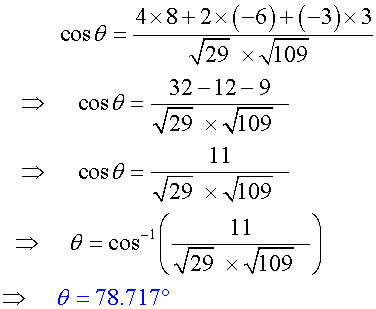
Perpendicular Vectors
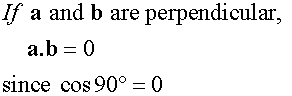
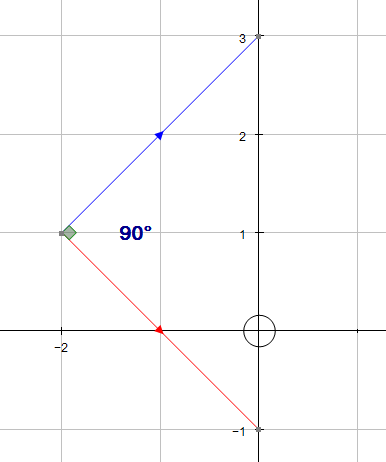
Example
Triangle ABC has co-ordinates A(5,7,-5), B(4,7,-3) and C (2,7,-4)
Is it right angled at B ?
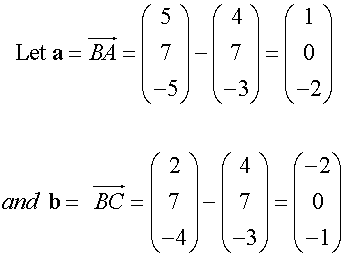
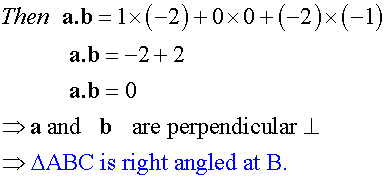
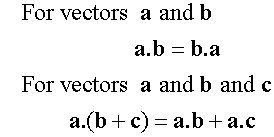
More Vectors
