This topic explains how to read and plot points in 2D and 3D, and how polar co‑ordinates work.
This grid method of describing direction and position is the work of the 17th‑century French philosopher and mathematician René Descartes.
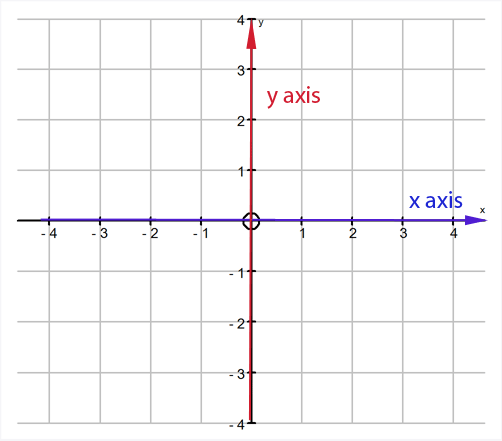
The x‑axis runs horizontally.
The y‑axis runs vertically.
They cross at the origin, \(O\).
Co‑ordinates are written as \((x, y)\), with the x‑value first.
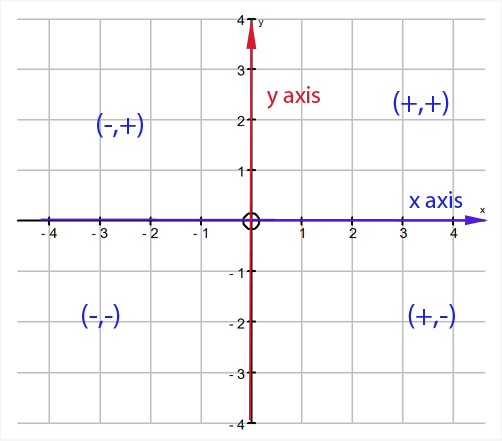
Points to the right of zero have positive x‑values.
Points above zero have positive y‑values.
Example
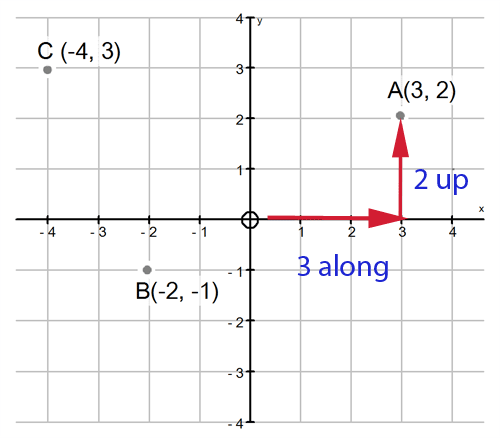
A is the point \((3, 2)\): 3 units along, 2 units up.
B is the point \((-2, -1)\): 2 units back, 1 unit down.
C is the point \((-4, 3)\): 4 units back, 3 units up.
Example
Plot the point \(G(3, -2)\).
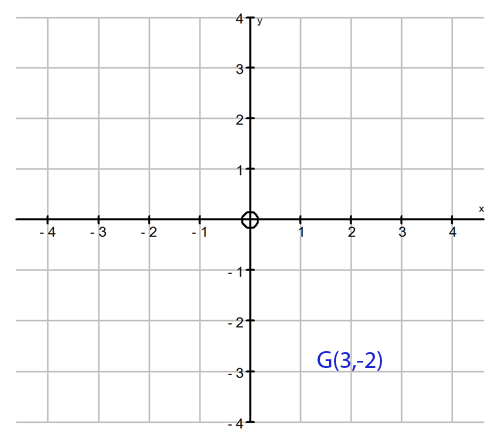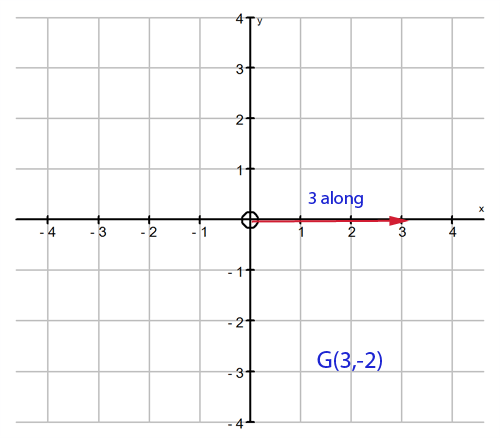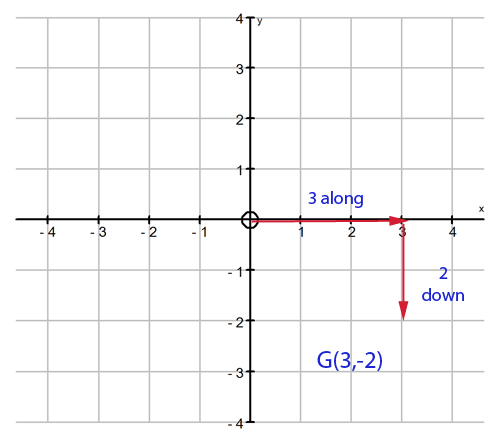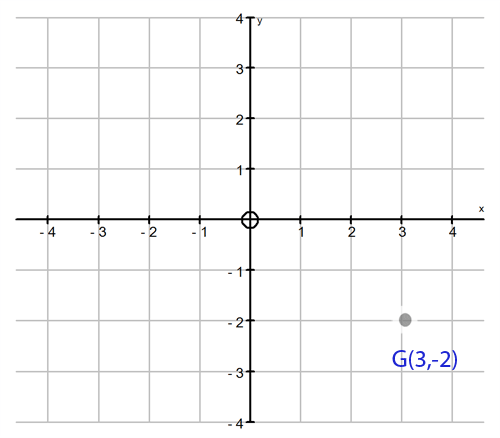
G is 3 units to the right and 2 units down.
Remember:
x along, y to the sky.
Along the corridor, then up the stairs.
In 3D:
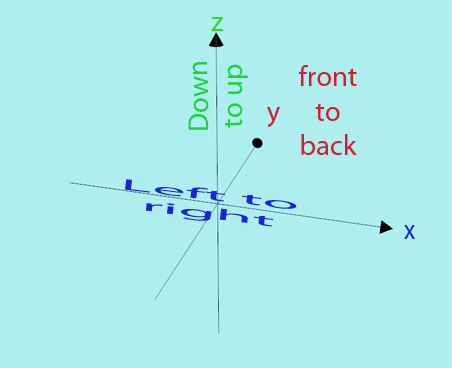
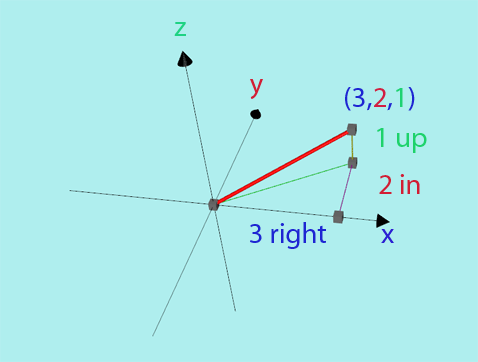
3D co‑ordinates are written as \((x, y, z)\).
Each point is identified by a length and an angle.
Polar co‑ordinates are written as \((r, \theta)\), where:
Examples
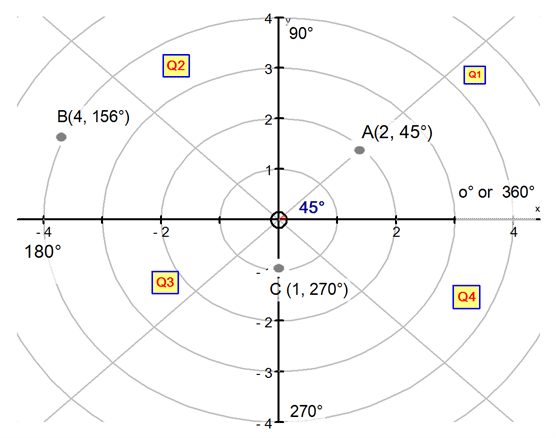
A has co‑ordinates \((2, 45^\circ)\): length 2, angle \(45^\circ\).
B has co‑ordinates \((4, 156^\circ)\): length 4, angle \(156^\circ\).
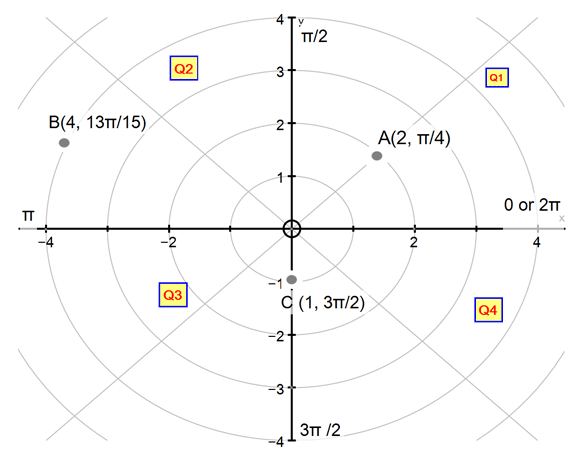
This is the same idea used in the CAST diagram for trigonometry.
© Alexander Forrest