Touching circles

Circles could touch internally,

 

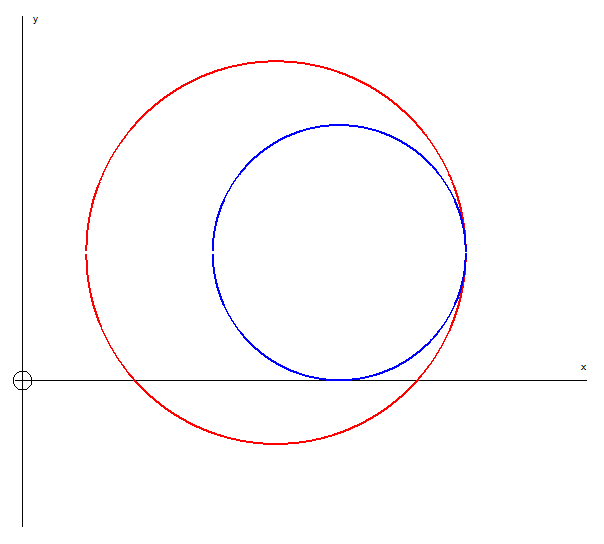
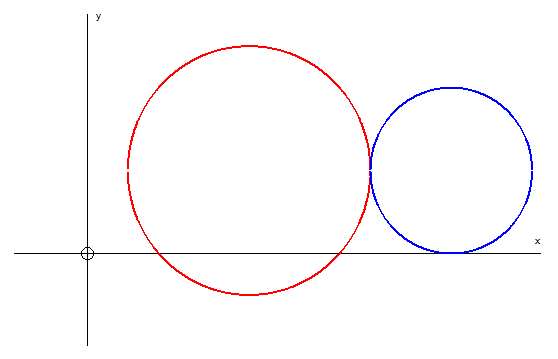
Externally,

 

 

 

 

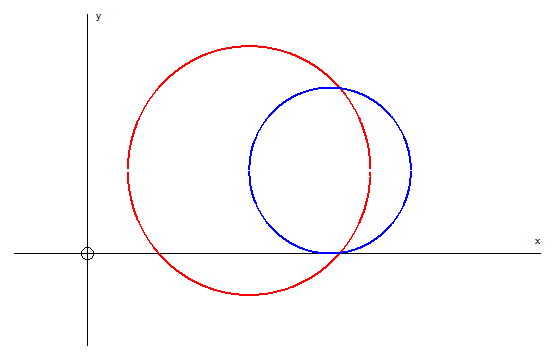
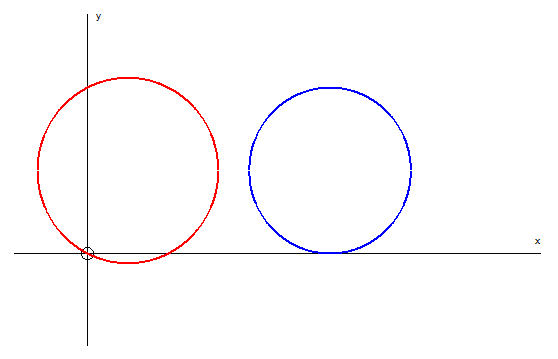
Or not at all

 

 

 

 

Do they touch ?

 

1. Find the distance between the centres.
2. Add the radii.
   If the result is the same, then the circles touch externally.
3. Subtract the radii
   If the result is the same, then the circles touch internally.

Example

Do the circles with equations

and

 touch ?

 

The first circle, C1, has centre A(-3 , 2)
 and radius 

The second circle, C2,has centre B(6, -1)
 and radius

Using the distance formula,

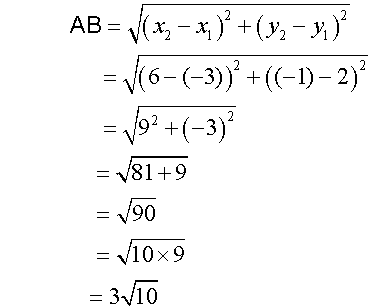
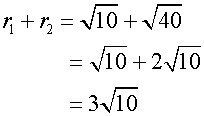
Since AB = r₁ +r₂, the circles touch externally.

 

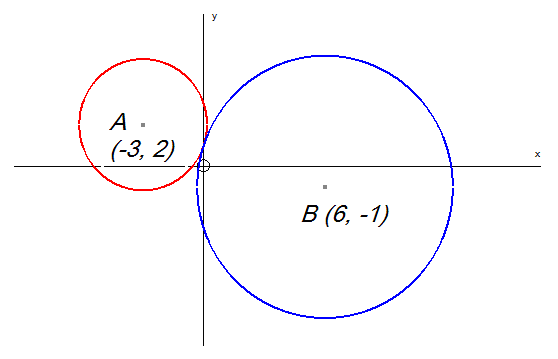
Example

Do the circles with equations

and

 touch ?

 

The first circle, C1, has centre A(4, 2)
 and radius r₁ = 3

The second circle, C2,has centre B(5, 2)
 and radius r₂ = 2

Using the distance formula,

      
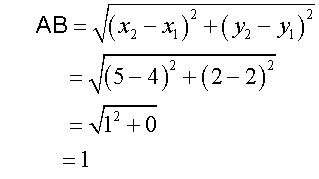
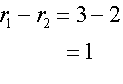
Since AB = r₁ - r₂, the circles touch internally.

 

Using points to find centres of touching circles

Example

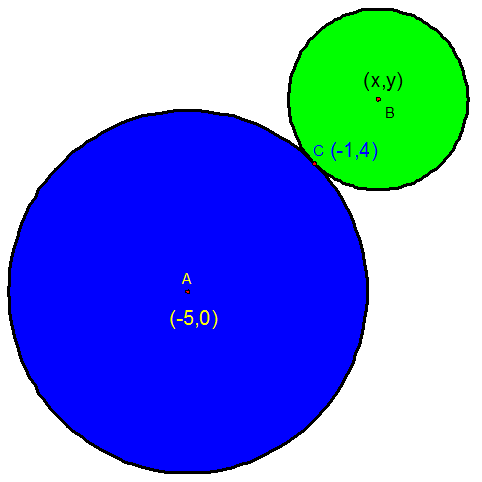
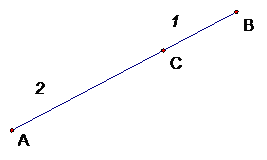
In the diagram below, the point C(-1,4) is the point of contact of the two circles.
Given that the radius of the larger circle is twice the size of the radius of the smaller circle, find the equation of the small circle.

Since C  is  point of contact for both circles,
distance AC must be the radius of the large circle
and CB the radius of the small circle.

 

Using the distance formula,

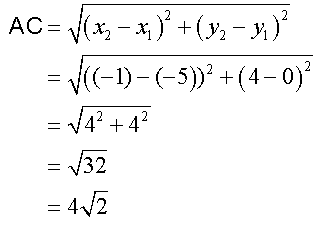
Given that AC =2CB

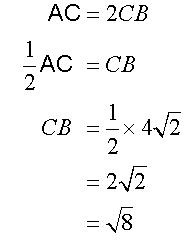
The centre of the smaller circle can be found by
finding the distances along and up for the larger
circle, halving these distances (since half the radius)
and applying to point C.

This is called the stepping out method.

From the distance formula for AC, (above)
the step out is 4 along and 4 up.

 

 

The next step out must be 2 along and 2 up
from point C.

Which gives the point B(1,6)

The equation of the small circle is

Using the Section Formula

Alternatively,using the section formula

gives

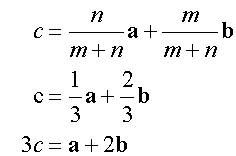
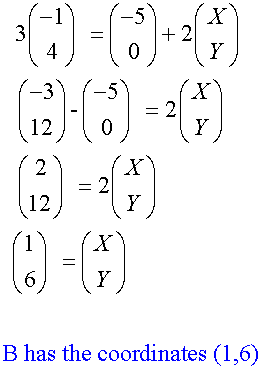
The equation of the small circle is