Definitions

Physical quantities usually fall into one of two categories:-  

Scalar   or   Vector

Scalars

A scalar quantity is defined totally by its magnitude (its size) and units.

A few scalars (not exhaustive)

• Distance
• Speed
• Time
• Temperature
• Energy
• Work
• Power
• Mass
• Volume
• Area

 

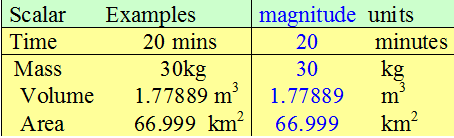
A speed of  60 mph is a scalar quantity.

Vectors

A vector quantity is defined totally by its magnitude, units and direction.

A few vectors (not exhaustive)

• Displacement
• Velocity
• Acceleration
• Force
• Weight

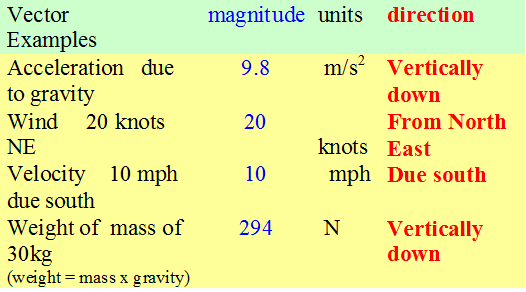
Speed is not a vector, since it doesn’t have a direction.

Velocity is a vector, so must have a direction.

Writing vectors

A vector  can be drawn as a line, with the length of the line  representing the magnitude and the direction indicated by an arrowhead.

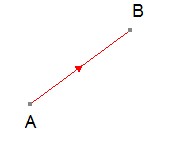
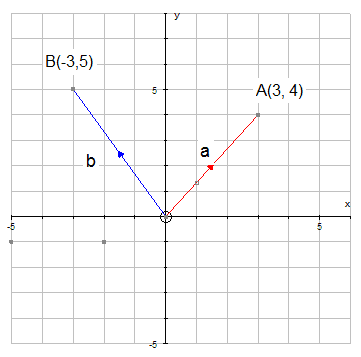
Vector AB is written as

The vectors below are shown in component form.

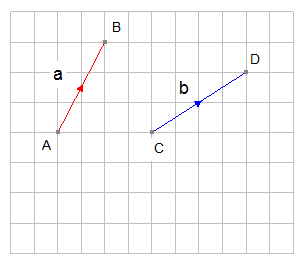
Vector AB is written as

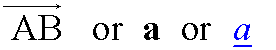
[Since you cannot write in your jotter in bold]

 

Notice that B is displaced 2 boxes to the right of A and 3 boxes up.

 i.e. 2 units in the x direction and 3 units in the y direction.

The components are written as a vector column

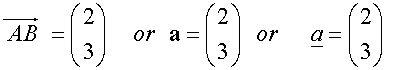
Likewise,

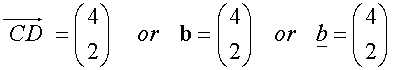
Column Vectors

When the  co-ordinates of the end points  are not known:-

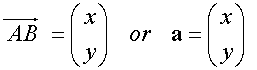
 Or in 3-D

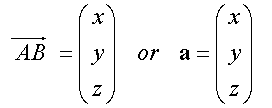
When the  co-ordinates of the end points  are known:-

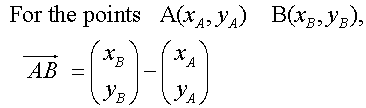
Or in 3-D

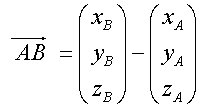
Examples

 

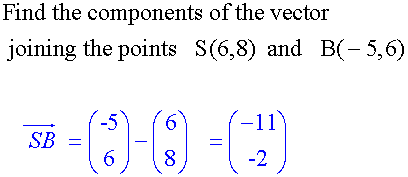
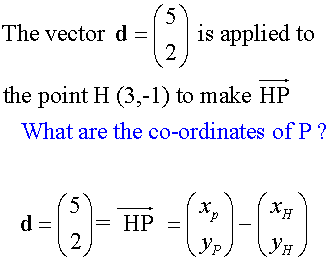
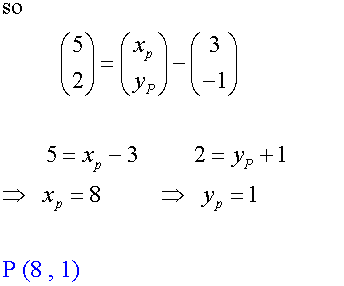
Equal Vectors

Each of these lines represent the vector

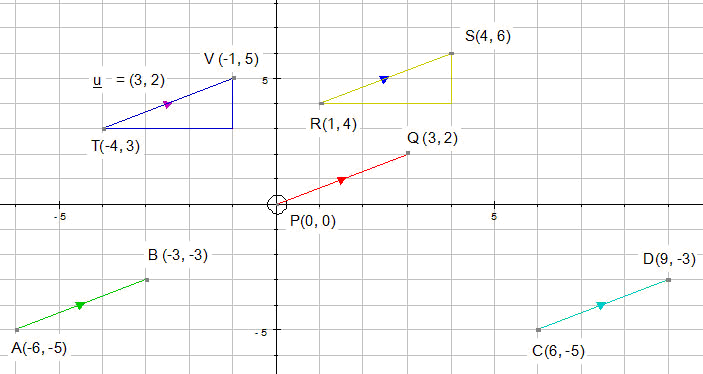
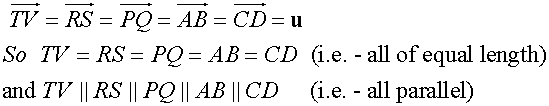
Direction is important

 

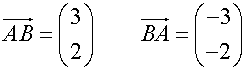
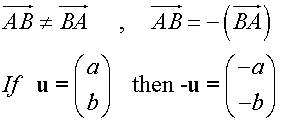
Magnitude

 A vector is always the hypotenuse of the right angled triangle formed by its x, y and z components. 

The magnitude of a vector is found by using Pythagoras’ Theorem.  

 

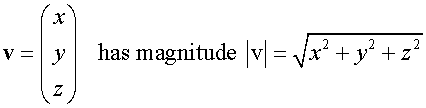
The magnitude is always a positive number !

Examples

Calculate the magnitude of each of the following vectors:-

 

 

 

 

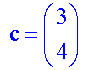
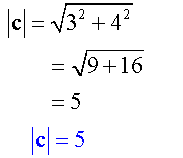
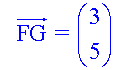
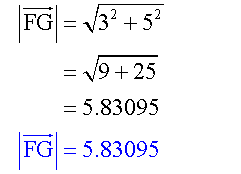
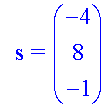
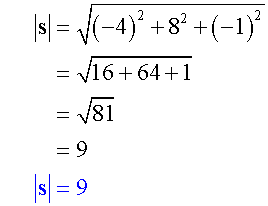
Example

Three points on a diagram have co-ordinates

P (3,4,-1)  Q (9,8,11)  and R (-9,-2,3)

Show that triangle PQR is isosceles

 

To be an isosceles triangle ,triangle  PQR  must have two sides of equal length.

Start by writing each column  vector.

          

    

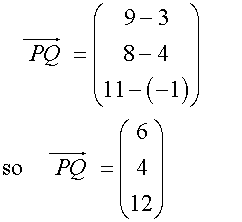
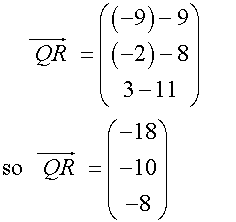
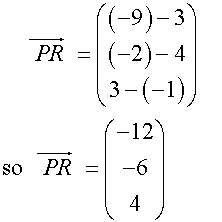
Find the magnitude of the vectors.

 

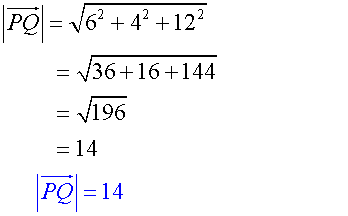
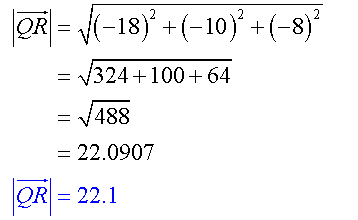
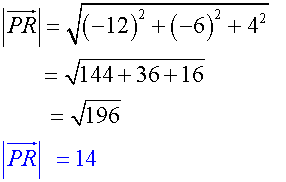
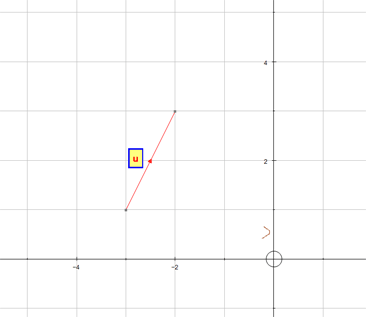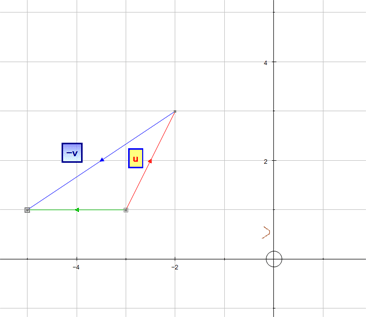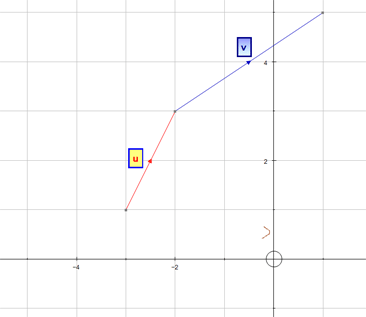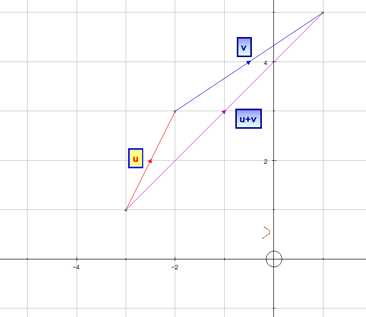
Adding Vectors

Vectors are added nose to tail,

to create an overall (resultant) vector.

 

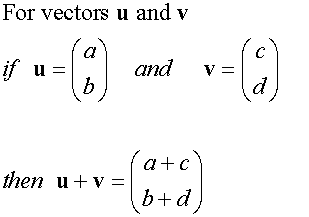
Example

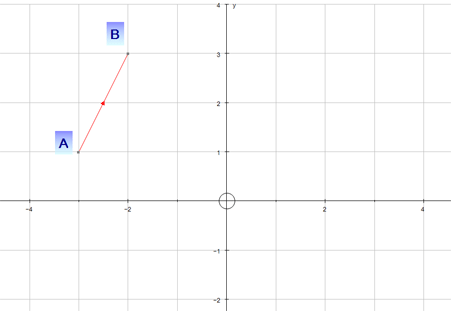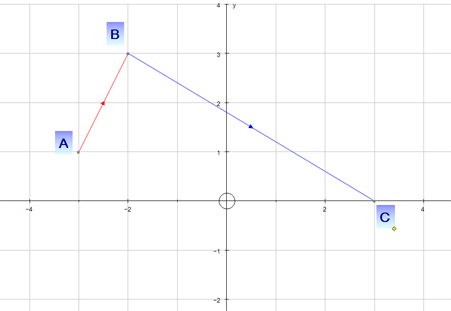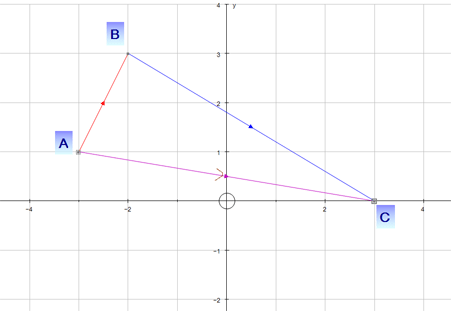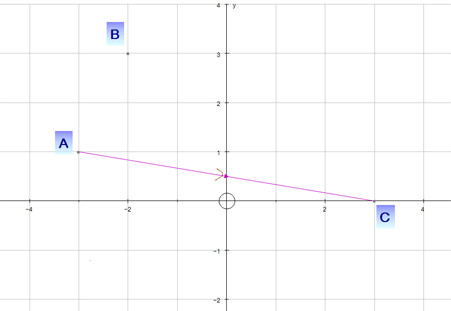
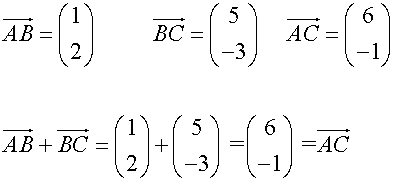
Example

 

 

 

 

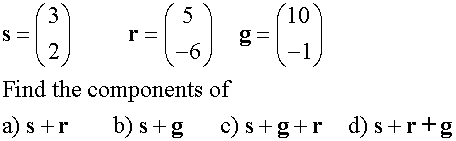
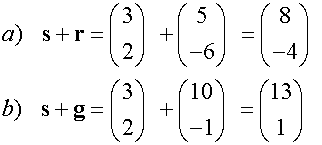
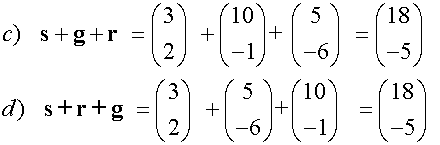
Subtraction of vectors

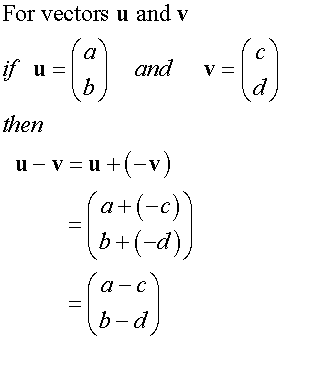
Example

 

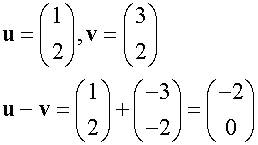
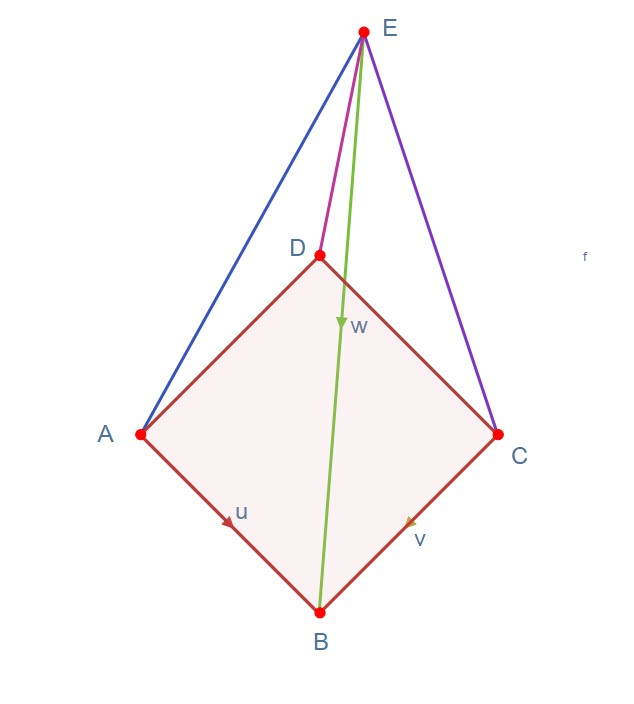
Vector paths

The shape below is a square based pyramid.

 

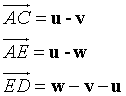
The Zero Vector

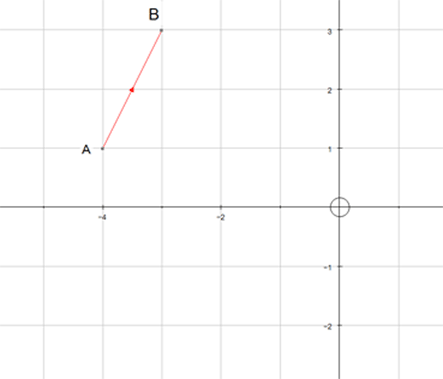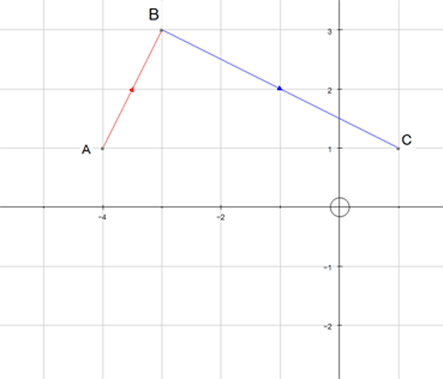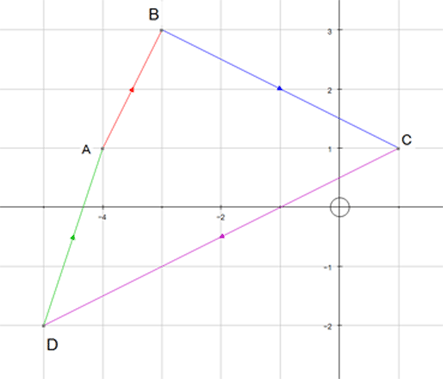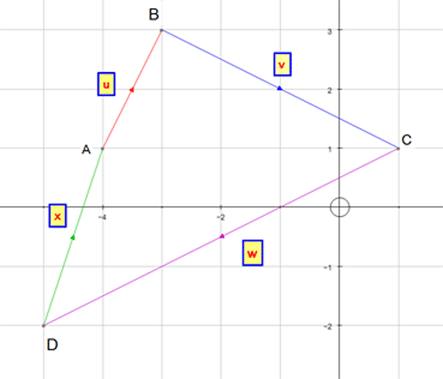
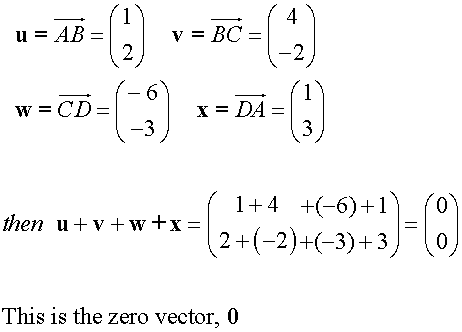
Note: Although travelling from A to B and back again has resulted in zero displacement from A, the distance travelled is the sum of the magnitudes.

 

Unit Vector

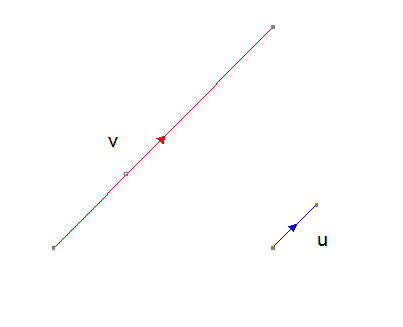
For any vector v, there is a parallel unit vector  of magnitude 1 unit.

Example

 

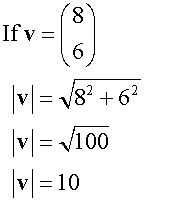
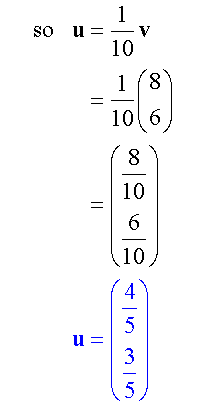
Position vector

A position vector is given relative to the Origin O.

 

 

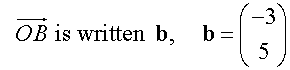
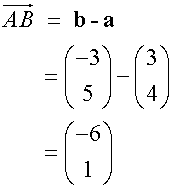
3 D Vectors

A vector may be described in terms of unit vectors i. j and k where

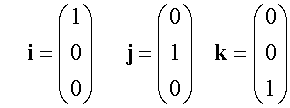
Example

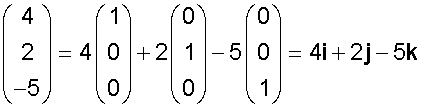
In General, the position vector of a point beginning at the origin and ending at point (x, y, z) is written

 

Multiplication of a vector by a Scalar

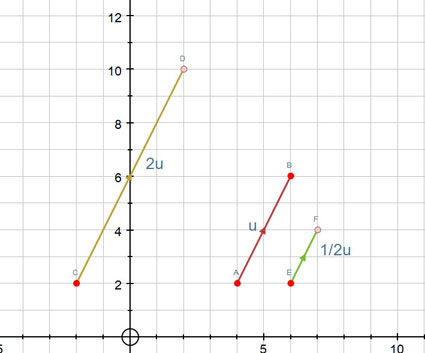
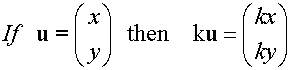
Example

 

 

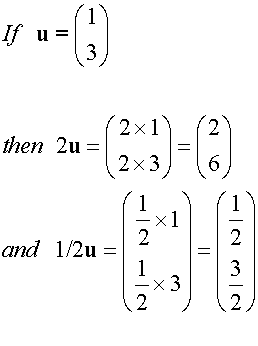
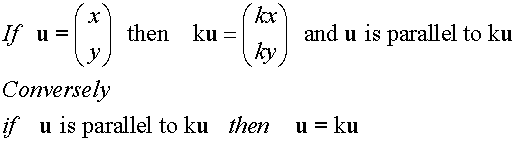
Collinearity

Example

Prove that the points A(1,1) , B(3,3 ) and C (4,4) are collinear and find the ratio in which B divides AC

 

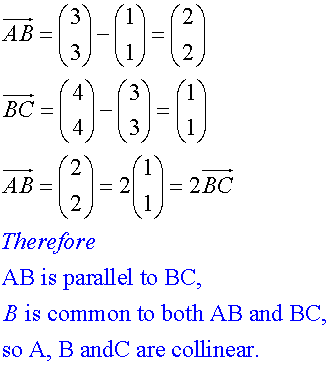
Ratio in which B divides AC

 

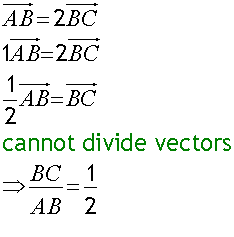
AB : BC = 2:1

B divides AC internally in the ratio 2 :1

 

Example

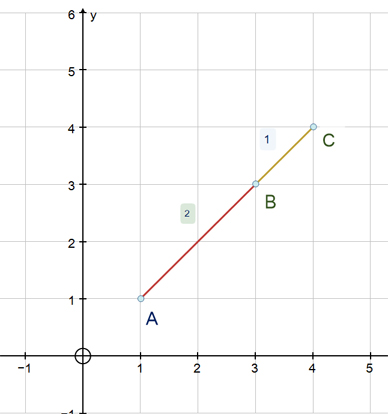
Given that the points A(1,1) , B(6,6 ) and C (4,4) are collinear , find the ratio in which B divides AC

 

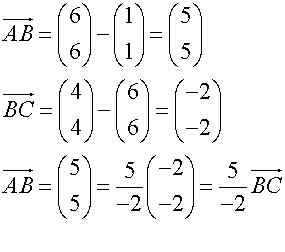
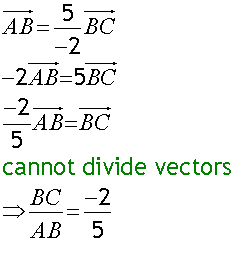
AB : BC = 5: -2

 

B divides AC externally in the ratio 5 : -2

 

 

Section Formula

   

    

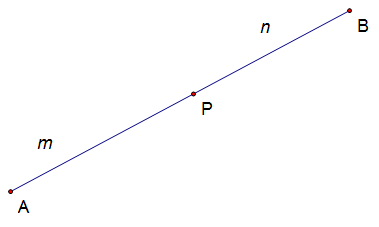
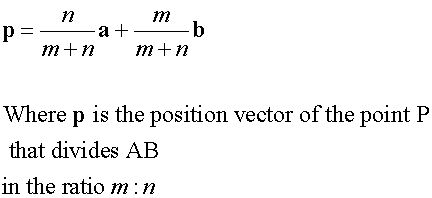
Why does this work ?

This example may help.

Take the points A and B and join them together with a straight line. Now let P be a point which cuts line AB in the ratio 1:2

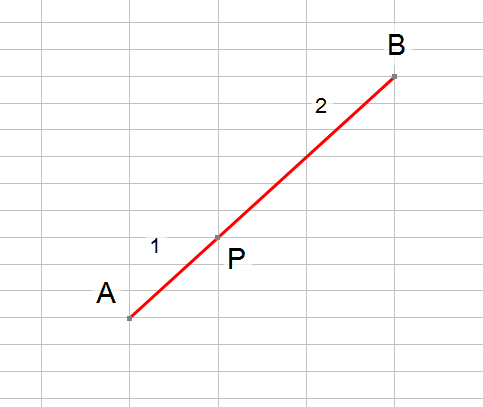
so that the length of AP is one half of the length PB

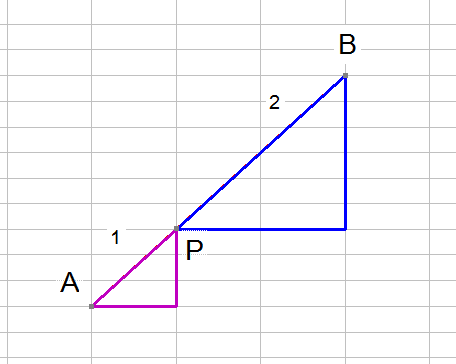
The points A and P can be represented by their position vectors.

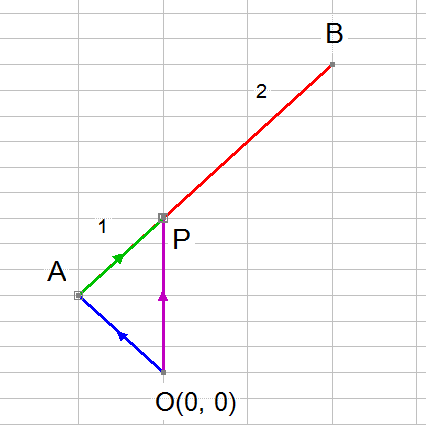
By vector addition,

Writing position vectors as vectors gives

and

Since P splits AB in the ratio is 1:2

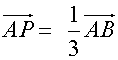
and

so

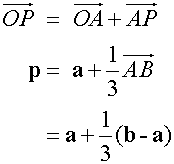
multiplying out the brackets

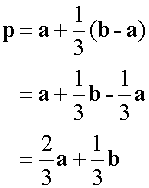
Notice that the numerator of a is 2 , which is the value of length n, and that of b is 1, which is the value of length m.

Also notice that the denominator of both is m+n.

 

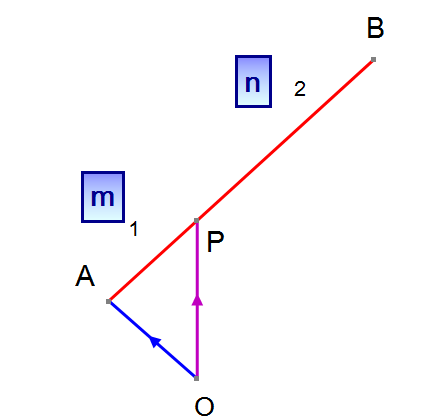
so

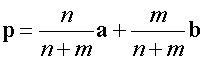
or if you prefer

 

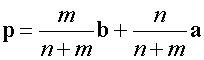
Example

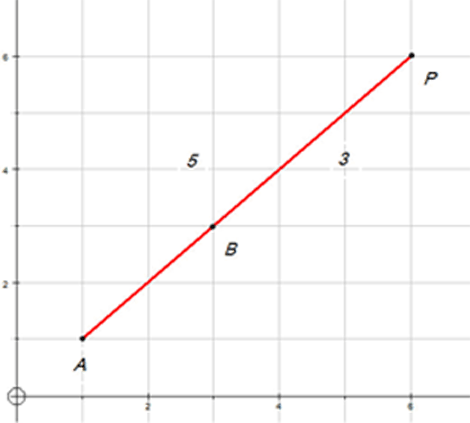
A and B have co-ordinates (6,7) and (16,22) respectively. Find the co-ordinates of the point P if AP:PB = 2:3.

Find the lengths of AB, AP and PB and check that the stated ratios are correct.

 

 

To find P

 

 

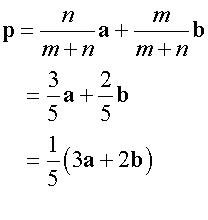
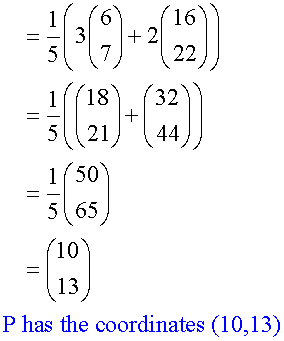
Alternatively

 

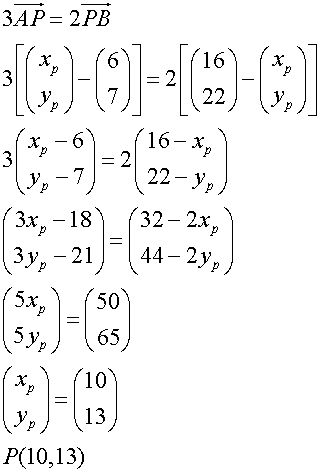
To find the lengths

 

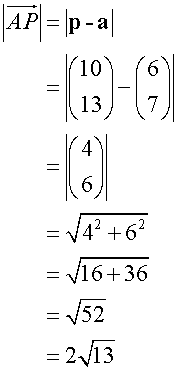
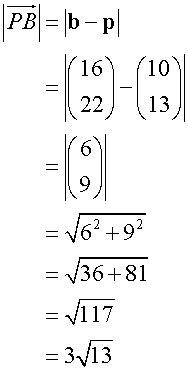
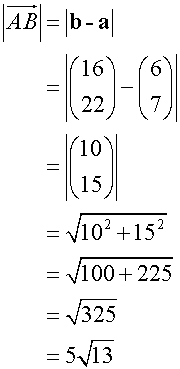
Looking at ratios

 

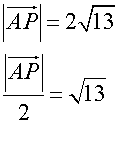
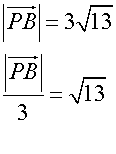
equating

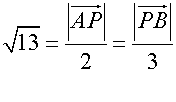
so

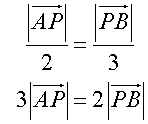
Ratio is given in form m : n

With split

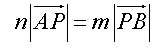
so

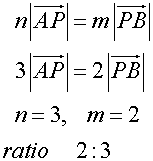
The stated ratios are correct.

 

Example

A and B have co-ordinates (1,1) and (3,3) respectively.Find the co-ordinates of the point P, which divides AB externally in the ration 5:3

Here, m = 5 and n = -3 , since it divides the line externally

 

 

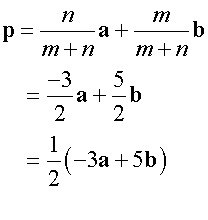
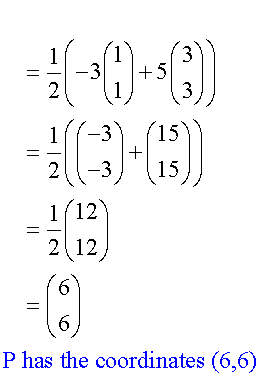
Scalar Dot Product

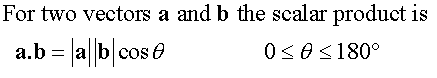
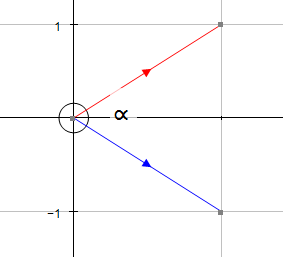
The angle required is always the angle formed when the vectors are both pointing towards or away from their intersection point.

 

 

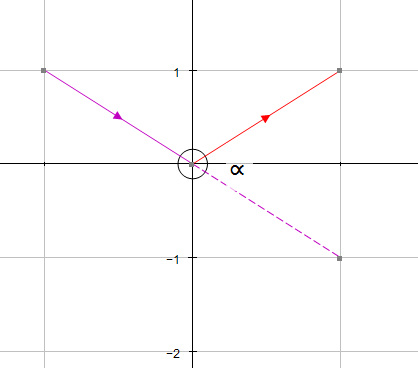
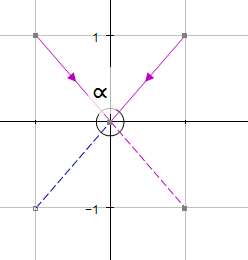
Example

 

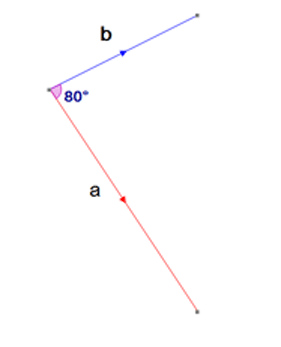
Examples

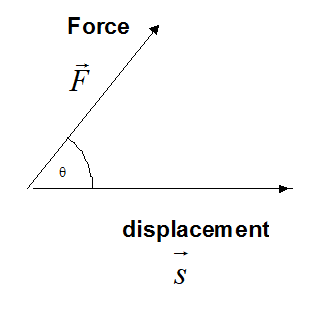
Work done by a constant force

Work is  scalar, yet Force and displacement are vectors.

 

Power is the rate at which a force  does work on an object.

If a force F  does  work W during  a time interval Δt,

then the  average power due to the force over the time scale is

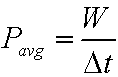
At any particular point of time ,

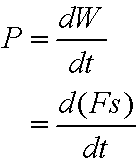
but the force is constant and

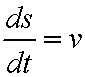
so

If the direction of the force is at an angle  θ to the direction of travel of the object,

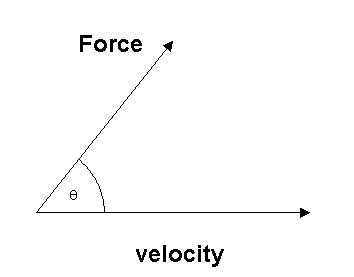
then instantaneous power is

Doggo  decided to be lazy and accepted a lift from a pleasure boat.

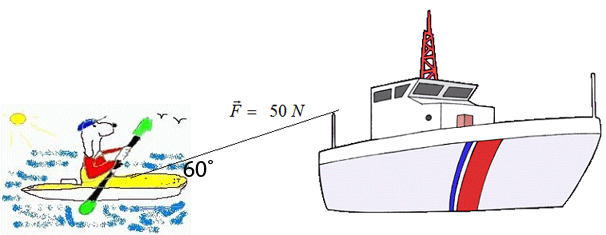
  The tow rope exerts a force of  50 N on the kayak
 at an angle 60˚ to the horizontal.

If the instantaneous power is 100 W, what is the magnitude of the
velocity of the kayak ?

 

 

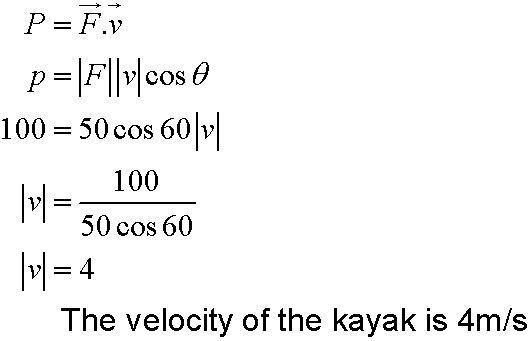
Component Form of Dot Product

 

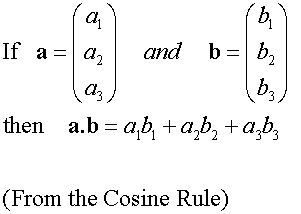
Examples

 

 

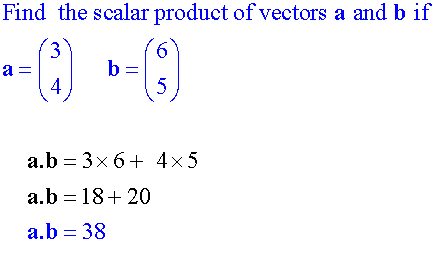
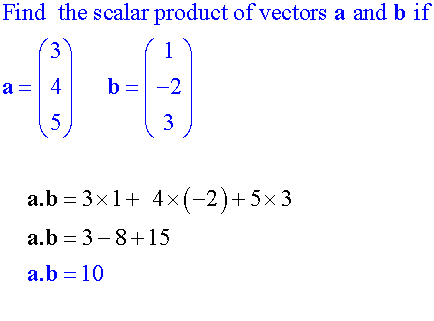
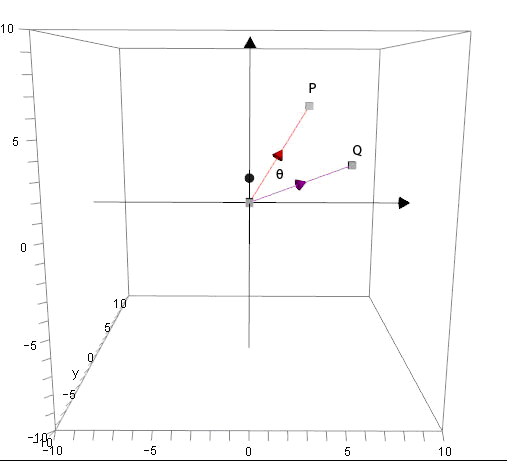
Angle between vectors

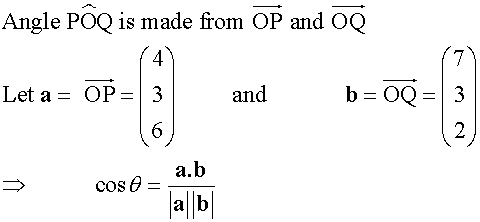
Place the vectors tail to tail

 

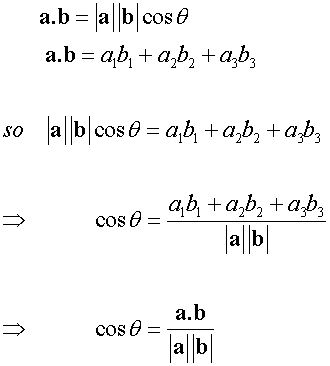
Example

 

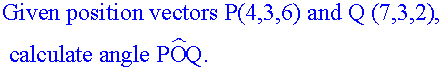
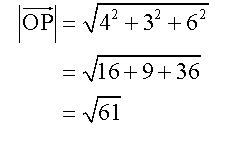
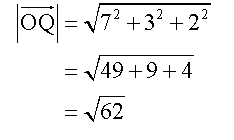
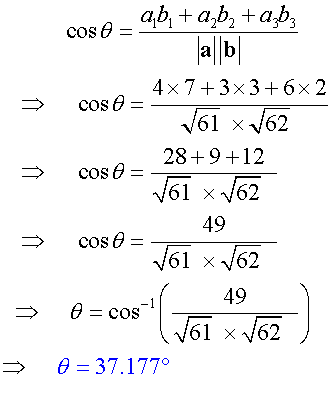
Which looks like this

 

 

Example

Calculate the angle,θ, between vectors

 

 

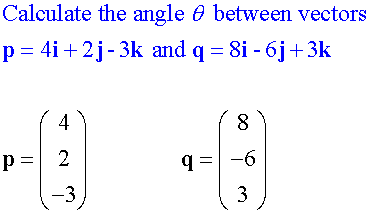
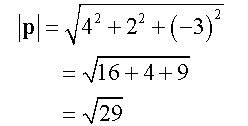
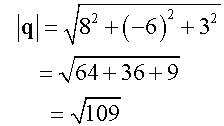
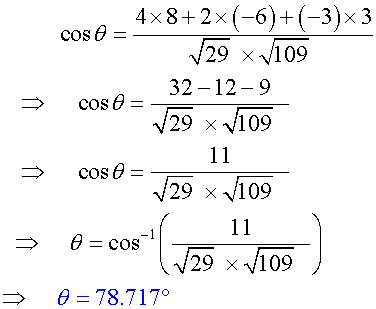
Perpendicular Vectors

 

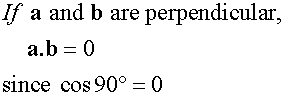
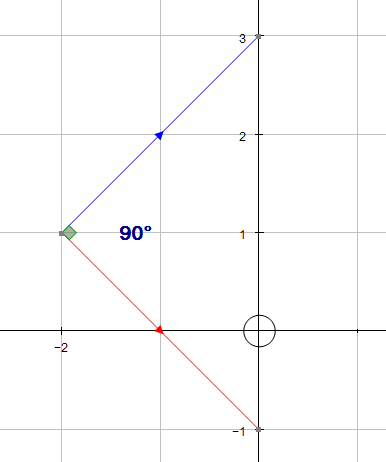
Example

Triangle ABC has co-ordinates A(5,7,-5), B(4,7,-3) and C (2,7,-4)

Is it right angled at B ?

 

  

 

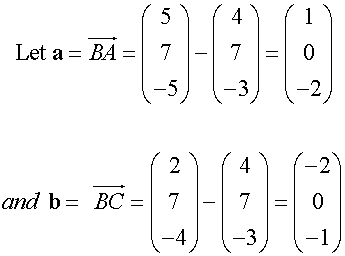
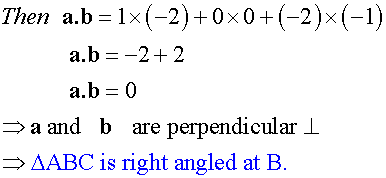
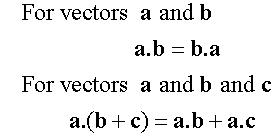
More Vectors