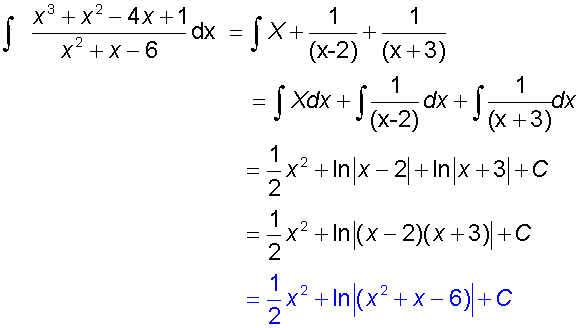Partial Fractions

Proper rational functions

A proper rational function is one in which
the degree of the numerator is less than
that of the denominator.

 eg.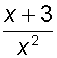   

All others are termed improper.
These can be simplified through long division.

Example

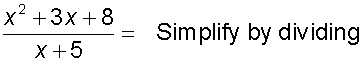
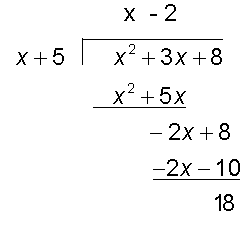
so

 

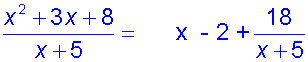
General Forms

 

 

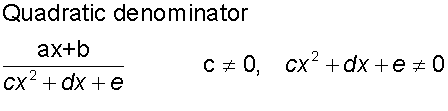
Partial Fractions

Partial fractions are decomposed components of a fraction

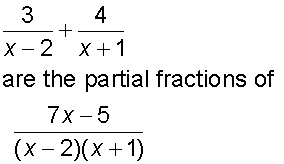
since

 

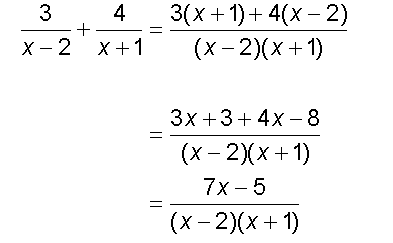
The steps taken to find the partial fractions depend on the original function

 

Distinct linear factors

Example

   

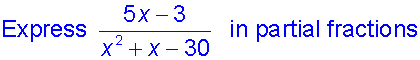
First,write the denominator in factorised form:

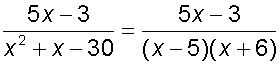
Now set this equal to two partial fractions

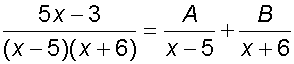
Thus

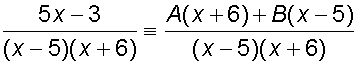
This is an identity,

so A and B can be found by comparing co-efficients

Now pick values of x to find A and B

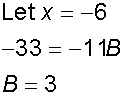
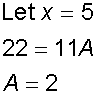
Substitute back into equation

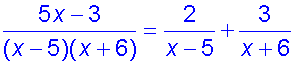
Repeated linear factor

Example

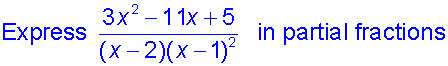
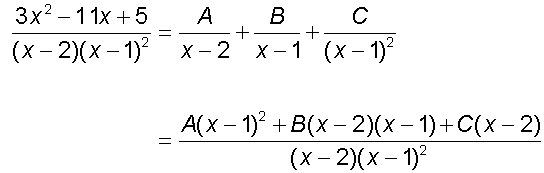
so

comparing co-efficients

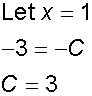
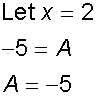
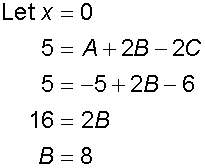
giving

 

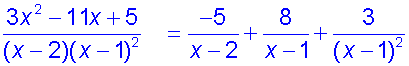
Irreducible quadratic factor

This occurs if the discriminant of the denominator is less than zero.

Example

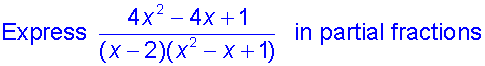
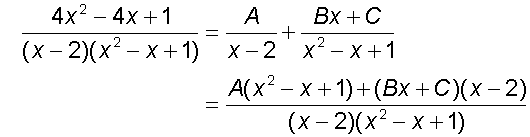
so

comparing co-efficients

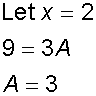
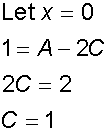
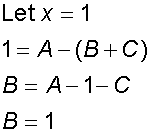
giving

 

 

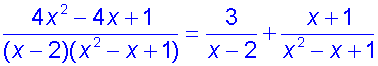
Rules

 

The degree of the numerator must be lower than than that of the denominator. If not, divide!

 

 

 

 

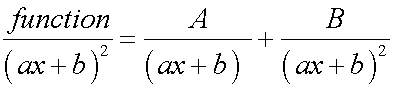
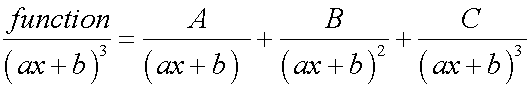
Example

 

 

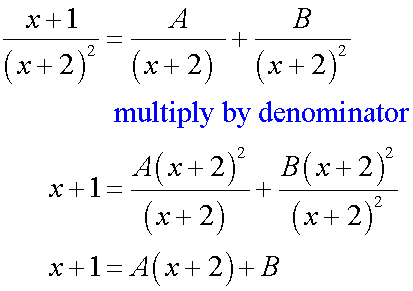
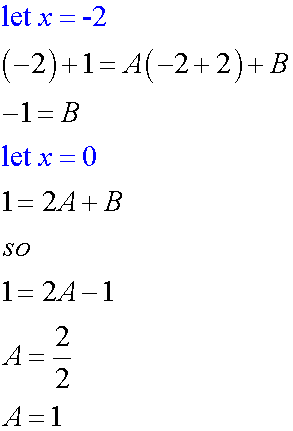
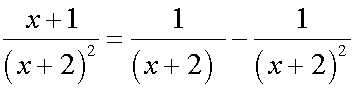
Integrating rational functions

 

Example

Find the  integral

 

 

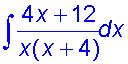
First, find the partial fractions

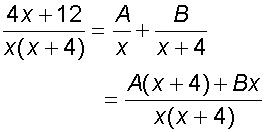
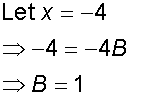
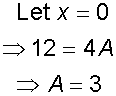
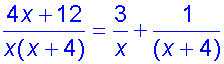
Now integrate

   

 

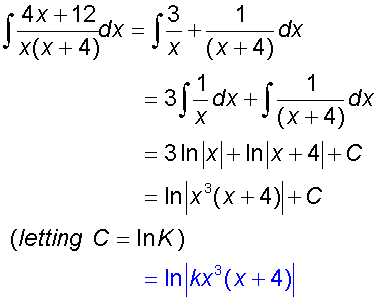
Example

Find the  integral

 

       

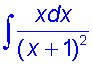
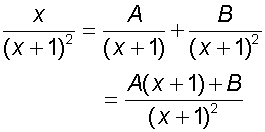
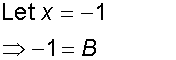
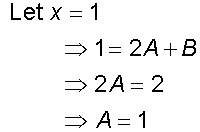
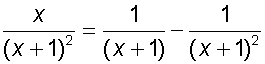
Now integrate

     

 

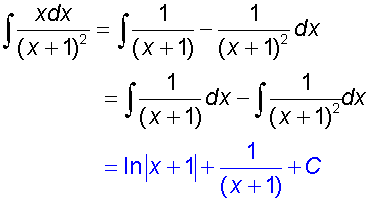
Example

Find the  integral

      

    

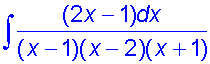
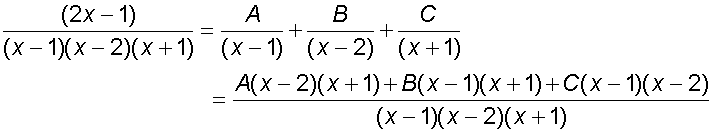
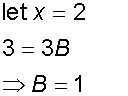
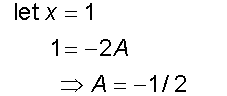
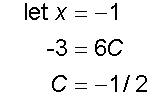
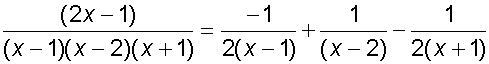
Now integrate

 

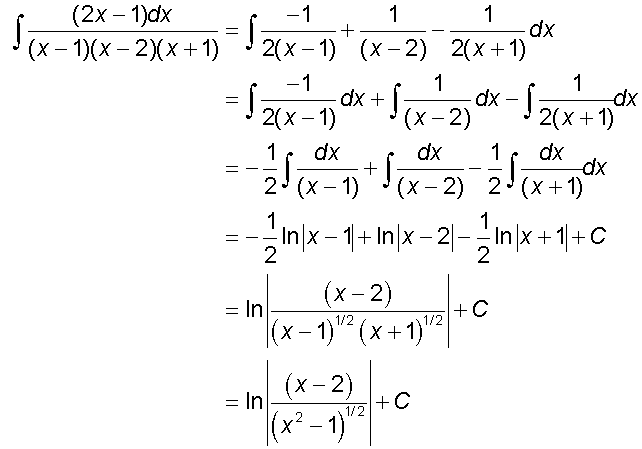
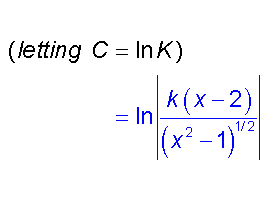
Example

Find the  integral

   

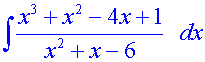
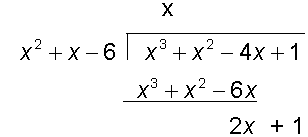
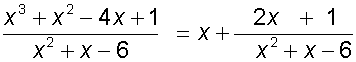
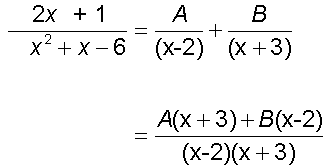
so

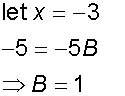
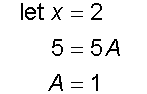
giving

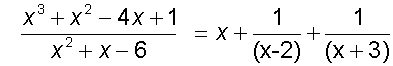
Now integrate