Newton’s equations of Motion:-

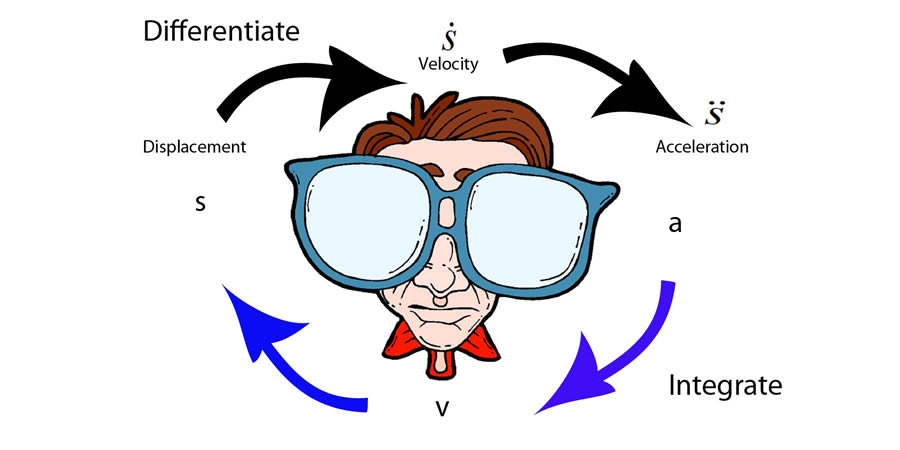
Deriving the equations of motion

 

         

 

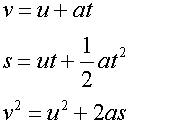
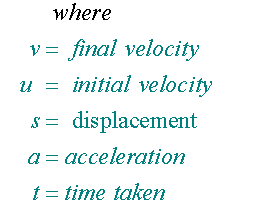
Re-arranged

 

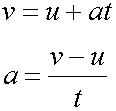
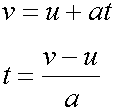
When starting from rest u = 0

giving

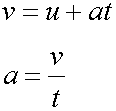
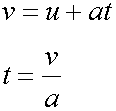
Rearranging the second formula:

 

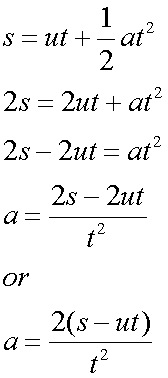
When u = 0,

 

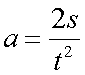
Rearranging the second formula for time :

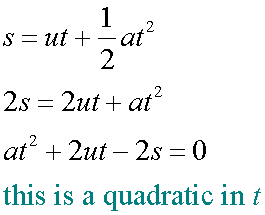
When u = 0 ,

 

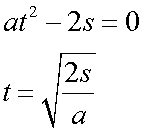
Otherwise

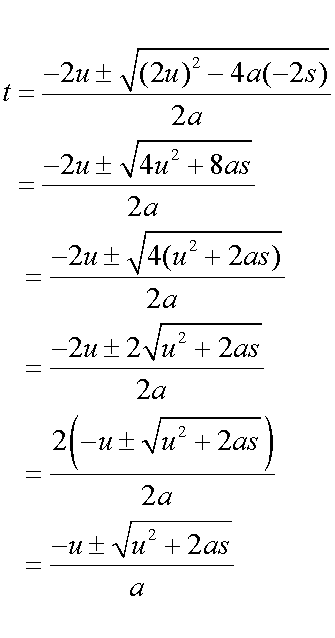
Rearranging the third formula:

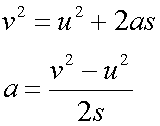
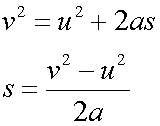
When u = 0 ,

 

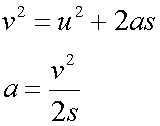
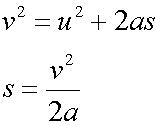
Notice that

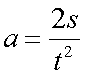
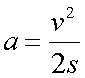
so when u = 0

 

 

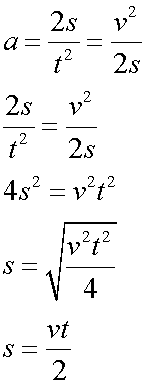
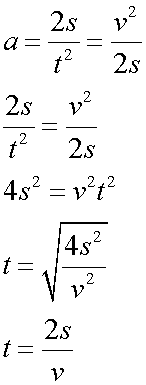
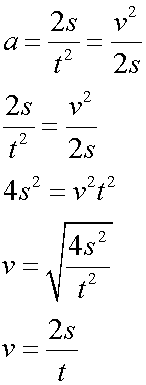
Integrating methods

 

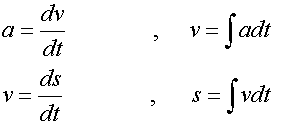
Displacement , s, is the vector quantity of the distance travelled from a fixed point.

After time ,t,  the displacement from the origin
can be written as the function s(t).

A particle in motion on a plane at position (x(t),y(t))  at time t
can be represented by the position vector

where i and j are unit vectors in the x and y directions.

The distance from the origin is the magnitude
of the displacement

 

 

Velocity is the rate of change of displacement with  respect to time .

 

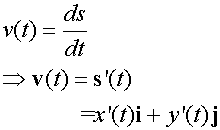
This is often shortened to

  

The speed of the particle at time t is found using the equation

The direction of motion at time t is

 

 

 

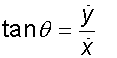
Acceleration is the rate of change of velocity with  respect to time .

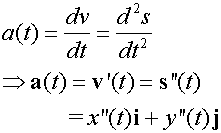
 This is often shortened to

The magnitude of acceleration at time t
is found using the equation

The direction of acceleration at time t is

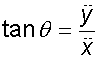
Example

A particle moving in a plane such that its displacement
is given by the equations

x = 3t³ + 2t²     and y = 4t² + 5t  

(x and y are measured in metres , time is in seconds)

Find, when t = 2,

1. the position of the particle.
2. the magnitude and direction of its velocity
3. the magnitude and direction of its acceleration

Solution

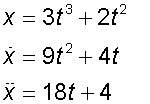
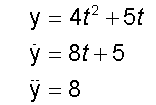
1.    when t = 2,

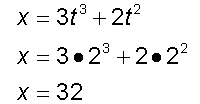
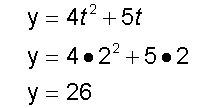
The particle is at (32,26)

 

2. when t = 2,

 

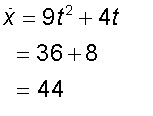
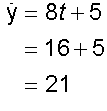
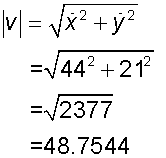
The speed is 48.8m/s

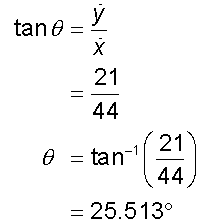
The velocity is 48.8 m/s at a direction
of 25.5° from the horizontal.

 

3.

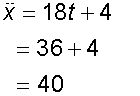   and

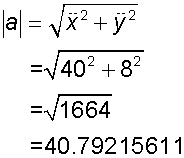
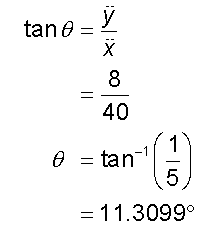
The acceleration is 40.8 m/s²
at a direction of 11.3° from the horizontal.