Mathematical Modelling
Mathematical modelling help solve real-world problems through finding relationships between variables that specify the issue being examined.
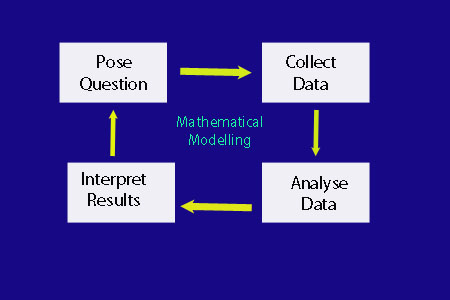
Once a question is posed, data is collected, analysed and then interpreted to look for any patterns or relationships that could be used to see if the model works and make predictions useful for real-life situations.
This is often an iterative process - it is tweaked and repeated until an acceptable outcome is reached.
Modelling Stages
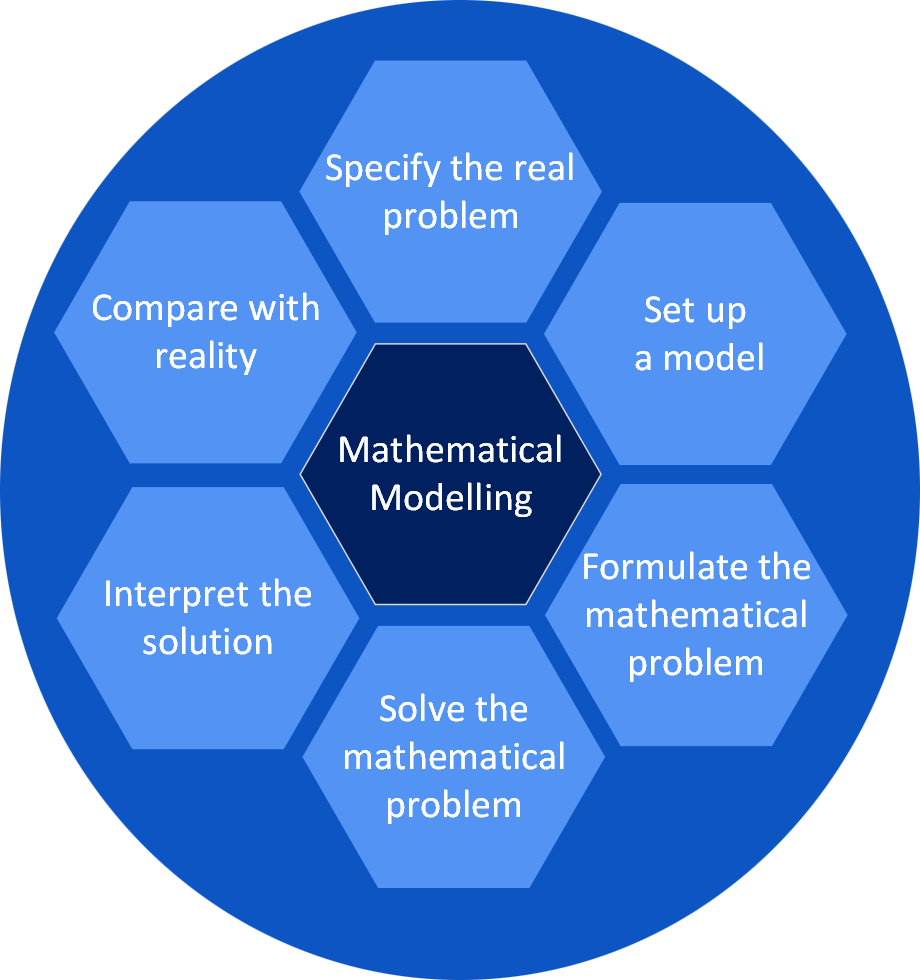
1. Specify the real problem
- What exactly is the problem the model needs to address ?
- Simplify the problem and identify its most important features.
2. Set up a model
- Specify assumptions
- Choose appropriate variables
- Specify relationships
- Specify any parameters
- Specify data to be collected
3. Formulate the mathematical problem
- Identify the dependant variable
- Write down relevant potential formulae
- A sketch can be helpful
- Recurrence relationship?
- Differential equation ?
- Optimization problem ?
4. Solve the mathematical problem
- Use relevant skills
5. Interpret the solution
- What do the results mean ?
- Do graphs show any relationships ?
- Any useful equations formulated ?
6. Compare with reality
- Try some data to see if the model works
- Is it realistic ?
- What improvements can be made ?
Example
A person wishes to buy a car with an unsecured bank loan.
- £550 is available for monthly loan repayments.
- The loan can last 3,4 or 5 years.
What is the top of the car price range that is affordable?
1. Specify the real problem
How much of a loan can be acquired for a monthly repayment of £550 ?
The amount to be borrowed depends on the interest rate and term of the loan.
2. Set up a model
Interest rates vary between loan companies, so a selection of rates will be considered for loan terms of 3, 4 and 5 years :
| Lender | Annual Rate |
|---|---|
| Online loan company A | 61.94% representative. |
| Online loan company B | 19.9% representative. |
| Own Bank | 6.2% |
It is assumed that the loan will be taken out at the representative rate, fixed for the duration term of the loan.
The variables will be the interest rate and number of repayments.
The number of monthly repayments will be 36 , 48 or 60
The total monthly repayment must not exceed £550 .
First go around
3. Formulate the mathematical problem
As a basic first step, assume that the monthly payments were put aside into an account.
The balance of the account would be
- £550 x 36 = £19,800 after 3 years
- £550 x 48 = £26,400 after 4 years
- £550 x 60 = £33,000 after 5 years
The account balance equals the interest paid and the original capital borrowed.
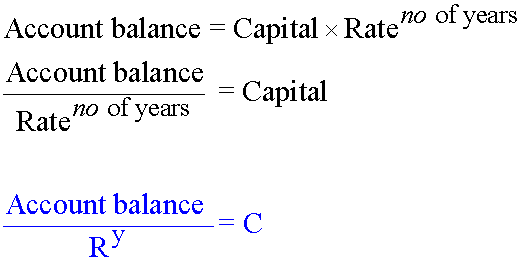
4. Solve the mathematical problem
Online loan company A , interest rate 61.94% per year
3 years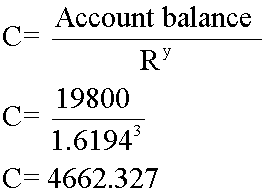 
£4,662.33
4 years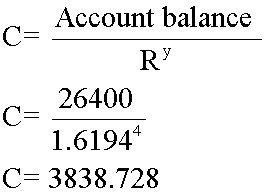 
£3,838.73
5 years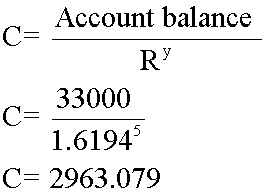 
£ 2,963.08
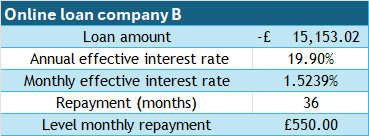
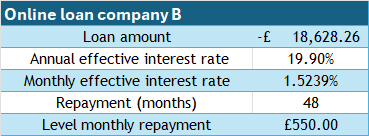
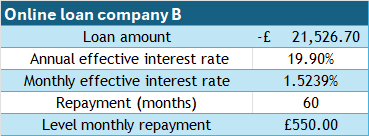
Online loan company B , interest rate 19.9% per year
3 years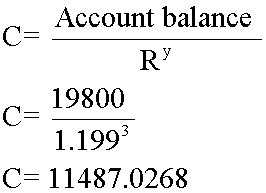 
£11,487.03
4 years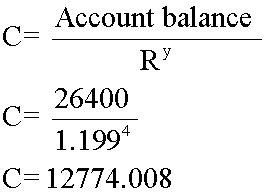 
£12,774.01
5 years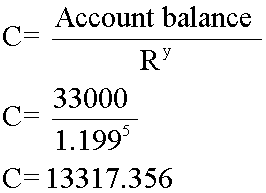 
£13,317.36
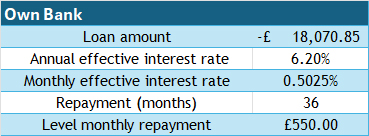
Own Bank, interest rate 6.2% per year
3 years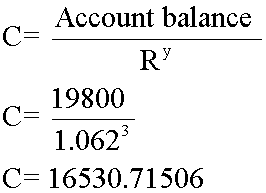 
£16,530.72
4 years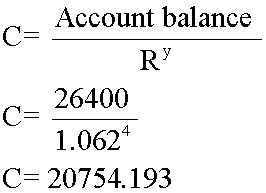 
£20,754.19
5 years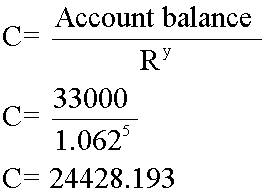 
£24,428.19
5. Interpret the solution
It appears that a monthly repayment of £550 would service a loan from just under £3,000 to just under £25,000.
6. Compare with reality
The results seem very low. This basic model assumed interest was compounded yearly and has not taken repayments into account.
Second go around
2. Set up a model
Create an Excel spreadsheet that uses the PV function to calculate the present value of a loan or an investment, based on a constant monthly interest rate.
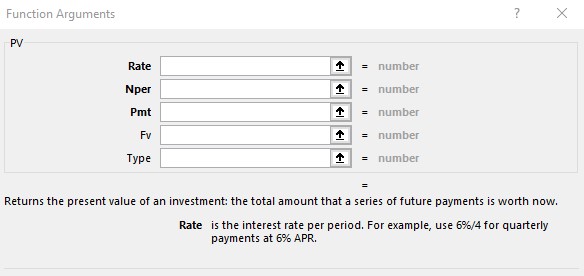
This requires the following variables :
- Rate The monthly effective interest rate per year.
- Nper The total number of payment periods.
- Pmt The fixed payment made each period .
3. Formulate the mathematical problem
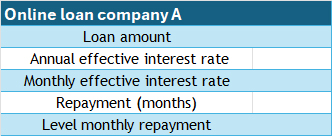
To do this, create a little table in Excel with cells for
- Loan amount
- Annual effective interest rate
- Monthly effective interest rate
- Repayment (months)
- Level monthly repayment
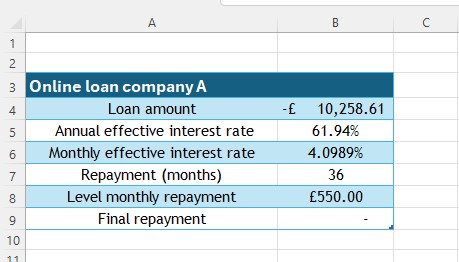
Like this :
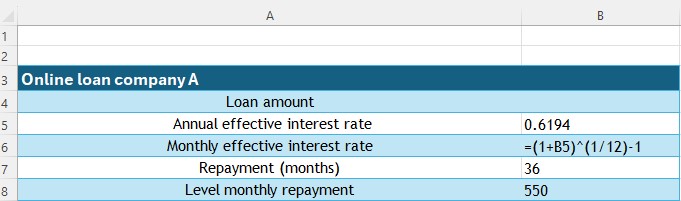
The monthly effective rate of interest can be calculated in Excel using the formula
=(1+cell with annual rate)^(1/12)-1
This takes the annual rate, adds 1 then takes the twelth root of the result. 1 is then subtracted from the result.
In the diagram below, the formula is
=(1+B5)^(1/12)-1
To calculate the loan amount, insert the PV function , found in the Financial section of Formulae
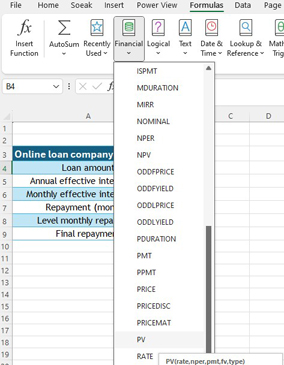
The following screen appears:
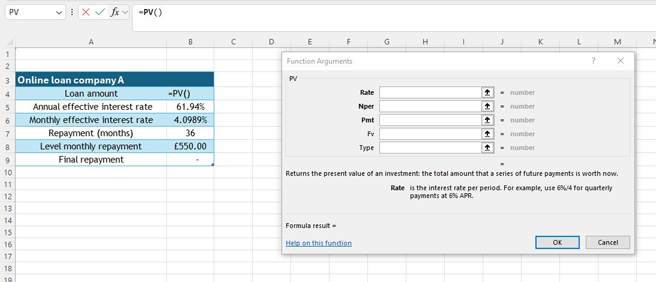
Enter the variables
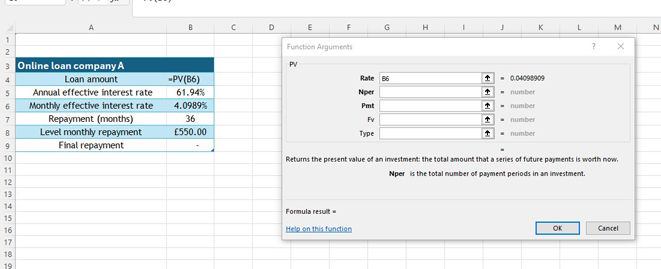
Rate is monthly effective rate , here cell B6
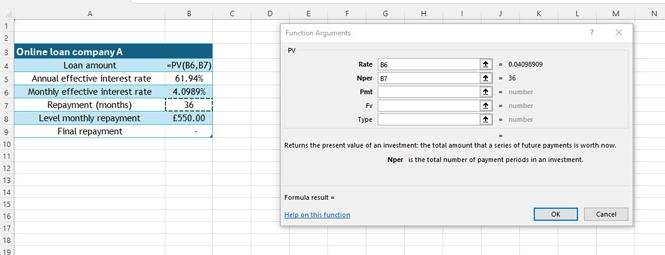
Nper is the number of repayments, here cell B7
Pmt is the fixed monthly repayment , here cell B8
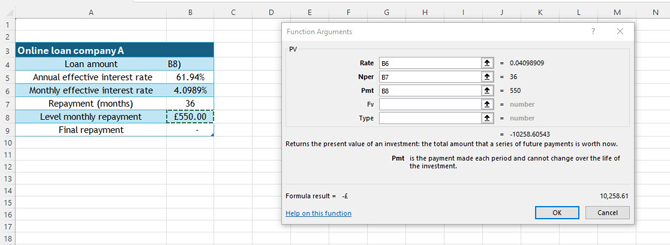
The amount of the loan is shown as a negative number.
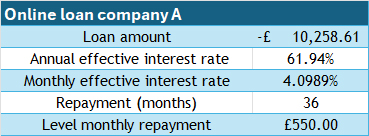
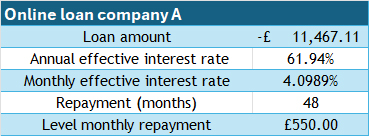
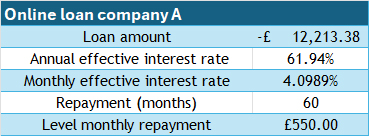
4. Solve the mathematical problem
Online loan company A , interest rate 61.94% per year
Online loan company B , interest rate 19.9% per year
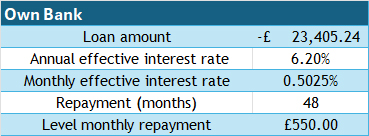
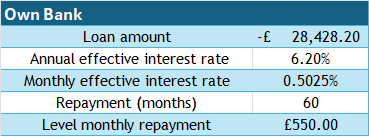
Own Bank, interest rate 6.2% per year
5. Interpret the solution
If the loan is taken over 3 years, approximately £18,000 can be borrowed.
If the loan is taken over 4 years, approximately £23,000 can be borrowed.
If the loan is taken over 5 years, approximately £28,000 can be borrowed.
Price range is £18,000 to £28,000
Loan rates depend on the credit score for the individual.
The cost of the loan varies considerably :
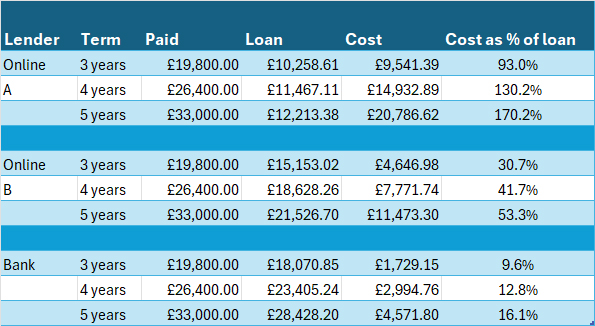
Banks tend to offer much better interest rates than online finance companies.
6. Compare with reality
A quick comparison of the model with an online quote :
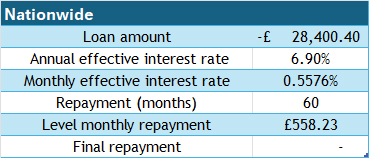
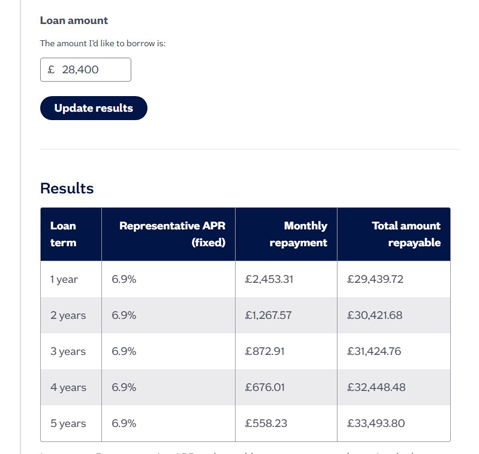
The model is quite realistic.
Fermi Problems
Named after Nobel prize winner Enrico Fermi , Fermi problems often require reasonable assumptions and estimates to be made about the situation to come up with an approximate answer. Multiple approaches and answers exist.
Example
How many toilet rolls are required per year for the population of the UK ?
Assumption 1 :Average person uses 1 roll per week.
Assumption 2 : UK Population 66.7 million
Assumption 3 : 85% of population usage.
Estimate : 1 x 52 x 66.7 million x 0.85 = 2, 948.14 million toilet rolls.
2,948,140,000
University of Maryland
Fermi Problems Site
© Alexander Forrest