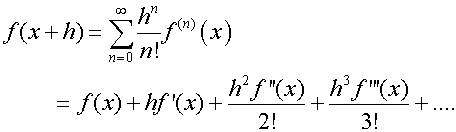Infinite Series

An infinite series has an infinite number of terms.
The sum of the first n terms, S_n , is called a partial sum.

If S_n tends to  a limit as n tends to infinity, the limit is called the sum to infinity of the series.

 

Arithmetic series

 

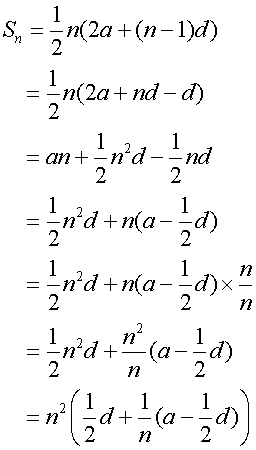
As n tends to infinity, S_n tends to
The sum to infinity for an arithmetic series is undefined.

 

Geometric series

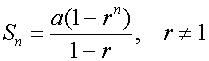
When r > 1,  r_n tends to infinity as n tends to infinity.
When r < 1,  r_n tends to zero as n tends to infinity.

 

The sum to infinity for a geometric series is undefined
when

The sum to infinity for a geometric series
when    
is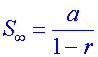       

Example

Find the sum to infinity  for the series

96 +48 +24…… if it exists.

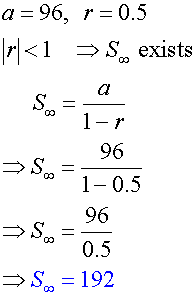
Example

Express the recurring decimal  0.242424…. as a vulgar fraction

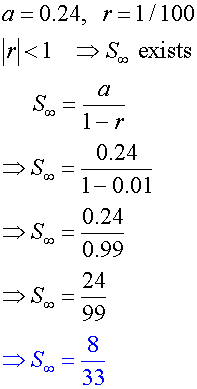
Example

Given that 12 and 6 are two adjacent terms of an infinite
geometric series with a sum to infinity of 192,

a) Find the first term.
b) Find the partial sum S6

 

Solution
a)

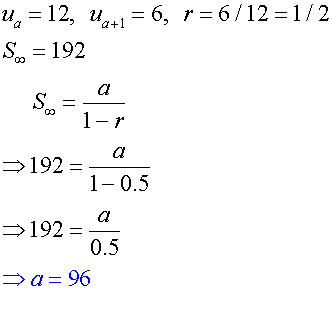
b)

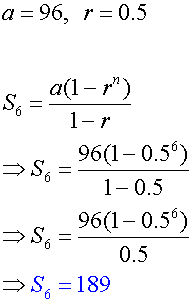
Sigma notation - Rules

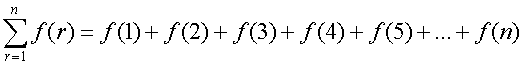
Constant multiplier

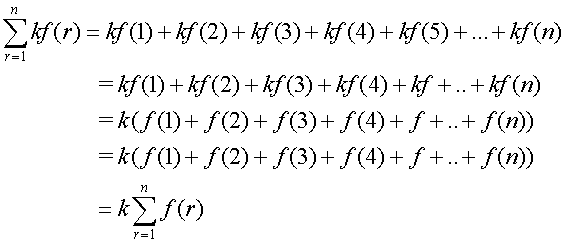
Adding series

 

Binomial theorem refresher

 

Sum of first n natural numbers

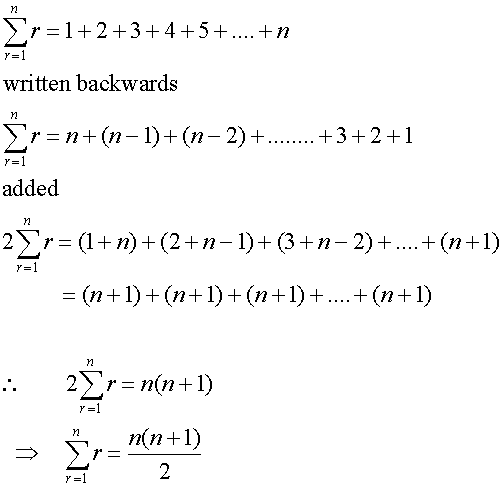
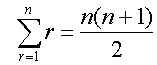
Useful result

 

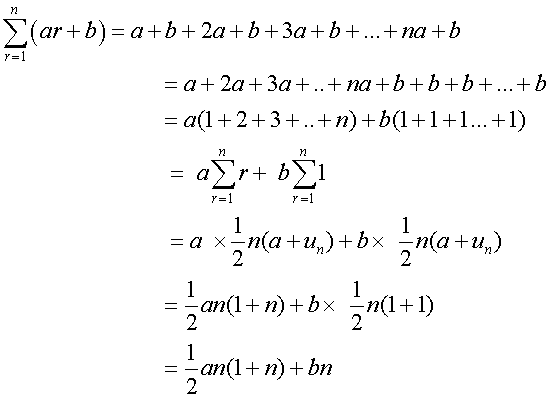
Example

Find the value of

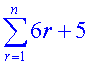
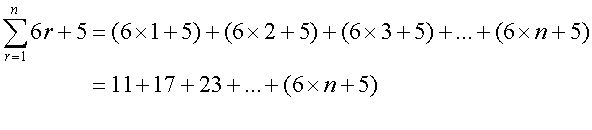
From the rules above,

 

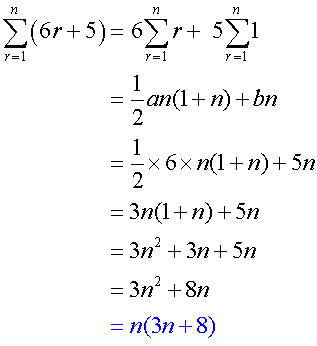
Common series  - Sigma notation

 

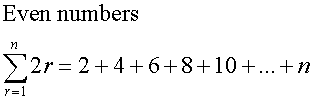
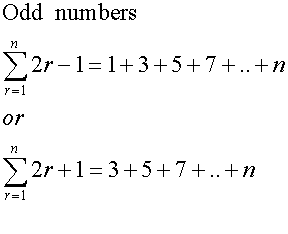
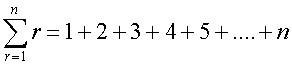
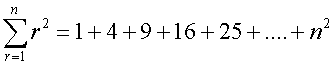
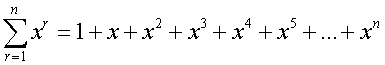
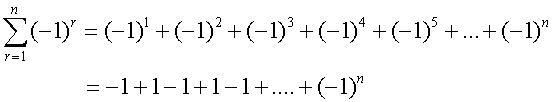
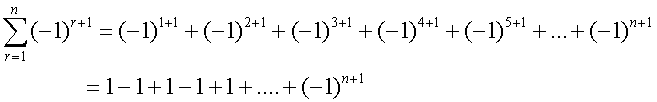
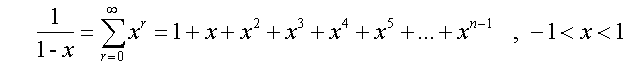
Power Series

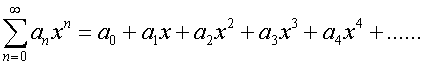
where a₀,a₁,a₂…a_n are constants.

The series always converges when x = 0
It will possibly converge for other values of x.

A series cannot be convergent unless its terms
tend to zero

 

D’Alembert’s ratio test

For a series of positive terms

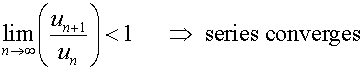
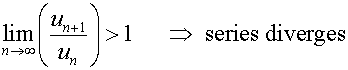
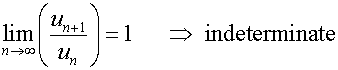
Example

Use d’Alembert’s ratio test to test for convergence
of the following series :-

 

 

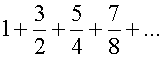
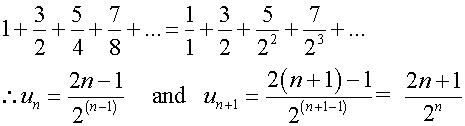
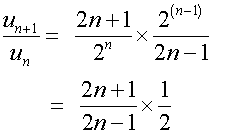
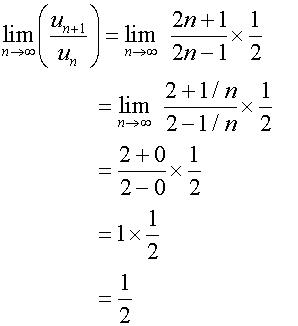
Absolute convergence

 

If

 

 

 

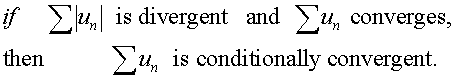
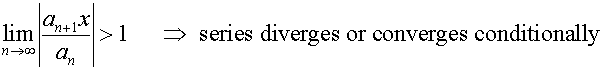
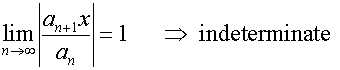
Example

Find the sum to infinity of the series

4 + 7x +10x²+13x³+…

and the region of valid values of x.

 

 

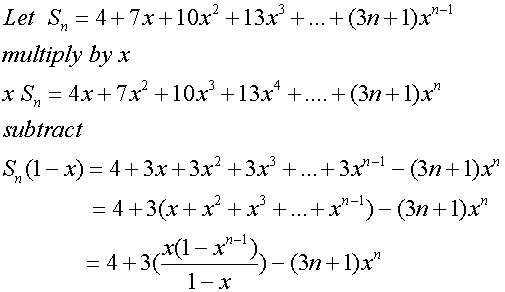
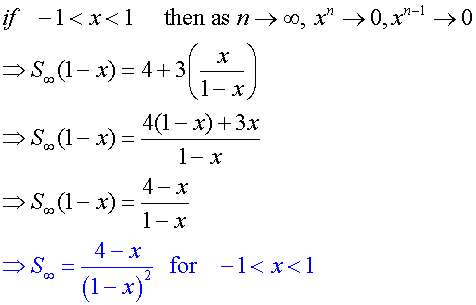
Fibonacci series

 

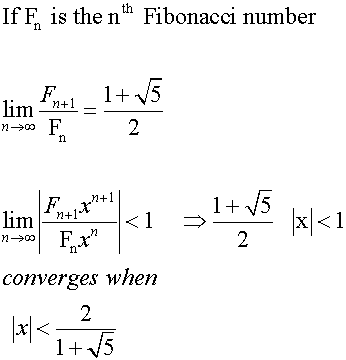
Centre of convergence

The power series can be written

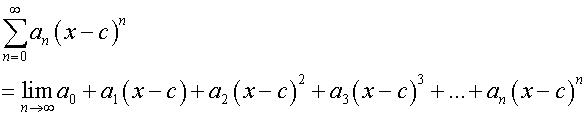
where c is the centre of convergence.
This is the middle of the interval of convergence,
the interval for which the limit exists.
The radius of convergence is called R.

If R = ∞ , the series converges for all x.
Otherwise,

the series converges for

and diverges for

 

To find a₀,  set x = c , since the remaining terms will
become zero.

differentiate

To find a₁, evaluate f’(c)

go again

 

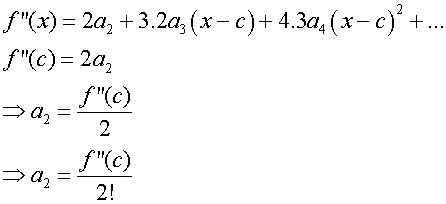
Continuing  gives the following

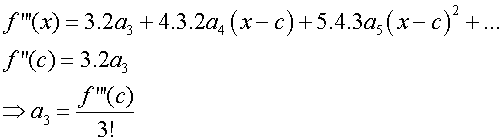
and

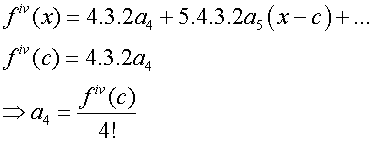
so that

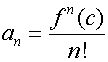
Substituting back into the original series

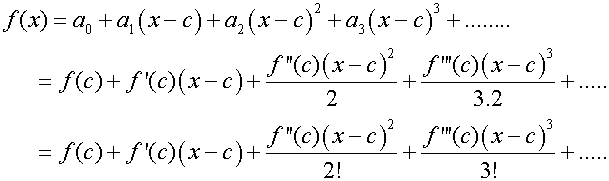
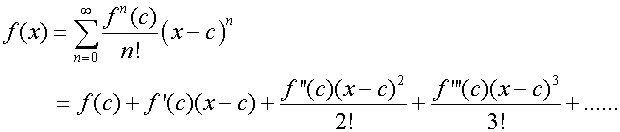
In the interval (-R+c,R+c)

 

Taylor’s series

 

Example