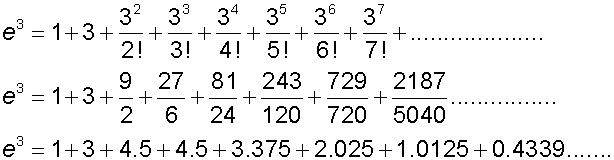Maths Mutt HOME


Factorials

Example

Fred knows that the code to his locker is made up of the digits 5,6, 7 and 8 , but he can’t remember the order. How many different  possible codes exist to open his locker ?

There are 4 ways of listing the first number,

5***           6***                   7***              8***

and 3 ways of listing the second number.

56**

65**

75**

85**

57**

67**

76**

86**

58**

68**

78**

87**

This leaves 2 ways of selecting the third number

567*

657*

756*

856*

568*

658*

758*

857*

576*

675*

765*

865*

578*

678*

768*

867*

586*

685*

785*

875*

587*

687*

786*

876*

Finally, this leaves only one way of selecting the last number.

5678      6578     7568       8567
5687      6587     7586       8576
5768      6758     7658        8657
5786      6785      7685       8675
5867      6857      7856       8756
5876     6875      7865        8765

 

There are 24 possible codes.

4x3x2x1=24
This is called  4-factorial and is written 4!

0! = 1  By definition
1! = 1
2! = 2X1=2
3! = 3X2X1 = 6
4! = 4X3X2X1=24
5! = 5X4X3X2X1 = 120

In general
n! = nx(n-1)x(n-2)x(n-3)………x3 x 2 x1

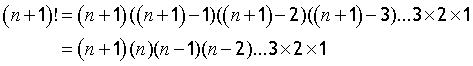
factorial

so

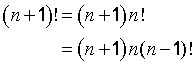
factorial (n+1)

Likewise

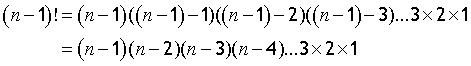
factorial n-1)

so

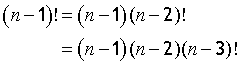
factorial (n-1)

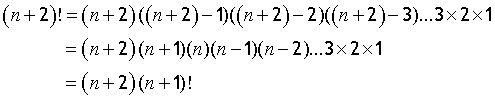
factorial(n+2)

 

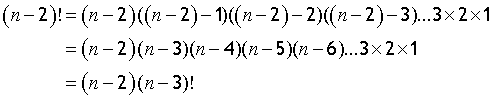
factorial(n-2)

Note,
5 x 4! = 5x 24 = 120 = 5!

 n x (n-1)! = n!     so    (n-r+1)x (n-r)! = (n-r+1)!     

Permutations and Combinations

A permutation is an ordered arrangement  of objects, in which order matters.

A group of n different objects has  n!  possible  permutations .

1

A combination is  an arrangement  of objects where order does not matter.

2

Example

There are 56 ways of choosing 5 different tins of catfood from  8 brands, but 6720 ways of ordering them!

7

6

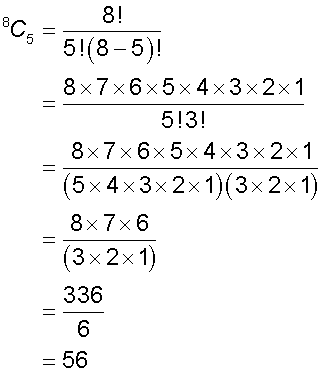
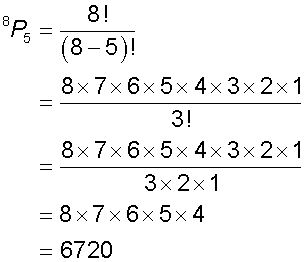
Properties of combinations

3 4

5

 

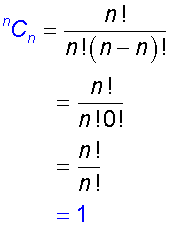
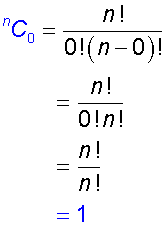
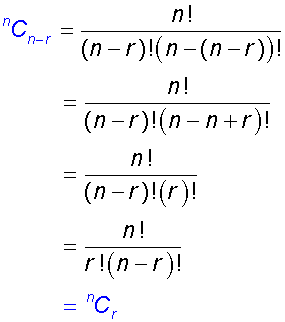
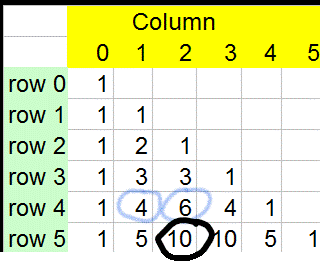
Pascal's triangle

 

3

The triangle is built by adding the row above.

 

 2

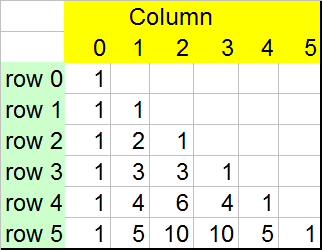
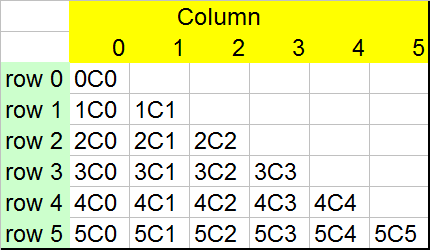
This can be written nCr   , where n is the row, r is the column

1

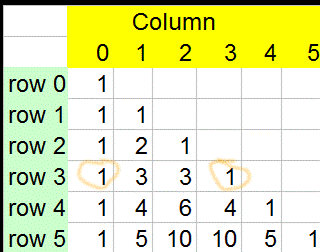
Notice how3C3=3C0 = 1 

row26

 

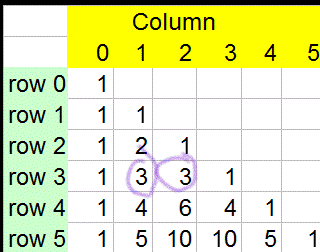
and 3C2=3C1 = 3 

row27

 

and 4C3=4C1= 4 

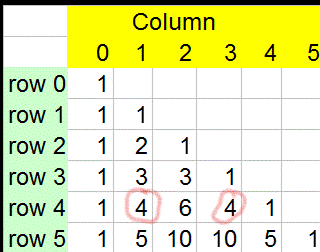
row28

 

Also, notice

8

add2

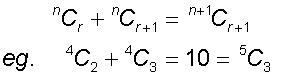
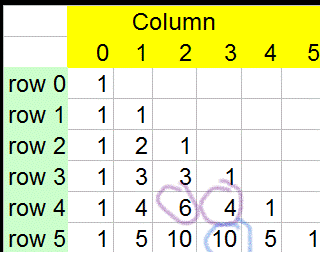
and

9

 

add

 

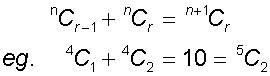
Binomial coefficients

 

The coefficients are known as binomial coefficients.

nCr can be written in the form 10

where n is the row and r is the column in pascal's triangle

rc

So for the example given above

row23

ncr

 

 rc2

 

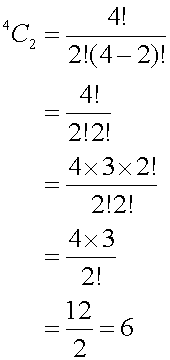
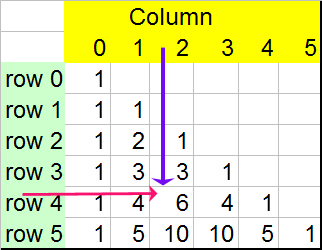
Notice that

 

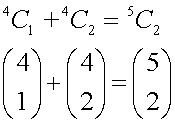
row24

 

Properties to learn

11

 

12

 

13

 

14

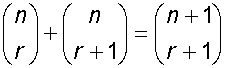
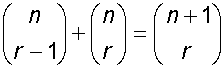
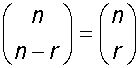
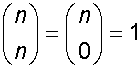
Example

Show that

exa

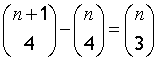
where n ≥ 4

Start by writing out the left-hand side in the form

ncr :

 

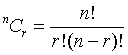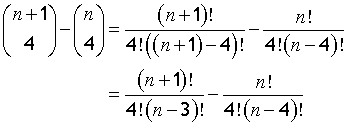
question

multiplyingthe second term by 1 in the form of (n-3)/(n-3) gives

show

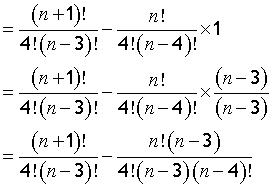
which reduces to

shio

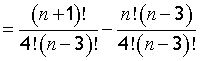
since (n-3)!= (n-3)(n-4)!

Now the denominators are the same

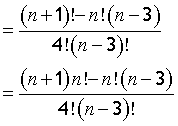
show5

take out common factor n!

6

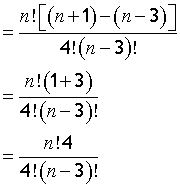
finally,

last

 

 

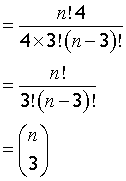
Equations

Example

Solve the equation

17

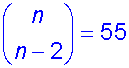
From the properties above, since

13

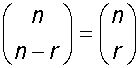
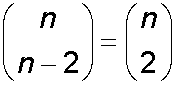
row30

 

Solution

18

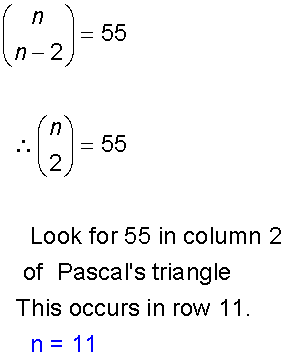
Alternatively,

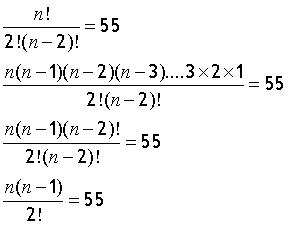
eqn12

tidy up

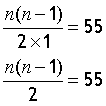
eqn13

make equation and solve

14

 

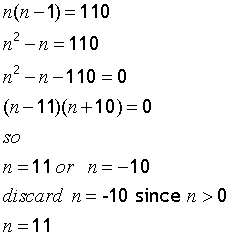
Example

Solve the equation

12

19

 

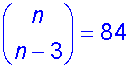
Binomial expansions

Example

20

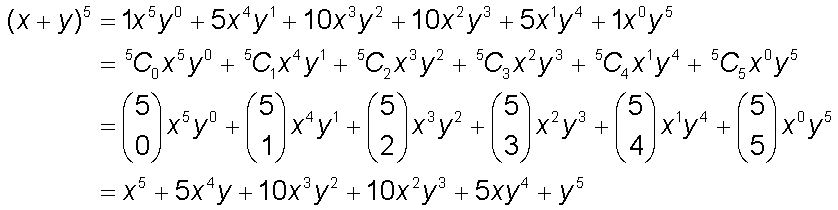
Notice that the powers of x and y both add up to 5, and that as the powers of x decrease from 5 to 0, the powers of y increase from 0 to 5.

In General

21

23

25

24

 

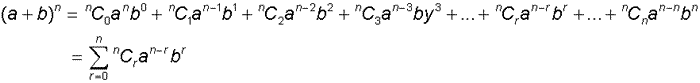
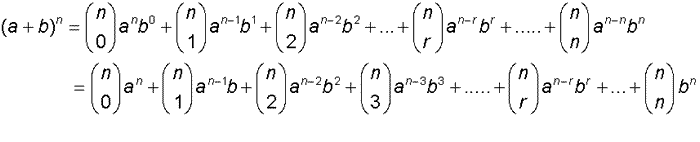
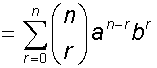
This is known as the binomial theorem, and gives the expansion of (a + b)n , where a and b are real numbers and n is a natural number.

The binomial coefficients are found in the nth row of Pascal’s triangle.

35

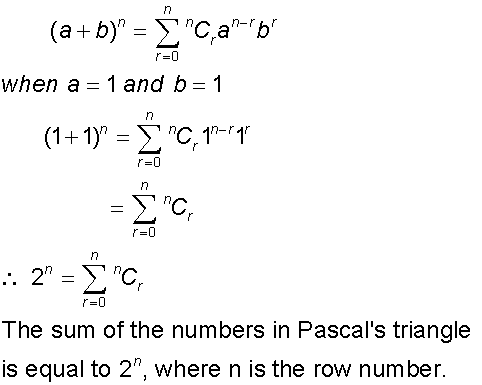
Examples

Expand the following:
     

26

       

27

 

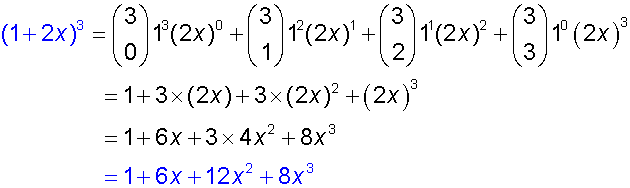
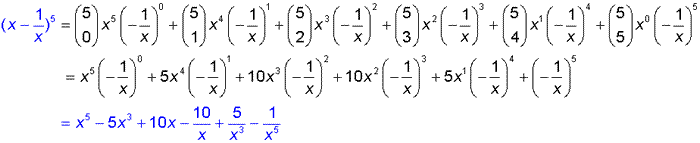
The binomial theorem allows a specific term to be found from the  general form.


28      

     29

30

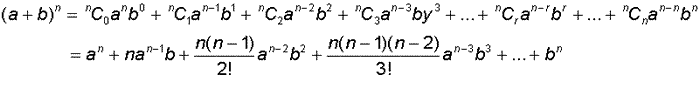
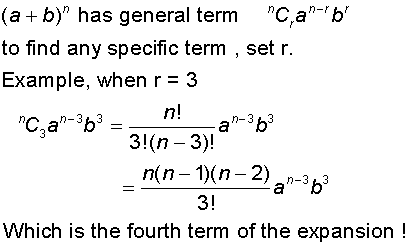
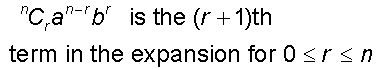
Example
Find the seventh term in the expansion of (2x +3y)9

31

     

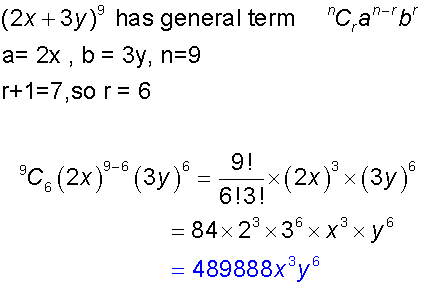
Find the term containing x3 in the expansion of (3 +2x)5

32

          

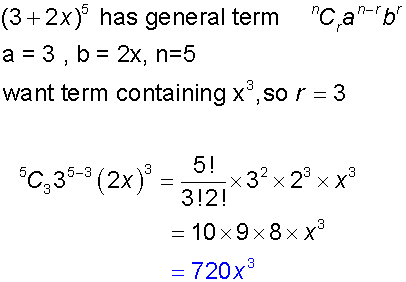
Probability and the binomial theorem

   

33

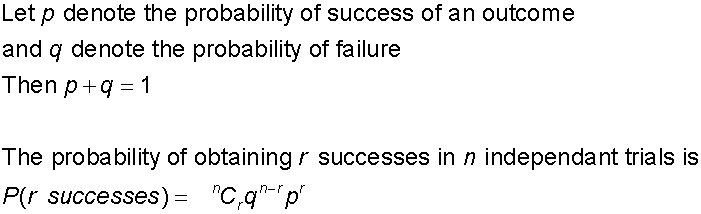
Example

34

 

The binomial expansion and e

 36

37

38

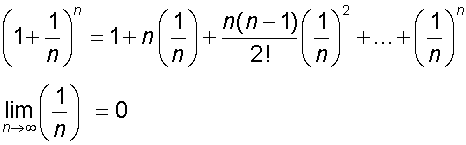
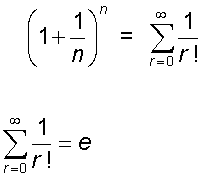
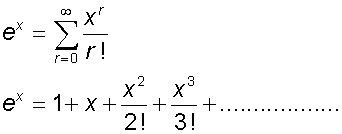
Examples

39

© Alexander Forrest