Differential Equations

These equations, containing a derivative, involve rates of change – so often appear in an engineering or scientific context.
Solving the equation involves integration.

 

The order of a differential equation is given   by the  highest derivative used.

The degree of a differential equation is given  by the  degree of the  power of the highest derivative used.

Examples

   

Types of differential equations :-

• First order Differential Equations
• First order Linear  Differential Equations
• Second order  Linear Differential Equations
• Second order non – homogeneous Differential Equations
• Examples of Differential Equations

 

 

First order Differential Equations

Solving by direct integration

The general solution of differential equations of the form
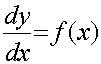 can be found using direct integration.
Substituting the values of the initial conditions will give

Example

Solve the equation

 

 

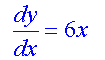
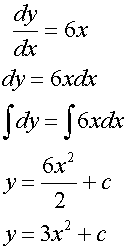
Example

 Find the particular solution of the
differential equation

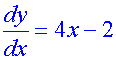
   given  y = 5 when x = 3

 

 

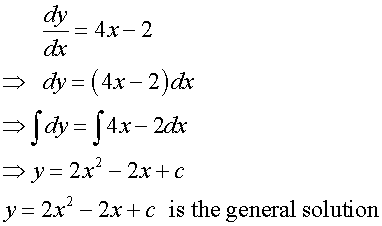
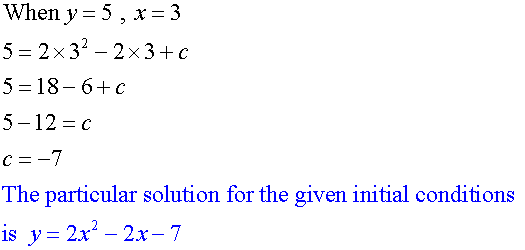
Example

 A straight line with gradient 2 passes through
the point  (1,3). Find the equation of the line.

  

 

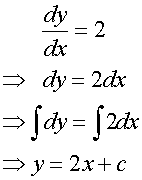
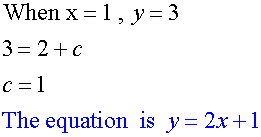
Variables Separable

A variables separable differential equation is one
in which the equation can be written with all the terms
for one variable on one side of the equation, and the other
terms on the other side.

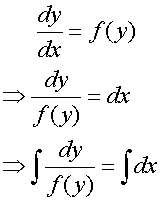
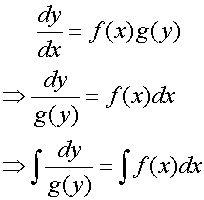
Example

  Find the general solution of the differential equation

           

  

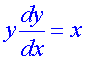
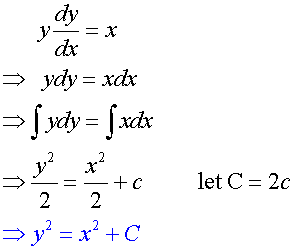
Example

 Find the general solution of the differential equation

      

 

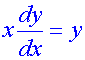
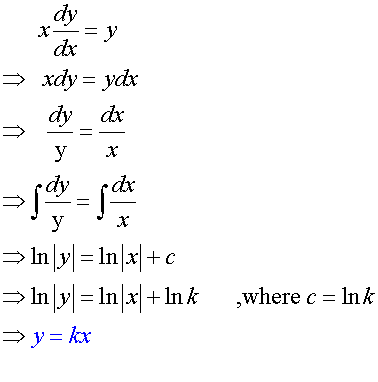
Example

 Find the particular solution of the differential equation

     

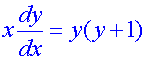
  given y = 2 when x = 1

  

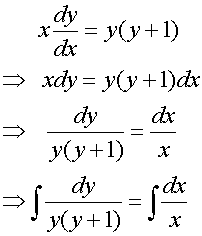
Partial fractions are required to break the left hand side of the equation into a form which can be integrated.

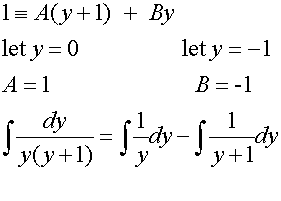
so

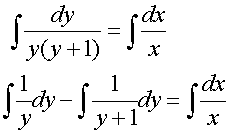
which integrates to general solution

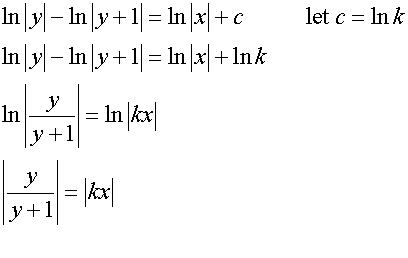
substitute values for particular solution

 

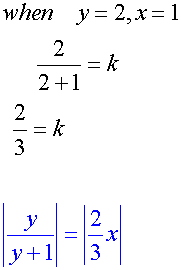
Linear  Differential Equations

 These are first degree differential equations.

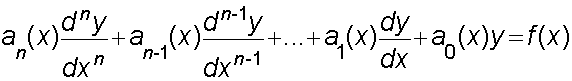
   describes a  general linear differential equation  of order n,
where a_n(x), a_n-1(x),etc and f(x) are given functions of x or constants.

Louis Arbogast introduced the differential operator
D = d/dx  , which simplifies the general equation to

 

or

 

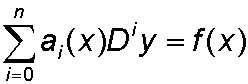
If f(x) = 0 , the equation  is called homogeneous.
If f(x) ≠0 , the equation is non-homogeneous

 

First order Linear  Differential Equations

To solve equations of the form

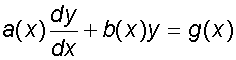
1) Express in standard form

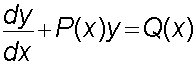
where  P and Q are functions of x or constants

2) Multiply both sides by the Integrating Factor

3) Write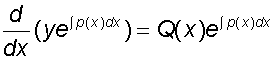 

 

4) Integrate the right hand side,

use integration by parts if necessary

 

5) Divide both sides by the integrating factor.
This gives the General solution.

6) Use any initial conditions to find
particular solutions.

 

Example

Find a general solution of the equation

    

    

  

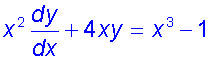
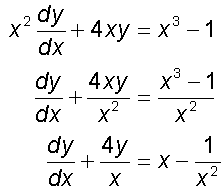
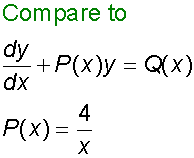
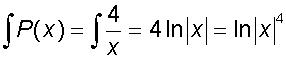
so

 

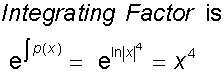
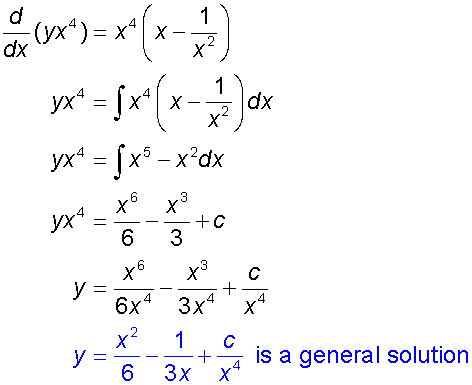
Example

Find a general solution of the equation

 

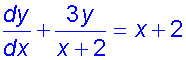
   where x ≠2 , and hence find the particular solution
for y = 1 when x=-1

 

 

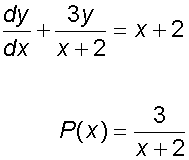
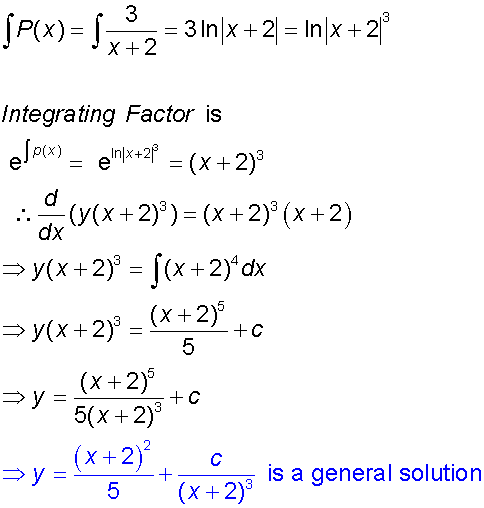
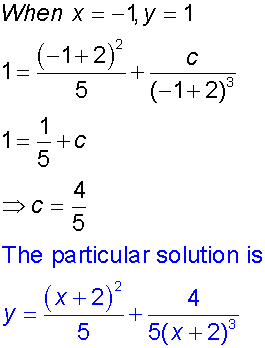
Second order  Linear Differential Equations

To solve equations of the form

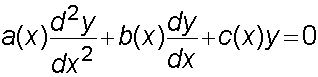
1) Write down the auxiliary equation
am² +bm + c = 0         

2) Examine the discriminant of the auxiliary equation.

3) For real and distinct roots,  m₁ and m₂,

the general solution is

4) For real and equal roots,
the general solution is

 

5)For complex conjugate roots,
   m₁= p + iq  and m₂ = p - iq  ,
the general solution is

6) Use any initial conditions to find the particular solution.

 

Example

 Find the general solution of the equation

 

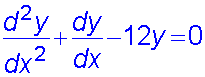
  and the particular solution for which
y = 7 when x=0 and dy/dx = 7

  

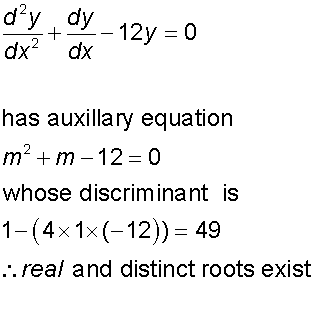
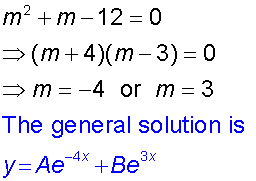
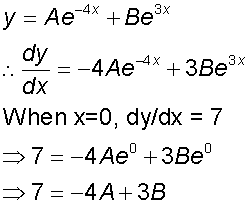
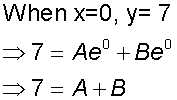
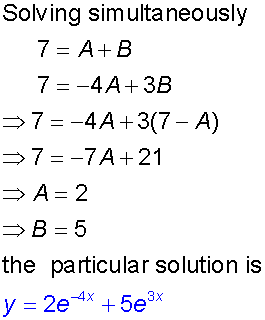
Example

  Find the general solution of the equation

  

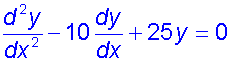
  and the particular solution for
y=0 and dy/dx = 3 when x=0

   

    

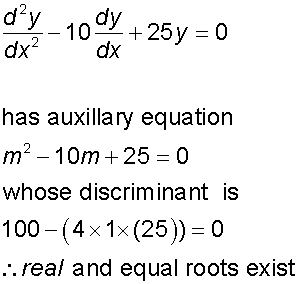
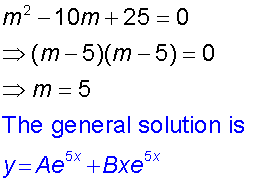
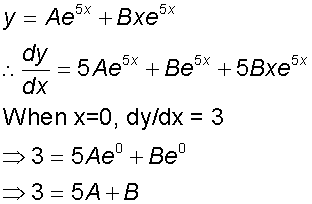
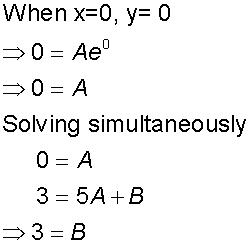
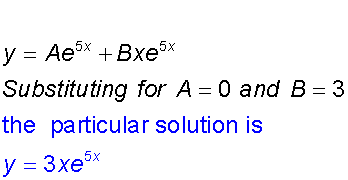
Example

 Find the general solution of the equation

 

   

 

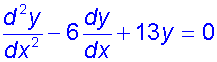
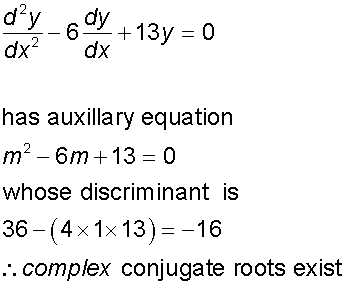
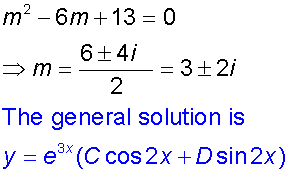
Second order non – homogeneous Differential Equations

      The solution to equations of the form

     

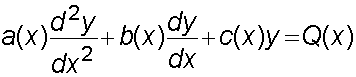
          has two parts, the complementary function (CF)
and the particular integral (PI).

so Q(x) = CF +PI

The CF is the general solution as described above
for solving homogeneous equations .

 The Particular Integral is found by substituting
a form similar to Q(x) into the left hand side equation,
and equating co-efficients.

• If Q(x) is a linear function, try y = Cx +D
• If Q(x) is quadratic, try Cx² +Dx +E
• If Q(x) is wave function, try CSinx +Dcosx
• If Q(x) is a constant, try y = C
• If Q(x) is e^kx, try y = Ce^kx

The PI cannot have the same form as any of the terms in the CF,
so care has to be taken to ensure that this is not the case.
In such a situation, an extra x term is usually introduced to the PI.

  A particular solution is found by substituting initial conditions into the general solution. Do not just use the CF!!!

Example

Find the general solution of the equation

    

 

     

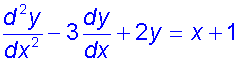
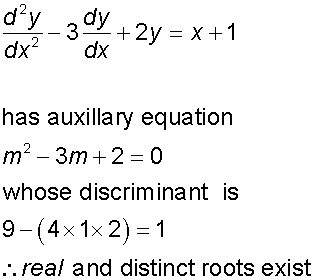
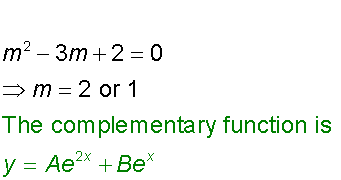
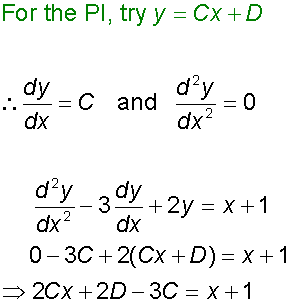
Example

  Find the general solution of the equation

    

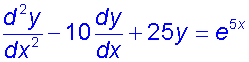
  and the particular solution for
y=0 and dy/dx = 5 when x=0

 

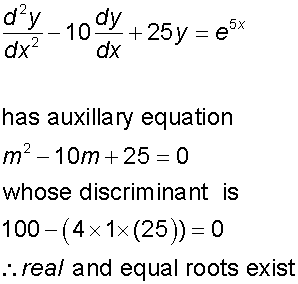
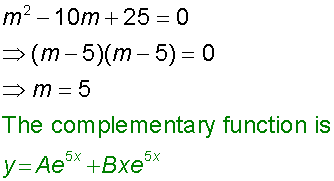
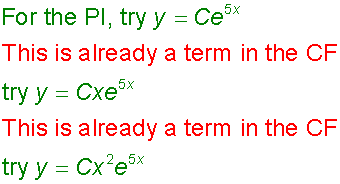
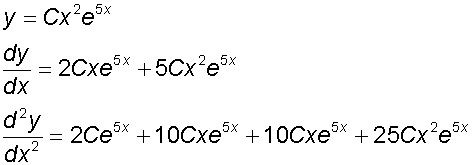
Now, substitute these back into the original equation

 

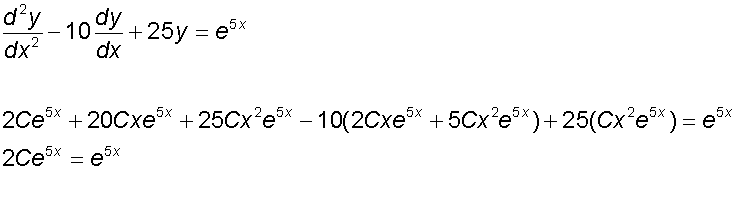
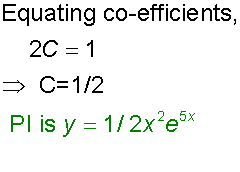
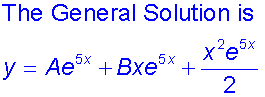
Now find the particular solution

 

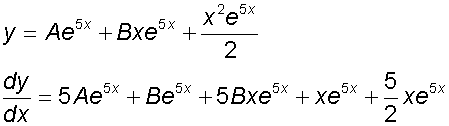
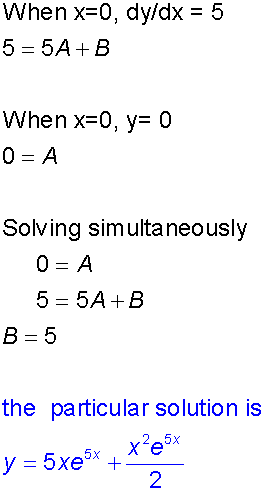
Phew!!