Differentiation

Differential Calculus concerns the rate of change of a function  with respect to the change in the variable on which it depends.

For example,

Speed is  a measure of distance travelled by an object in a unit period of  time.
The distance travelled totally depends on the time taken.

Instantaneous speed is the speed of an object at a particular time.
Average speed = total distance divided by total time taken.

Velocity is  a measure of the distance travelled by an object in a particular direction over  a unit period of  time.
Acceleration is  a measure of how the velocity of an object changes with time.

The derivative of a function for some particular value is a measure of the rate at which the function is changing at that particular value.

The derivative of a function for some particular value
is also the gradient of the graph of the function at that point.

The gradient of a straight line is found by dividing the change
in the y-axis ( the y-step) by the change in the x-axis ( the x-step).

But what happens if we need to find the gradient of a curve ?

 

The points A(2,4) and B(3,9) lie on the  curve y = x² .

 

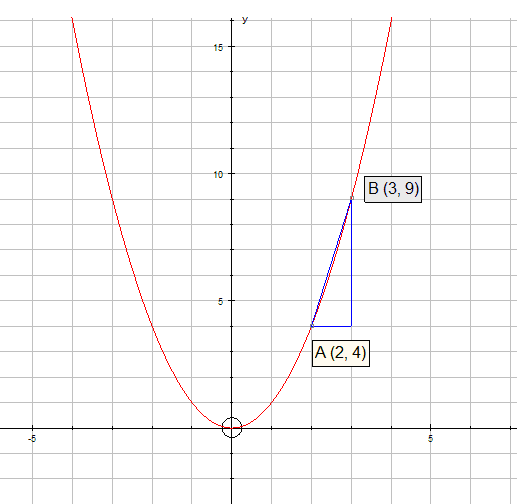
  The average gradient of the curve from A to B is the gradient of the chord AB.

 

   

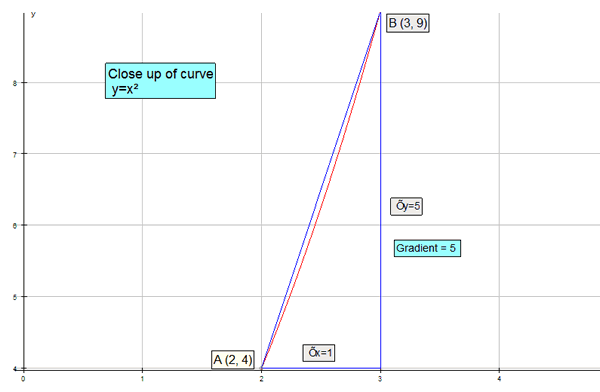
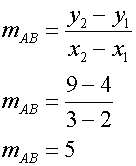
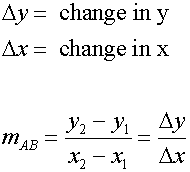
As B moves towards A, the  gradient of the curve changes.

 

                                         

 

  
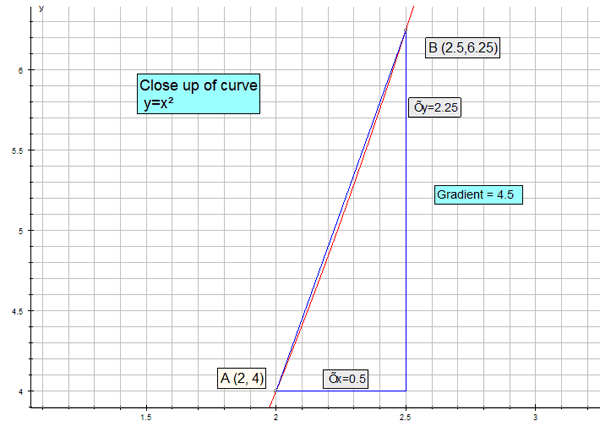
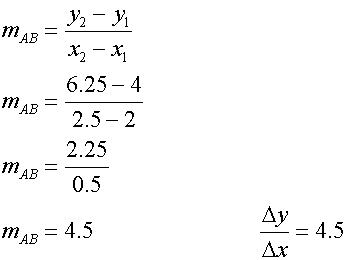
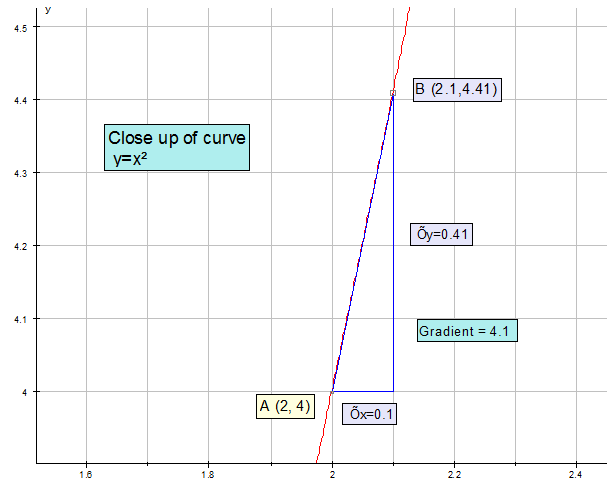
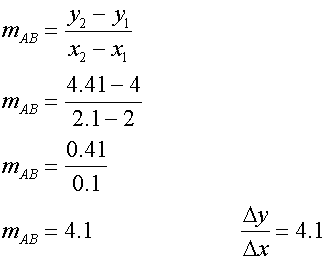
The closer B is to A,the nearer it reaches a limit.

 

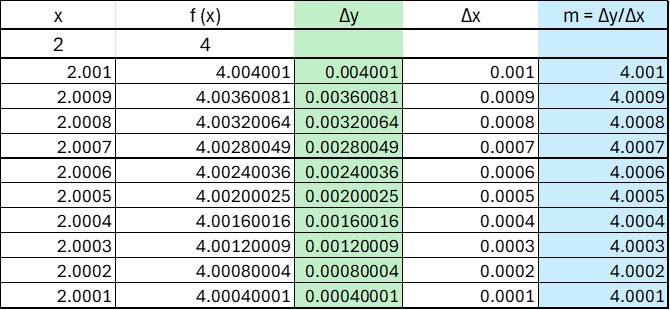
This limit is the gradient of the curve and occurs at the tangent to the curve at the point A.

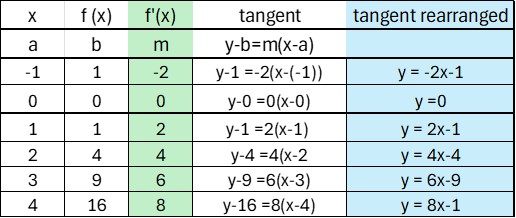
When A is the point ( 2, 4), the gradient of the curve is 4.

   
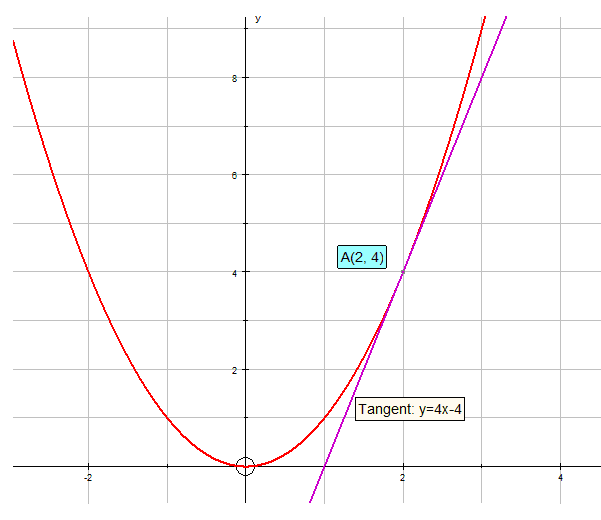
Other points have different gradients.

 

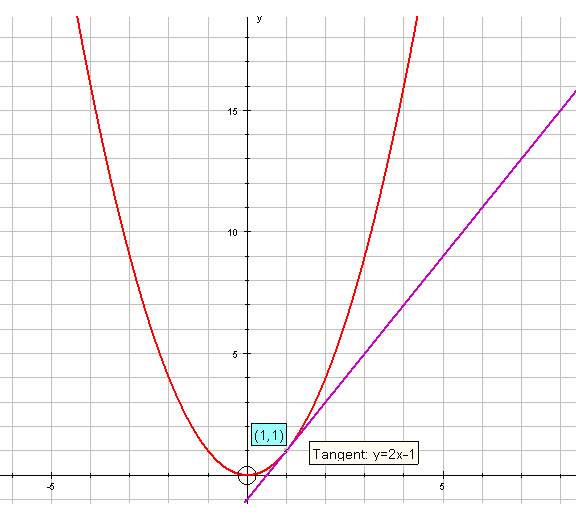
  Is there an easier way to find the gradient of the curve at other points ?

 First Principles

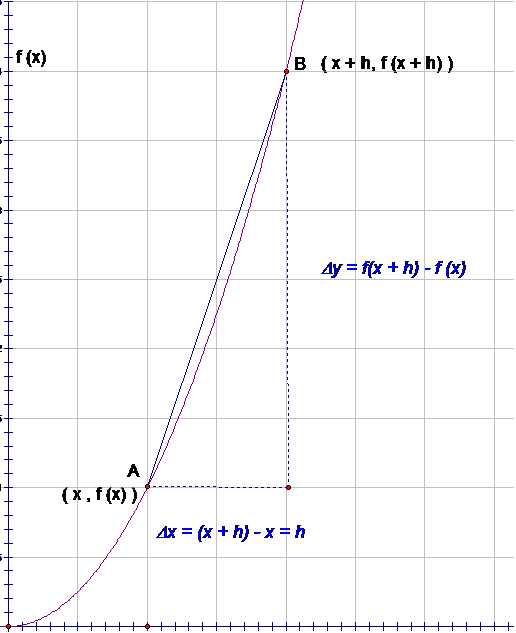
  Let  A(x, f(x))  and B(x+h,(f(x+h)) be  points on the graph y = f(x)

      

 

 

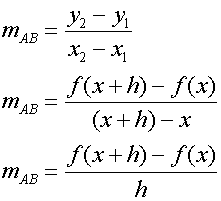
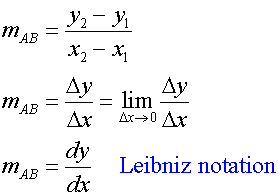
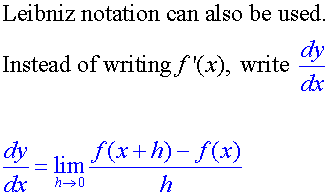
Deriving f’(x) from f(x)

   using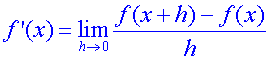 

 

Example

   If f(x) = x² , find f’ (x)

    

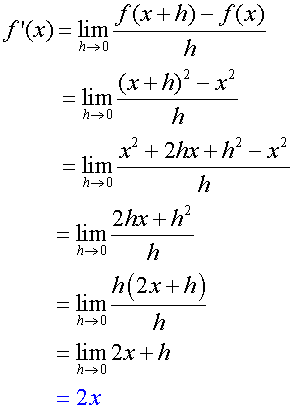
The derived function of x is f’(x) = 2x
The derivative  when x = 3 is 6

This means that the rate of change of the function is 2x, and that the gradient of the tangent to the graph of the curve y = x² at any point is found by doubling the x co-ordinate.

The gradient of the tangent to the graph at the point (3, 9) is 6.
The gradient of the tangent to the graph at the point (4, 16) is 8.

The equation of the tangent can be found by using y - b = m(x-a)

In General

If f(x) = xⁿ then f’(x) = nx^n-1        (n is a rational number)

Example

   If f(x) = x³ , find f’ (x)

 

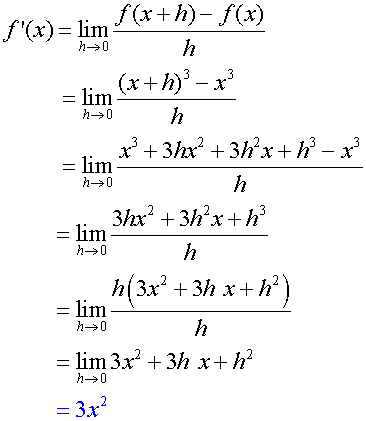
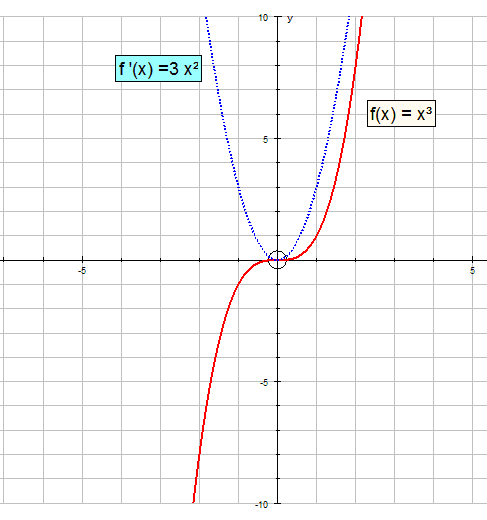
More examples