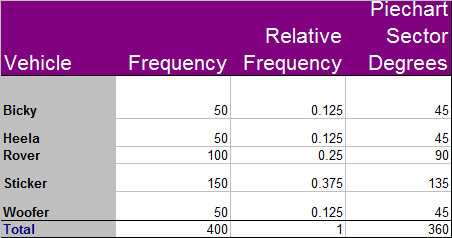
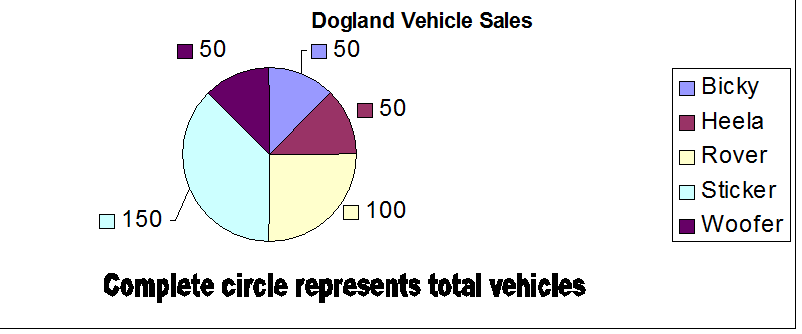
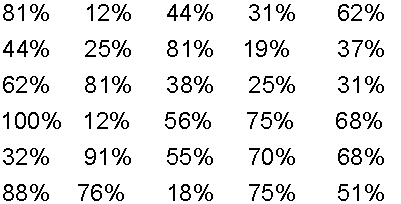Calculated Statistics

Mean

The mean is the sum of the data divided by the number of bits of data.

This is also known as the arithmetical average.

\[ \text{Mean} \;=\; \frac{\text{Sum of all of the data}} {\text{Total number of bits of data}} \]

It is represented like this:

\[ \bar{X} = \frac{\sum X}{n} \]

\[ \bar{X} \text{ is called x bar and represents the mean} \] \[ \sum X \text{ is the sum of the data} \] \[ n \text{ is the number of bits of data (batch size)} \]

Example

Find the mean of the list:

2, 4, 6, 8, 12

\[ \text{Mean} = \frac{2 + 4 + 6 + 8 + 12}{5} \] \[ = \frac{32}{5} \] \[ = 6\frac{2}{5} \]

The formula can be re-arranged:

\[ \bar{X} = \frac{\sum X}{n} \]

\[ \bar{X}\, n \;=\; \sum X \]

\[ n \;=\; \frac{\displaystyle \sum X}{\bar{X}} \]

Example

Find the sum of the list of 8 numbers which has a mean of 18.

Sum = mean × n

= 18 × 8

= 144

Median

The middle value of an ordered batch of data is called the median.

Median = middle value of an ordered list.

If there are an odd number of bits of data, the median will be the value at \( \frac{1}{2}(n+1) \), where n is the batch size.

If there are an even number of bits of data, the median will be exactly halfway between the two values at \( \frac{1}{2}n \).

Example

Find the median of the list:

2, 6, 12, 8, 4

Here, n = 5

This is odd, so calculate \( \frac{1}{2}(n+1) \)

\( \frac{1}{2}(5+1) = 3 \)

The median is the third number in the ordered list.

This can be seen if the data is laid out like so:

Example

6, 8, 10, 2, 12, 4

Here, n = 6

This is even, so calculate \( \frac{1}{2}n \)

\( \frac{1}{2} \times 6 = 3 \)

The median will be halfway between the 3rd and 4th numbers in the ordered list.

\[ \text{Median} = 2,\;4,\;6\;\uparrow\;8,\;10,\;12 \] \[ \text{Median is halfway between } 6 \text{ and } 8 \] \[ \text{Median} = \frac{6 + 8}{2} \] \[ \text{Median} = \frac{14}{2} \] \[ \text{Median} = 7 \]

This can be seen if the data is laid out like so:

Mode

The mode is the most recurring number in a list. Not all lists have a mode.

The Mode =The most occurring number.

Example

\[ \text{Find the Mode of the list:} \] \[ 2,\;4,\;6,\;8,\;12,\;12,\;15,\;4,\;2,\;6,\;8,\;7,\;7,\;9,\;12 \] \[ \text{Mode} = 12 \]

Example

\[ \text{Find the Mode of the list:} \] \[ 2,\;8,\;6,\;4,\;10,\;12,\;2,\;4,\;8,\;8,\;4 \] \[ \text{Mode} = 4 \text{ and } 8 \]

Range

The range is the difference between the highest and lowest numbers.

\[ \text{Range} = \text{Highest - Lowest} \]

Mid Range

The mid range is halfway between the highest and lowest values.

\[ \text{MidRange} = \frac{1}{2}\,( \text{Highest} + \text{Lowest} ) \]

Example

The list 2.5,4,33,6,7,9,8
Highest (H) = 33 , Lowest (L) = 2
\[ \text{Range} = 33 - 2 = 31 \]

\[ \text{MidRange} = \frac{1}{2}\,(\text{Highest} + \text{Lowest}) \] \[ = \frac{1}{2}\,(33 + 2) \] \[ = \frac{1}{2}\times 35 \] \[ = 17.5 \]

The five-figure summary

The highest Number H ( also known as E_U)
The lowest Number L ( also known as E_L)
The median, the number which halves the list Q2 ( also known as M)
The upper quartile, the median of the upper half Q3 ( also known as Q_U)
The lower quartile, the median of the lower half Q1 ( also known as Q_L)

Example

2 4 5 5 6 7 7 8 8 9 10

jkk

n = 11

This is odd, so calculate 1/2( n+1)

1/2( n+1) = 1/2( 11+1) = 1/2 x 12 = 6

The median is the 6th position, so Q2 = 7

There will be (n-1) /2 numbers in each half.
So there will be 5 numbers in each half.
The lower quartile is the median of the lower half, so Q1 = 5
The upper quartile is the median of the upper half, so Q3 = 8

or

bloy

5 -fig summary
H = 10
L = 2
Q1 = 5
Q2 = 7
Q3 = 8

This information can be represented as a box plot :-

Spread

When comparing distributions, it is useful to know:

The central trend (mean, mode or median)
The spread (use range, interquartile range or semi‑interquartile range)

The spread in statistics — representing the variability or dispersion of a set of data values — measures how far the data points are from the centre or the average of the distribution. The further the spread, the less consistent the result.

The interquartile range is the range between the upper and lower quartiles.

Interquartile range = \( Q_3 - Q_1 \)

The Semi‑Interquartile Range (SIQR) is half of the interquartile range.

Semi‑Interquartile Range = \( \tfrac{1}{2}(Q_3 - Q_1) \)

Example

Compare the two sets of maths results.

Paper 2 has a better score overall, since more than three quarters of the candidates got a score of 50 or more, whereas only 50% of those sitting Paper 1 got between 50 and 80%.

Paper 2 has a larger spread of marks and a median of 70%, but both papers have the same interquartile range.

Skewness

If the shape of the diagram is almost the same when a horizontal line is drawn across it, then the batch is symmetric.

The left-hand part is equal to the right-hand part,
or \(E_U - M = M - E_L\).

Otherwise, it is skew.

If the smaller values are further apart than the larger values, the batch is left-skew (the data bulges near the bottom).

If the smaller values are closer together than the larger values, the batch is right-skew (the data bulges near the top).

The left-hand part is longer than the right-hand part,
or \(E_U - M < M - E_L\).

The right-hand part is longer than the left-hand part,
or \(E_U - M > M - E_L\).

Measure of Skewness based on Quartiles

\(Q_U\) = Upper Quartile (Q3)

\(Q_L\) = Lower Quartile (Q1)

\[ \frac{Q_U + Q_L - 2M}{dQ} \] \[ \frac{Q_U + Q_L - 2M}{\,Q_U - Q_L\,} \]

or

\[ \frac{Q_3 + Q_1 - 2Q_2}{\,Q_3 - Q_1\,} \]

If the result is positive, the data is right‑skewed.
If the result is negative, the data is left‑skewed.

Example

A 5‑figure summary of data gives:

\[ \frac{Q_U + Q_L - 2M}{\,Q_U - Q_L\,} \] \[ = \frac{77.5 + 48.5 - (2 \times 68)}{77.5 - 48.5} \] \[ = \frac{126 - 136}{29} \] \[ = \frac{-10}{29} \]

The value is negative, so the data is left‑skewed.

Standard Deviation

This is a measure of how much the data varies from the mean.

\[ s = \sqrt{\text{variance}} \]

Variance is the mean of the squares minus the square of the mean.

\[ \text{Variance} = \frac{\sum x^{2}}{n} \;-\; \left( \frac{\sum x}{n} \right)^{2} \]

A standard deviation of zero indicates that the data and the mean are effectively the same.

Two formulae are given by the SQA to calculate the standard deviation:

\[ s = \sqrt{ \frac{ \sum (x - \bar{x})^{2} }{ n - 1 } } \] and \[ s = \sqrt{ \frac{ \sum x^{2} \;-\; \frac{(\sum x)^{2}}{n} }{ n - 1 } } \]

Using the first equation

Find the mean by adding the data and dividing by n
Find the difference between the data and the mean (x̄)
Square these differences
Add up the total of the squared differences
Plug into the first equation given in the test paper

Using the second equation

Square the data to get \( x^2 \)
Find totals \( \Sigma x \) and \( \Sigma x^2 \)
Square the total \( \Sigma x \) and divide by n
Plug into the second equation given in the test paper

Example

Calculate the standard deviation of the numbers:
101, 105, 133, 142, 185, 186

First Equation

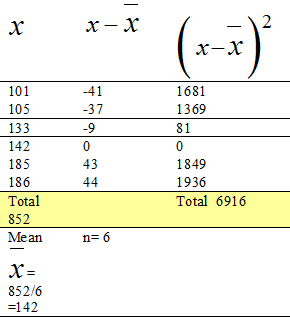
Find the mean
Find the differences from the mean
Square the differences
Add the squared differences
Substitute into the formula

\[ s = \sqrt{ \frac{ \sum (x - \bar{x})^{2} }{ n - 1 } } \] \[ = \sqrt{ \frac{ 6916 }{ 6 - 1 } } \] \[ = \sqrt{ \frac{6916}{5} } \] \[ = 37.1914 \]

Using equation 2

Square the data
Find totals \( \Sigma x \) and \( \Sigma x^2 \)
Square \( \Sigma x \) and divide by n
Substitute into the formula

\[ s = \sqrt{ \frac{ \sum x^{2} \;-\; \frac{(\sum x)^{2}}{n} }{ n - 1 } } \] \[ s = \sqrt{ \frac{ \color{red}{127900} \;-\; \frac{\color{blue}{852}^{2}}{6} }{ 6 - 1 } } \] \[ s = \sqrt{ \frac{ 127900 \;-\; \frac{725904}{6} }{ 5 } } \] \[ s = \sqrt{ \frac{ 127900 - 120984 }{ 5 } } \] \[ s = \sqrt{ \frac{6916}{5} } \] \[ s = \sqrt{1383.2} \] \[ s = 37.1914 \]

Changing all of the numbers by the same amount does not affect the standard deviation.

Example

The standard deviation of:

101, 105, 133, 142, 185, 186

is the same as the standard deviation of:

1, 5, 33, 42, 85, 86

and

4, 8, 36, 45, 88, 89

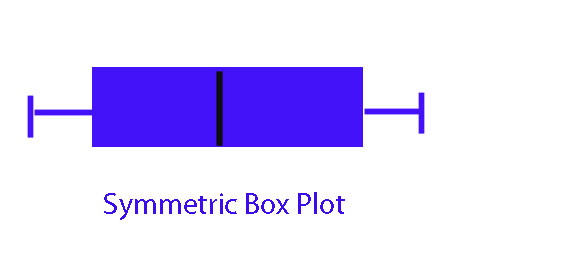
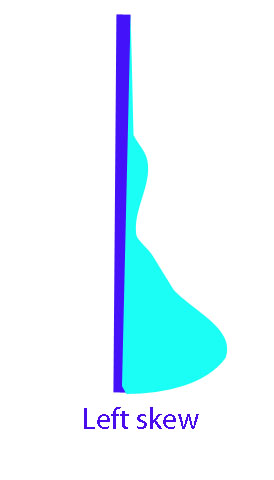
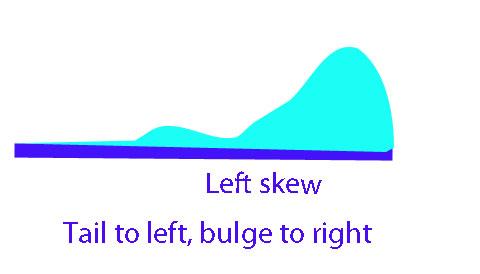
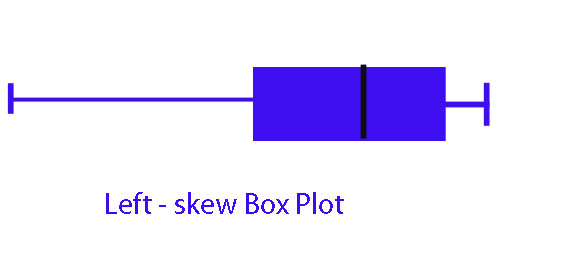
Interactive - Standard Deviation

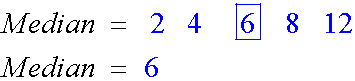
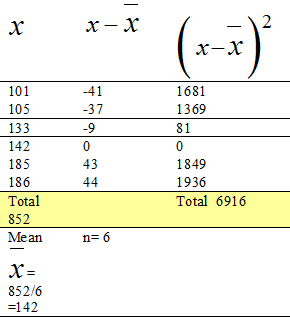
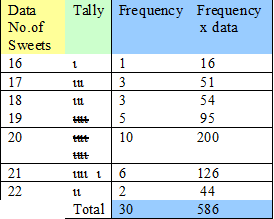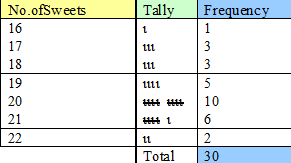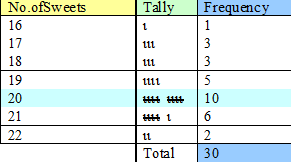
Frequency Tables

These are a useful way of collating raw data, to quickly see the mode, find the median, and calculate the mean.

Example

A manufacturer claims that each packet of Shazbo contains 20 sweets on average.

When 30 packets of Shazbo are examined, the results are as follows:

No. of sweets per packet:

18 17 22 19 20 20 21 19 18 20

21 19 21 19 20 20 20 17 19 21

22 18 17 16 20 20 20 21 21 20

Is the manufacturer correct?

Construct a frequency table of the data.

The table shows that the mode of the sample is 20 sweets, which has a frequency of 10.

The median value lies halfway between the 15^th and 16^th values.

The frequency column shows that the first 12 values have between 16 and 19 sweets. The 15^th and 16^th values have 20 sweets.

The median is therefore 20 sweets.

To calculate the mean, we need to add another column and multiply the frequency by the number of sweets.

\[ \text{mean} = \frac{\text{total number of sweets}}{\text{number of packets}} \] \[ = \frac{586}{30} \] \[ = 19 \frac{16}{30} \] \[ = 19 \frac{8}{15} \] \[ = 19.533333 \]

The mean is 19½ sweets, which could be rounded to 20 sweets.

The manufacturer is correct!