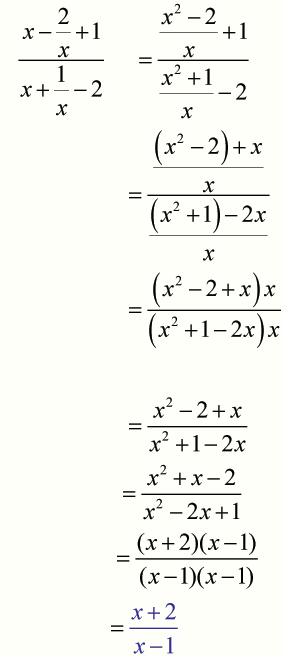Algebraic fractions

Example

Simplify

 

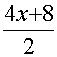
The task here is to find a way to breakdown the fraction, so that it can be divided by a common factor.

 

Here, a common factor of 4 exists

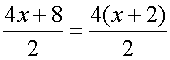
top and bottom are now divided by 2

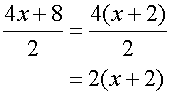
leaving 2(x +2) as the answer.

 

Likewise,

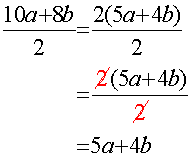
Sometimes, a line must be factorised first, using a difference of two squares if necessary:

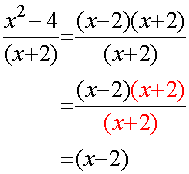
or

 

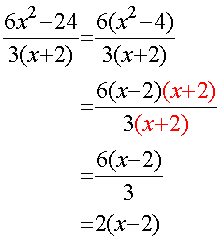
Solving equations with algebraic fractions

Example

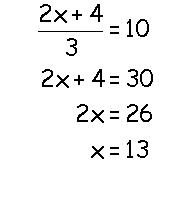
Get rid of the bottom numbers (denominators) by multiplying through on both sides:

 

 

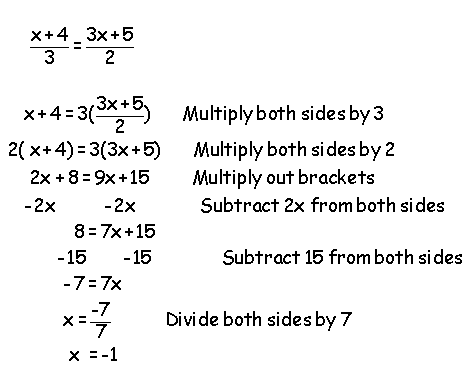
Operations on algebraic fractions

Use the normal rules for fractions.

To add or subtract fractions, the denominators must be the same.

Examples

Simplify

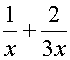
Normal way,

 

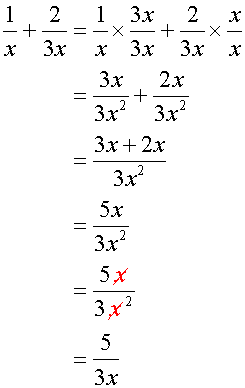
Vedic way,

Multiply bottom numbers (denominators), cross multiply and add:

 

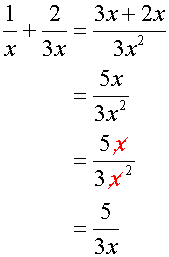
Example

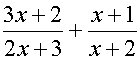
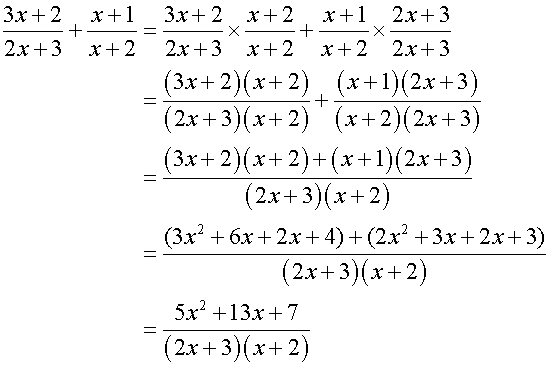
again, same question but done the vedic way :

 

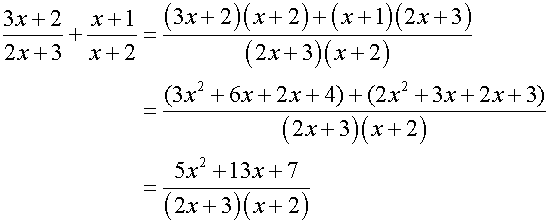
In Action

Remember that to multiply fractions, just multiply the tops( numerators) and then multiply the bottoms (denominators).

Don't forget to simplify if possible.

Example

Simplify

 

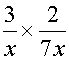
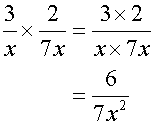
Another example,

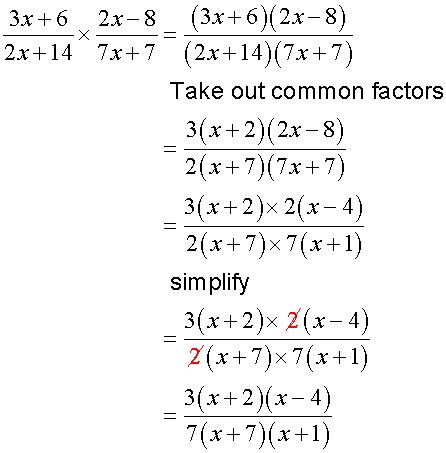
When dividing frations, remember to turn the second fraction upside down and turn the sum into a multipication.

 

Examples

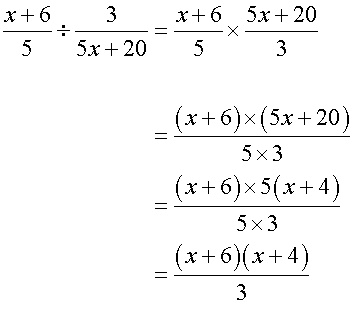
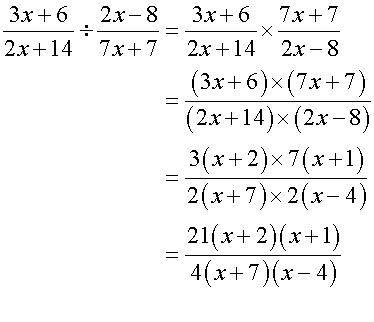
Or the alternative way:

 

 

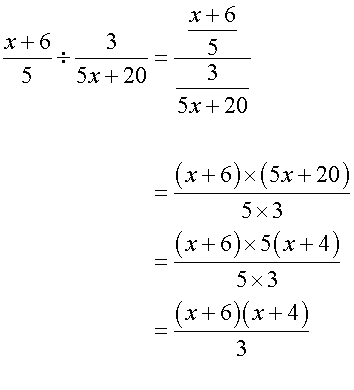
Complex fractions such as

 
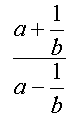
     can be  simplified using the multiplicative identity

       

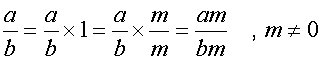
• Multiply the numerator and denominator of the fraction by the LCM.

         

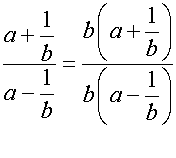
• Then expand brackets, factorise and simplify as usual.

         

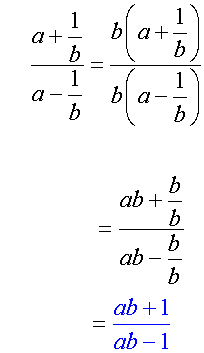
Examples

      1.  
           

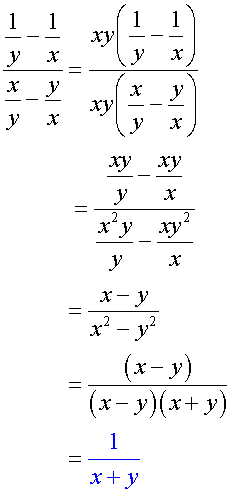
    2.
           

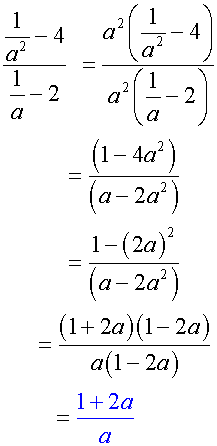
  3.

 

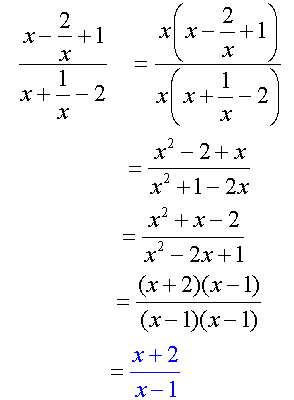
Alternatively, by using a combination of
vedic fraction addition and the alternative
method of fraction division :

1.

 

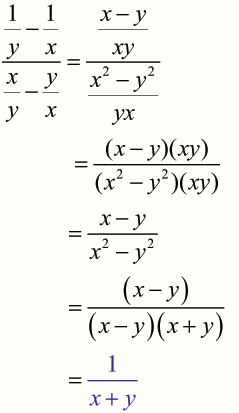
  2.      
                     

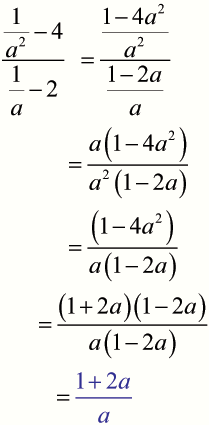
3.