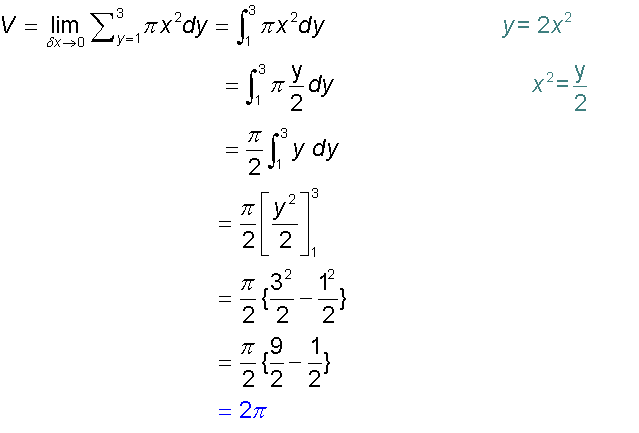Volumes of Solid of  Revolution

 

 

If a curve is rotated about an axis which it

does not cut, the area between the curve and

the axis will generate a  solid of revolution.

 

 

 

 

 

 

 

 

 

 

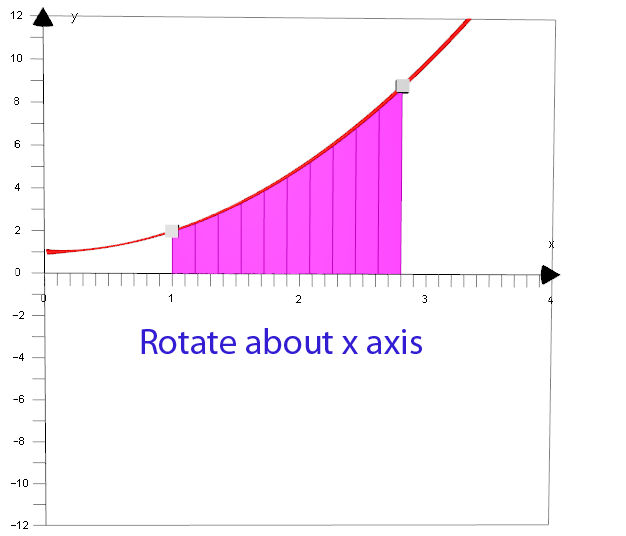
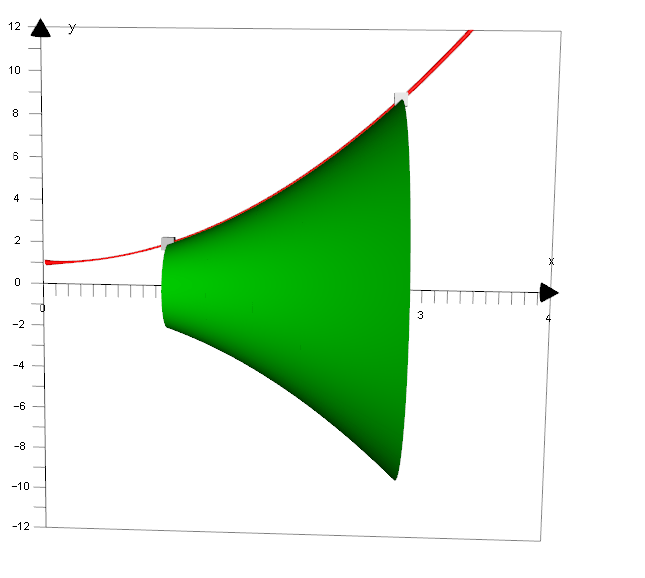
The volume generated is the limit of the sums

of the volumes of cylinders formed by

rotating rectangles.

 

 

 

If rectangle dx.y is rotated, a cylinder is formed

with height dy and radius y.

 

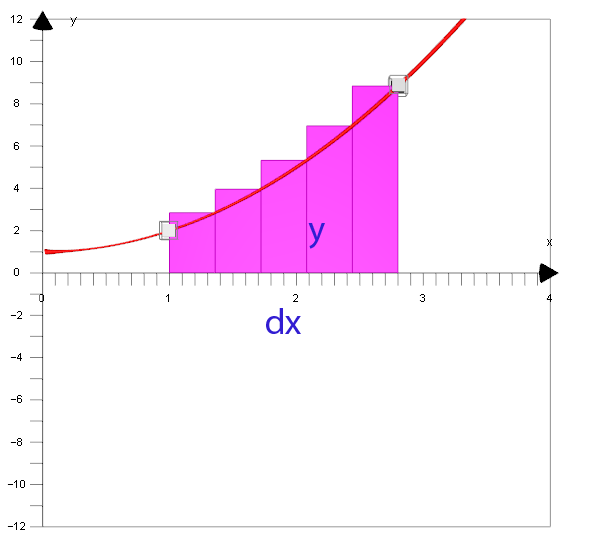
The volume of this cylinder is 

 

The volume of the solid of revolution is

 

 

 

 

Example

 

Find the volume and name the shape generated

by the rotation through 360˚ of the  positive branch

of the circle with equation  x²+y²=a²  about the x-axis.

 

 

 

 

 

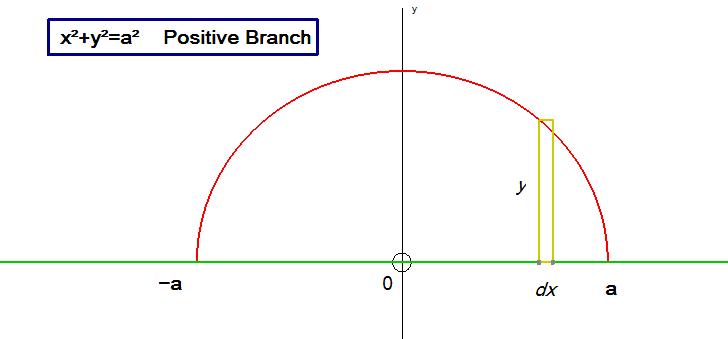
Volume

 

 

 

 

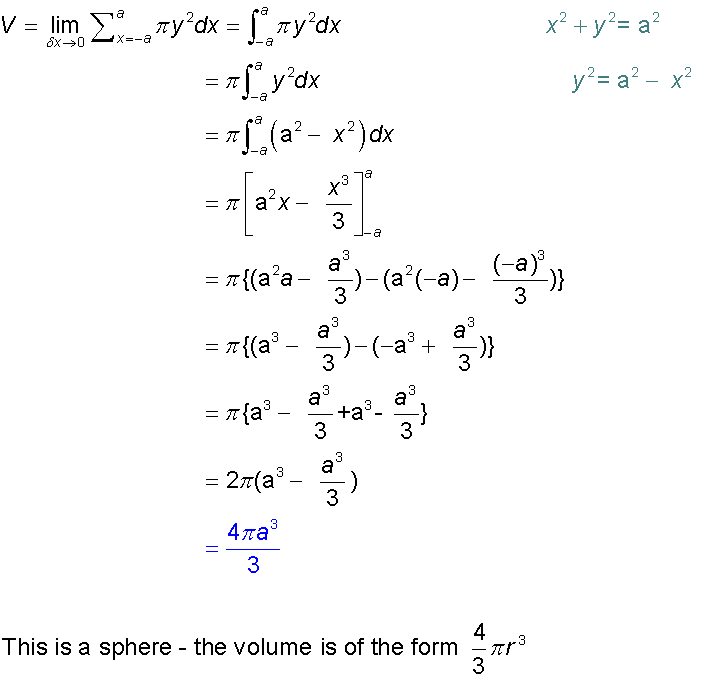
Example

 

The portion of the curve y=2x² between y=1 and y=3

is rotated  through 360˚  about the y-axis.

Find the volume of the resulting solid.

 

 

 

 

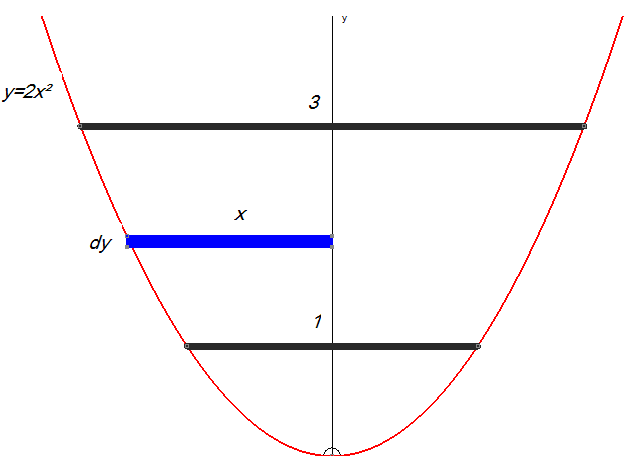
Volume