Vector Equations
The angle between two planes

The angle between two planes is found
using the scalar product.
It is equal to the acute angle determined by
the normal vectors of the planes.
Example
Calculate the angle between the planes
π1: x +2y -2z = 5
and π2: 6x -3y +2z = 8
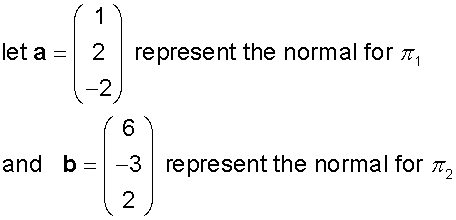
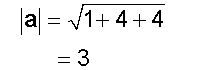
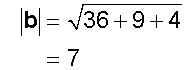
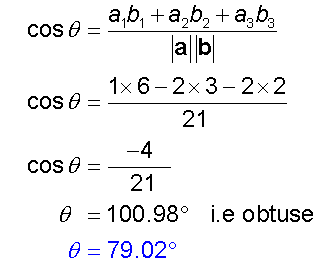
The distance between parallel planes
Let P be a point on plane π1 : ax + by + cz = n
a.x = n
and Q be a point on plane π2 : ax + by + cz = m
a.x = m
Since the planes are parallel, they share the common normal, a
a=(ai +bj+ck)
The distance between the planes is
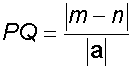
Example
Calculate the distance between the planes
π1: x + 2y - 2z = 5
and π2: 6x + 12y - 12z = 8
![]()
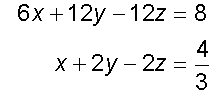
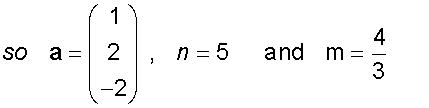
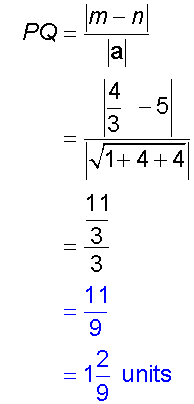
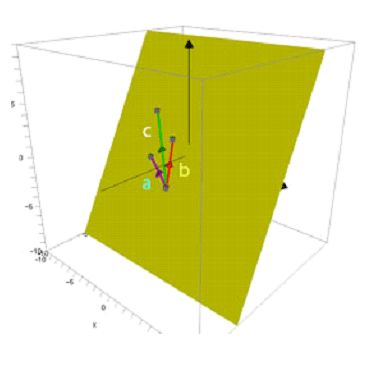
Coplanar vectors
If a relationship exists between the vectors a, b and c
such that c=λa+μb, where λ and μ are constants,
then vectors a, b and c are co-planar.
If three vectors are co-planar,
c=λa+μb
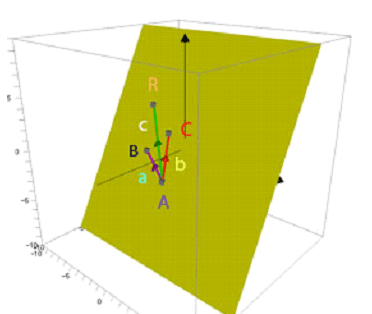
Vector equation of a plane
From the coplanar section above,
c=λa+μb
When position vectors are used,
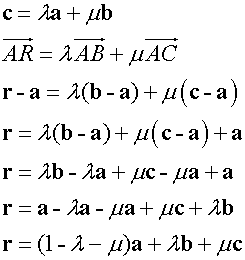
r=(1-λ-u)a+ λb+μc is the vector equation of the plane.
Since λ and b are variable, there will be many possible equations for the plane.
Example
Find a vector equation of the plane through the points
A (-1,-2,-3) , B(-2,0,1) and C (-4,-1,-1)
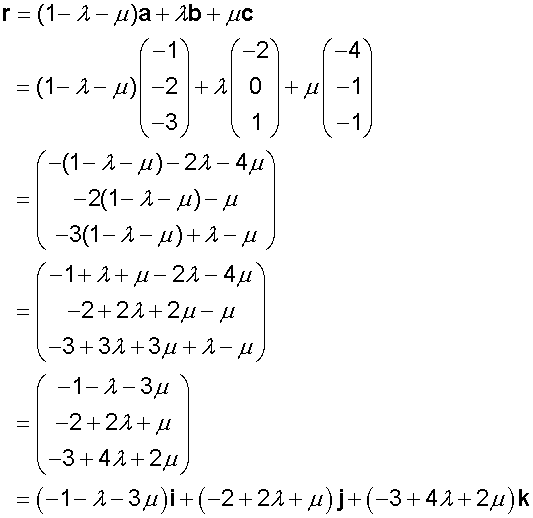
If λ = 2 and μ =3
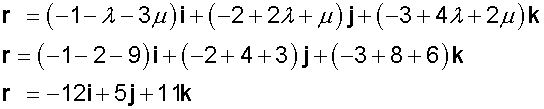
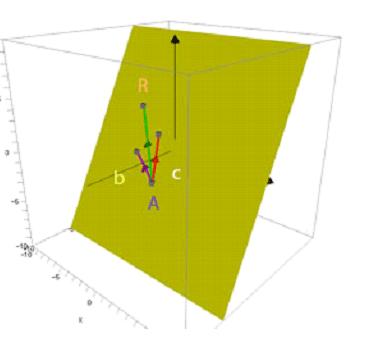
When A is a known point on the plane,
R is any old point on the plane and b and c are vectors
parallel to the plane,
the vector equation of the plane is
r=a+λb+μc
The equations of a line
A line can be described when a point on it and
its direction vector – a vector parallel to the line – are known.
In the diagram below, the line L passes
through points
A(x1,y1,z1) and P (x,y,z).
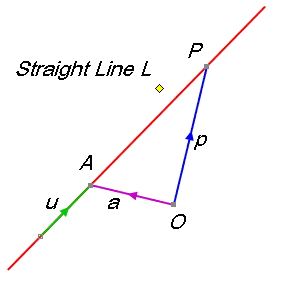
uis the direction vector ai +bj +ck
Being on the line, it has the same direction as
any parallel line.
O is the origin.
a and p represent the position vectors of A and P.
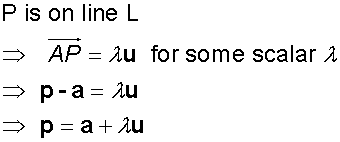
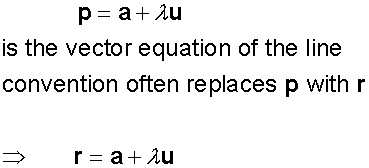
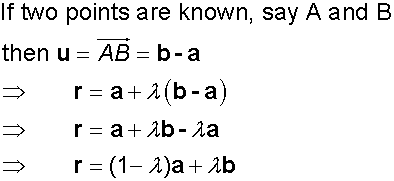
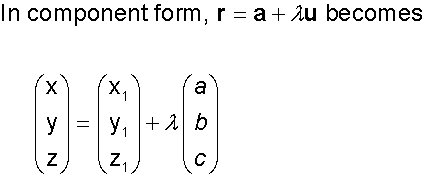
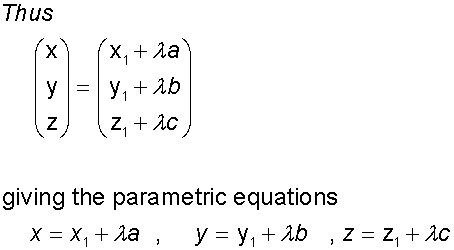
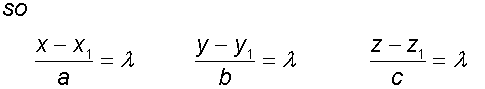

Example
Find the vector equation of the straight line through
(3,2,1) which is parallel to the vector 2i +3j +4k
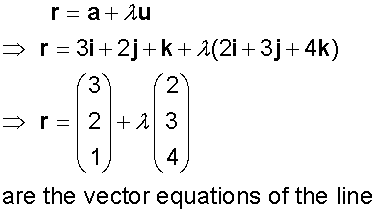
Example
Find the vector form of the equation of the
straight line which has parametric equations
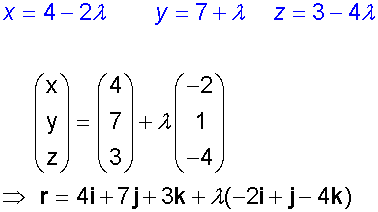
Example
Find the Cartesian form of the line which has
position vector 3i +2j +k and is parallel to
the vector i - j + k
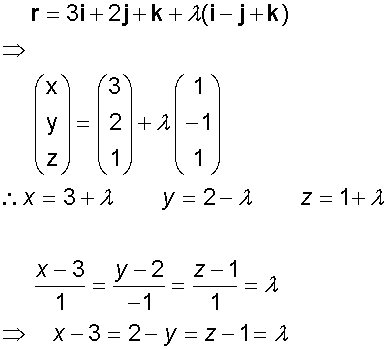
Example
Find the vector equation of the line passing
through A(1,2,3) and B(4,5,6)
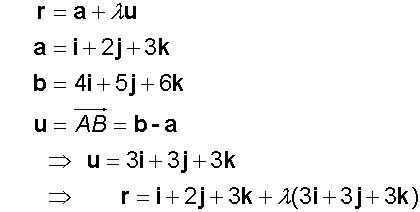
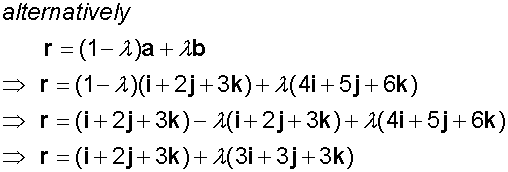
Example
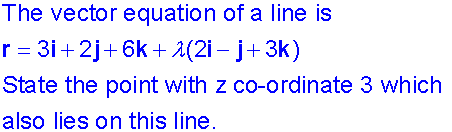
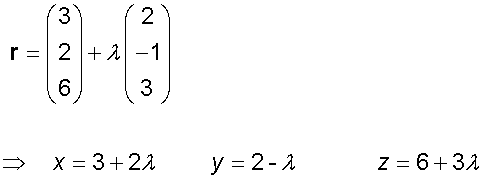
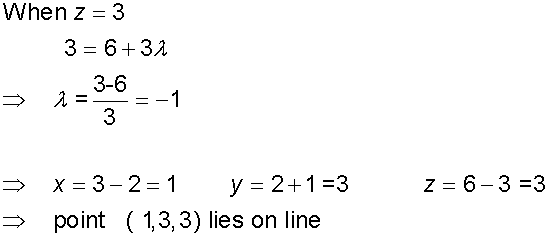
Example
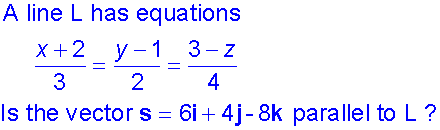
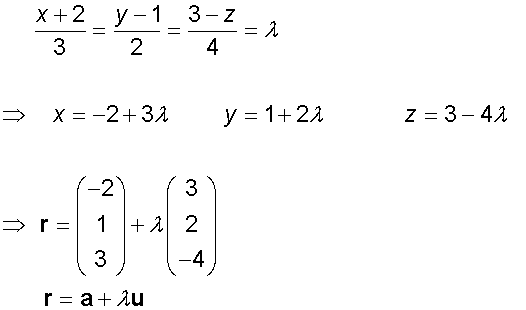

The angle between a line and a plane
The angle θ between a line and a plane is the
complement of the angle between the line and
the normal to the plane.
If the line has direction vector u and the
normal to the plane is a, then
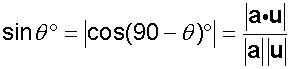
Example

1)
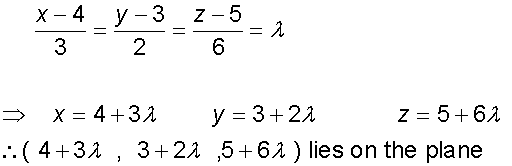
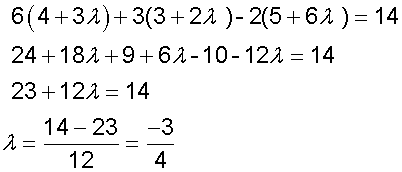
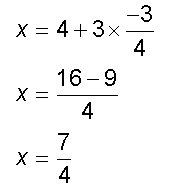
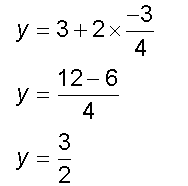
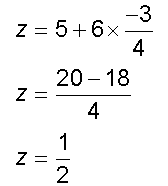

2)
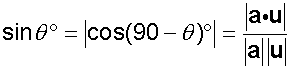
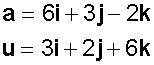
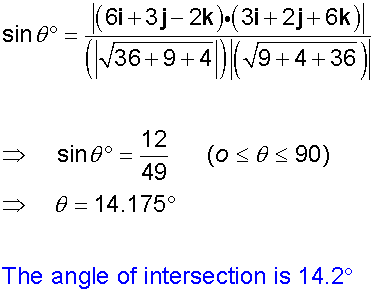
The intersection of two lines
Example

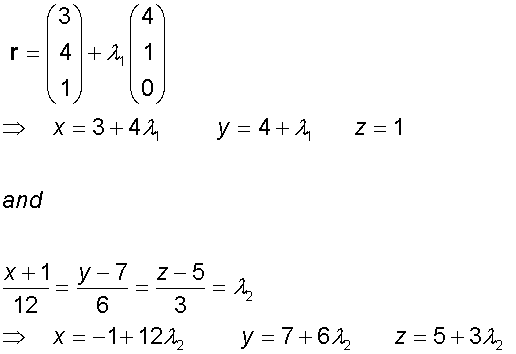
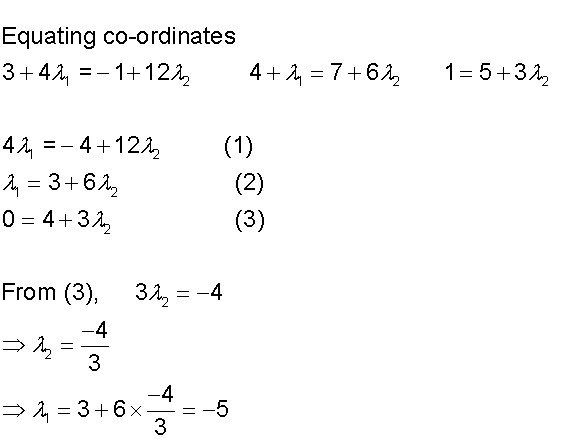
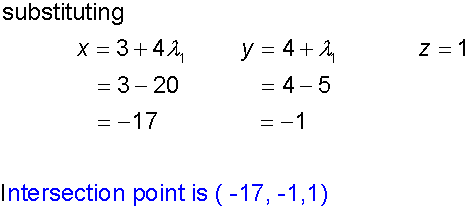
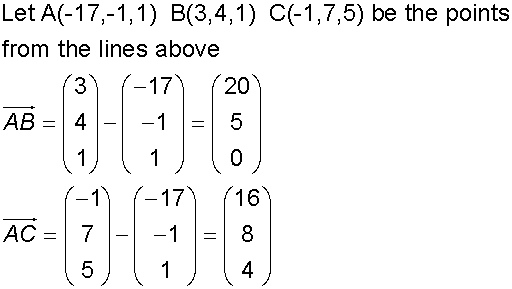
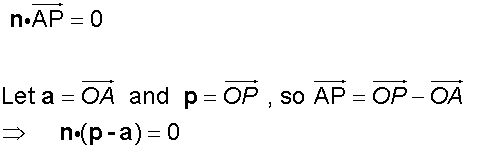
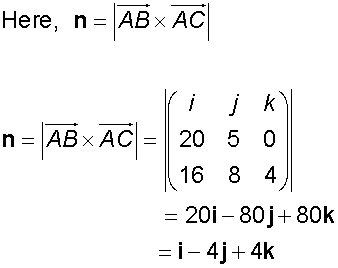
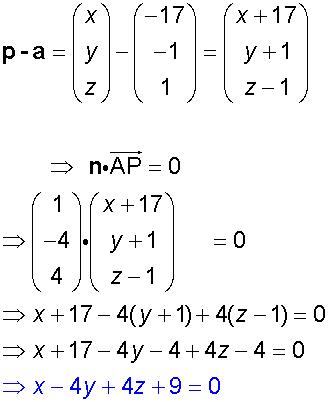
The intersection of two planes
To find the equations of the line of intersection
of two planes, a direction vector and point
on the line is required.
Since the line of intersection lies in both planes,
the direction vector is parallel to the vector products
of the normal of each plane.
Example
Find the equation for the line of intersection
of the planes
-3x + 2y + z = -5
7x + 3y - 2z = -2
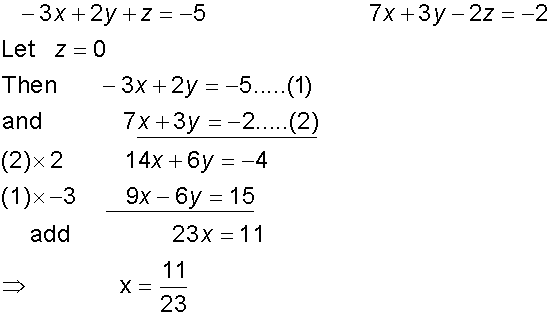
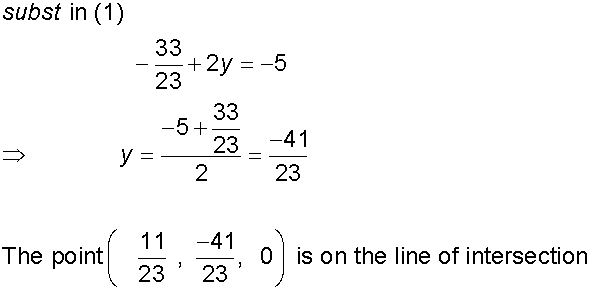
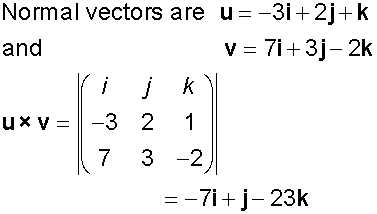
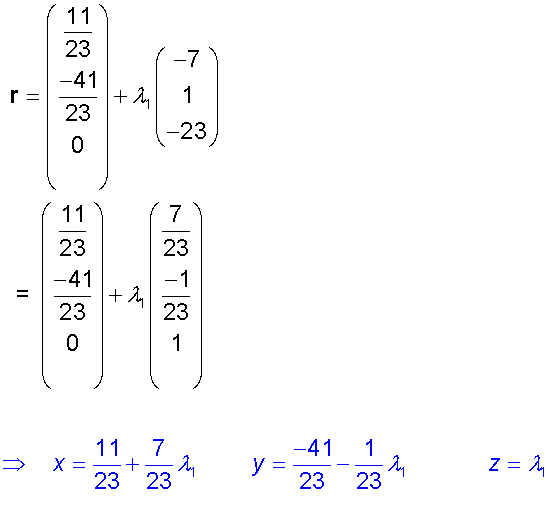
The distance from a point to a plane
To find the distance of a point P to a plane
-
Find the equation of the projection PP’ by using
the normal to the plane and the point P. - Find the co-ordinates of P’ , the intersection
with the plane. - Apply the distance formula to PP’
Alternatively
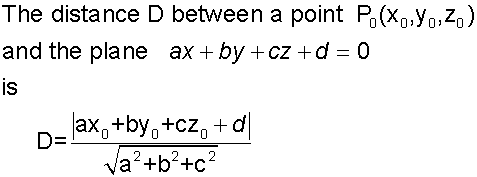
Example
Find the distance between the point ( 3,1,-2)
and the plane x +2y + 2z = - 4
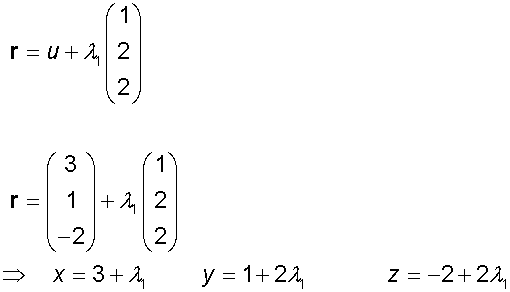
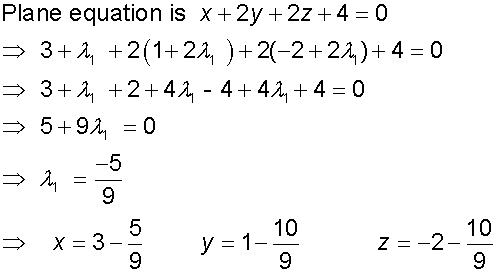
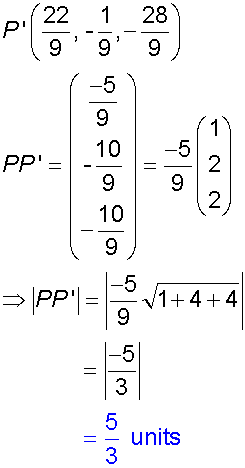
Alternatively
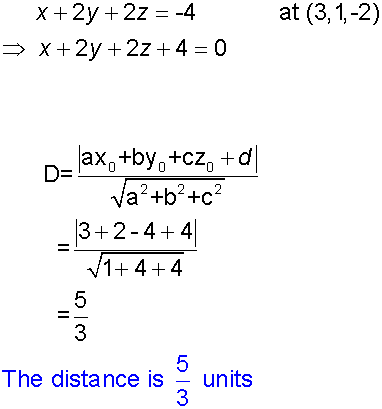
The distance from a point to a line
To find the distance of a point P to a Line L
- Let the line have direction vector u and parameter λ
- Find the co-ordinates of PP’ by using the scalar product with u
and the point P. - Apply the distance formula to PP’
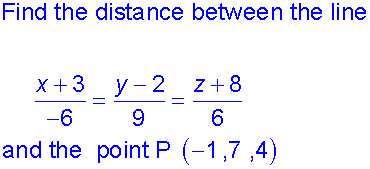
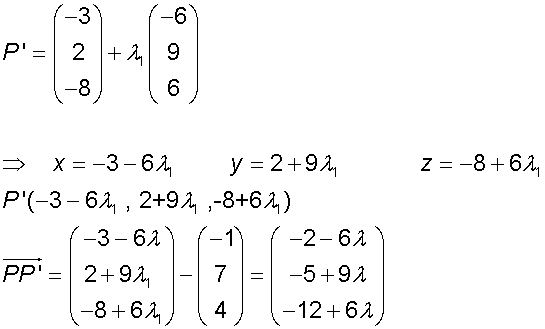
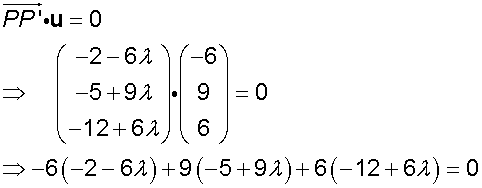
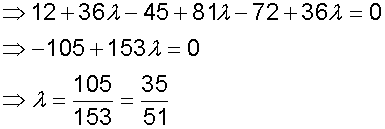
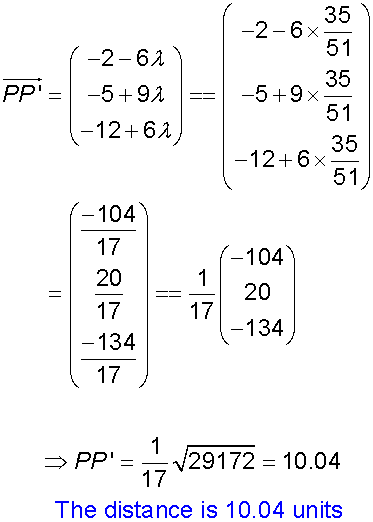
The intersection of three planes
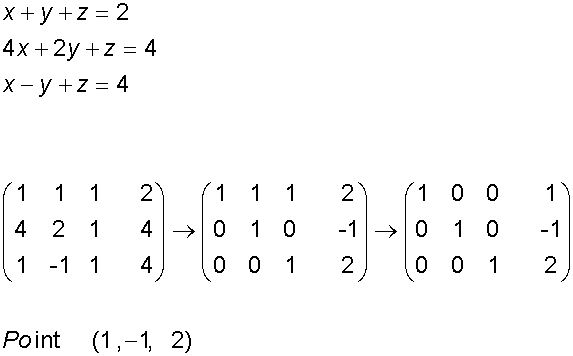
To solve the intersection,
use the equations of the plane ax +by +cz +d = 0
to form an augmented matrix, which is solved
for x, y and z.
The intersection between three planes could be:
A single point
A unique solution is found
Example

A line of intersection
An infinite number of solutions exist
Example
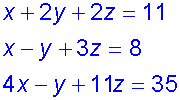
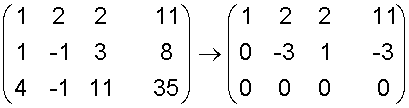
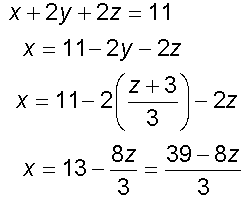
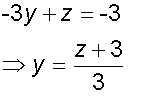
![]()
Parametric equations

Two lines of intersection
An infinite number of solutions
Example
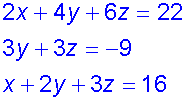
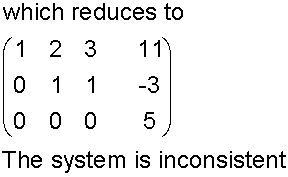
Using the second row
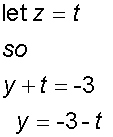
Substitute into first row
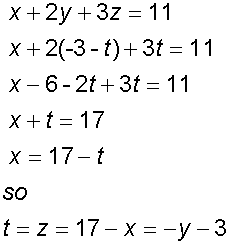
Substitute into third equation
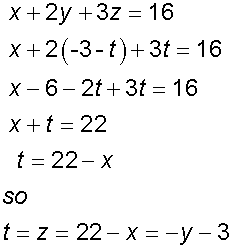
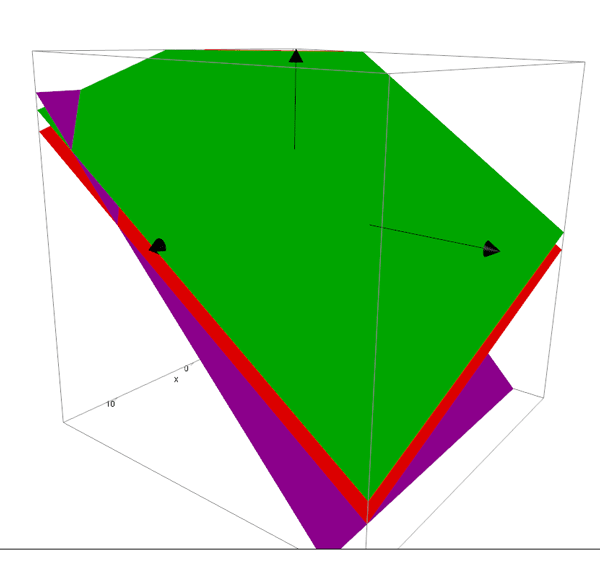
Three lines of intersection
Similar to above.
Examine each pair of planes in turn.
Example
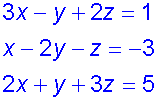
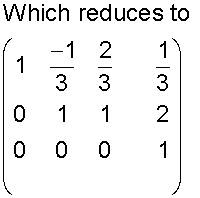

A plane of intersection
Two redundant equations
Example
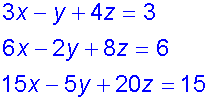
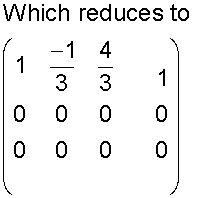
No consistency
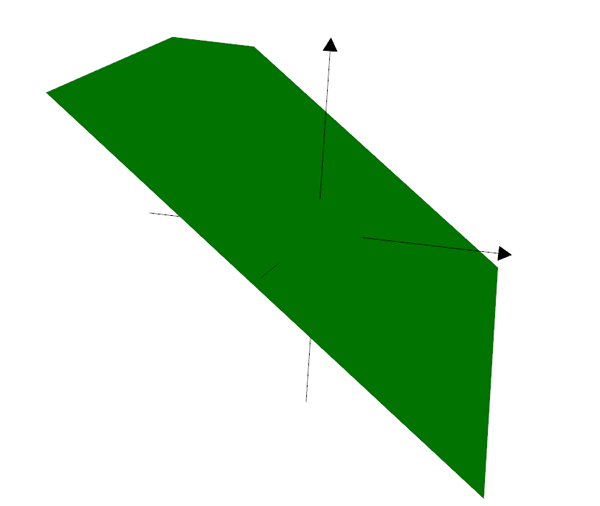
No intersection
Example
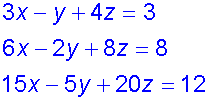
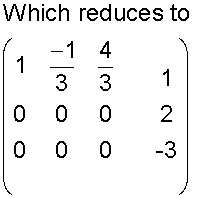
No consistency
All planes are parallel