Perpendicular means to cross at right angles.
To bisect means to cut into two parts of equal shape and size.

Perpendicular bisector

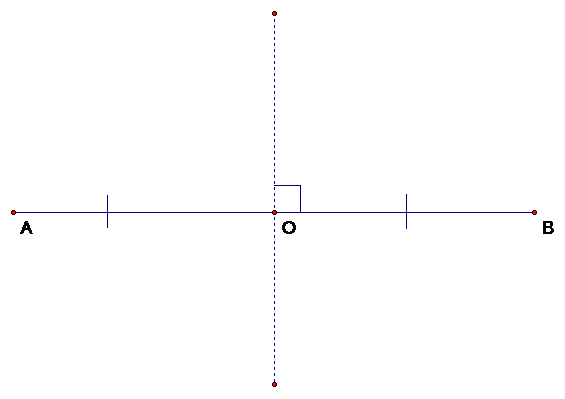
 A perpendicular bisector cuts a line in half at 90 degrees.

Example

Find the equation of the perpendicular bisector
of the line joining A(0,3) and B(5,4)

  

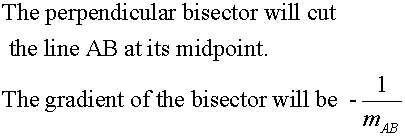
Find the Midpoint of AB

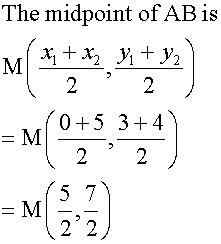
Use this to find the gradient

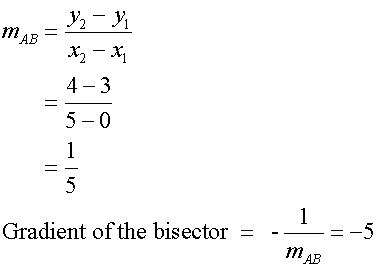
Now find the equation

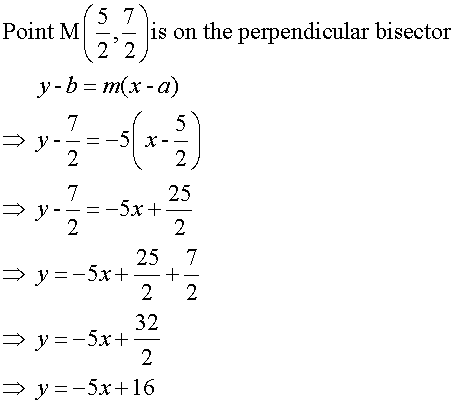
Concurrency

Lines are said to be concurrent if they pass through one common point.

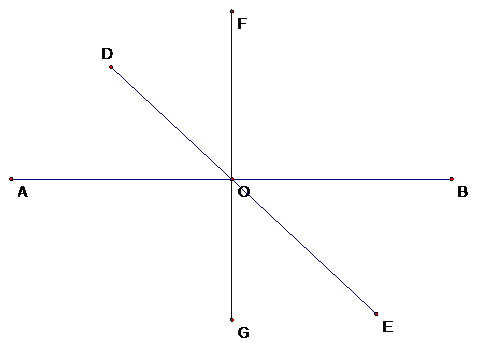
Lines AB, DE and FG are all concurrent, sharing the common point O.
The perpendicular bisectors of a line are concurrent.

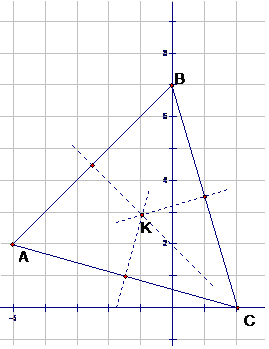
Circumcentre

In a triangle, the point of intersection of the perpendicular bisectors is called the circumcentre.

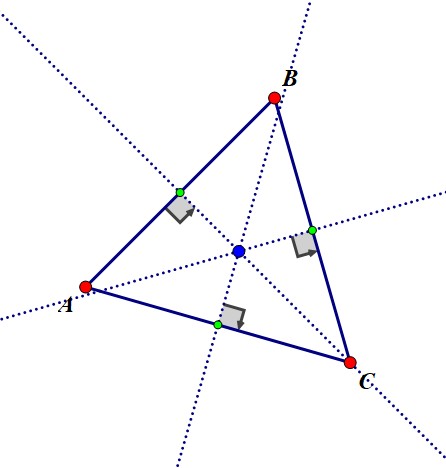
The circumcentre is equidistant from the three vertices.

 

Circumcircle

The circumcircle of a triangle is the circle which passes through all the vertices of the triangle and has its centre at the circumcentre.

 

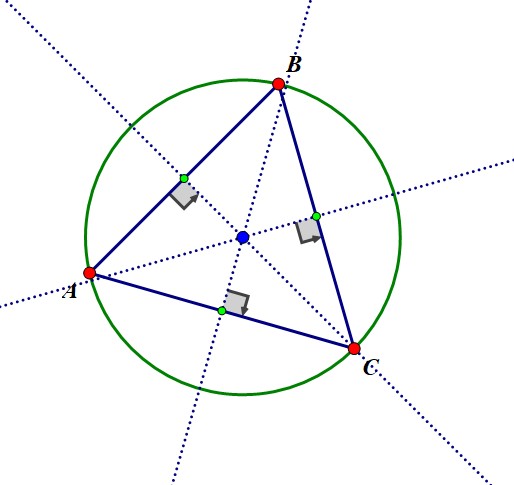
Example

Find K, the circumcentre of the triangle formed by the points
A(-5,2) , B(0,7)  and C (2,0)

          Steps

• Find Midpoints
• Find gradients
• Solve equations to find K.

Solution:

The midpoints are

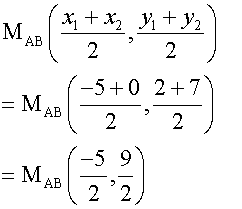
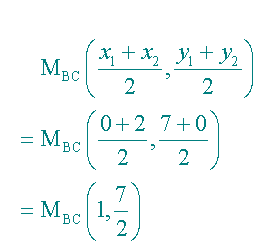
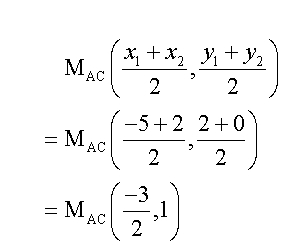
Now find the gradients

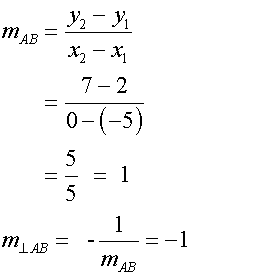
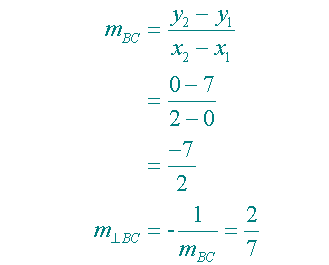
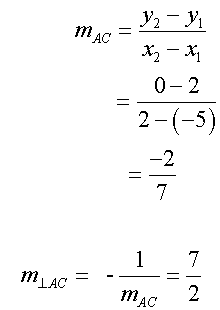
To get the equations of the perpendicular bisectors

 

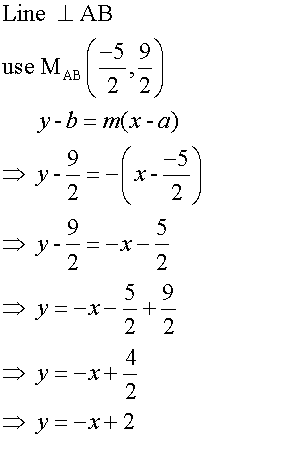
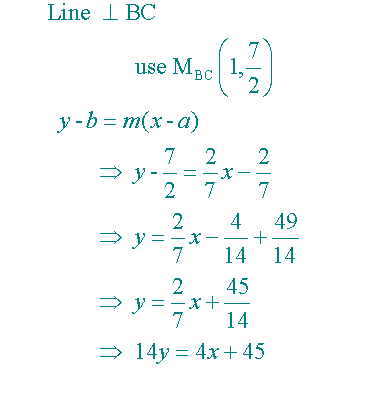
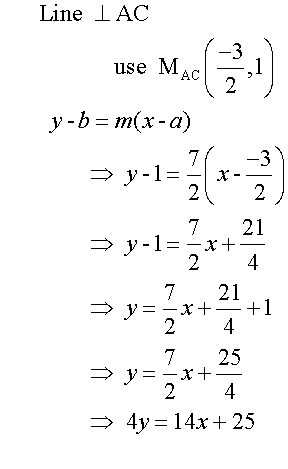
Now solve the sets of equations

 

 

 

 

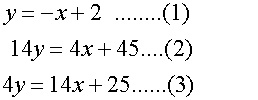
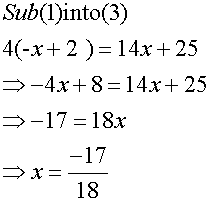
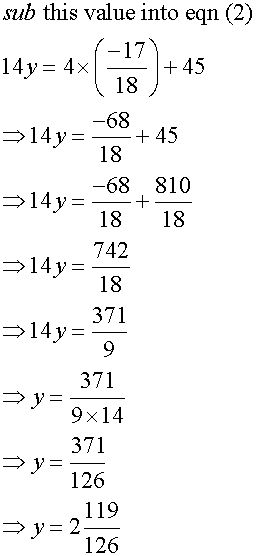
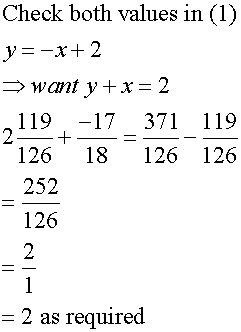
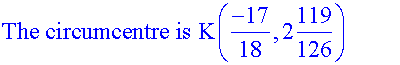
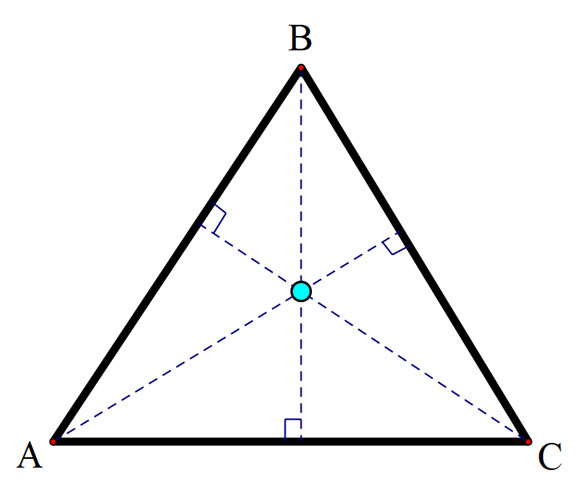
Altitude

An altitude of a triangle is a line drawn from a vertex perpendicular to the opposite side. Since a triangle has three sides, it also has three altitudes.
The altitudes are concurrent and meet at the orthocentre of the triangle.

 

 

 

Example

 

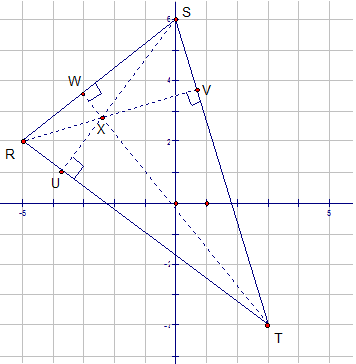
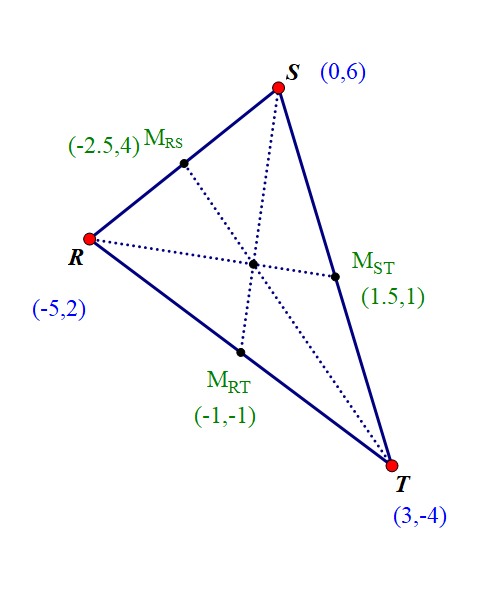
Triangle RST has co-ordinates
R(-5,2) , S (0,6) and T( 3,-4)

Find the equation of the altitude from S.

 

Solution

The altitude from S is perpendicular to RT.

 

 

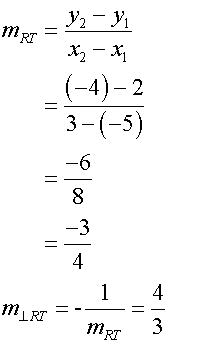
Median

A median of a triangle is a line from a vertex to the midpoint of the opposite side.

A triangle has three medians, which cross at the centroid.

 

 

 

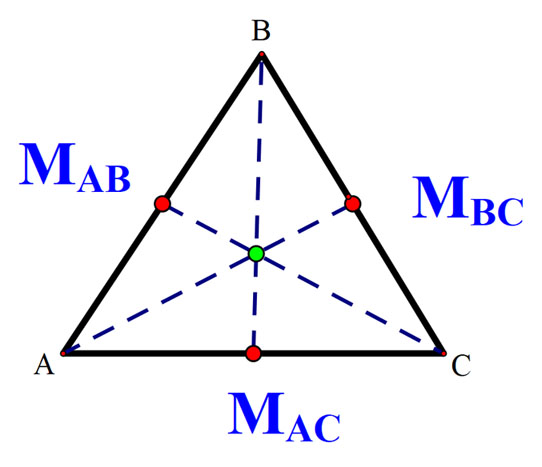
The Centroid splits the median in the ratio 1:2

 

Example

Triangle RST has co-ordinates
R(-5,2) , S (0,6) and T( 3,-4)

1. Find the equation of the median from R.
2. Find the equations of the median from S.
3. Find the equation of the median from T.
4. Hence find the centroid of triangle RST

 

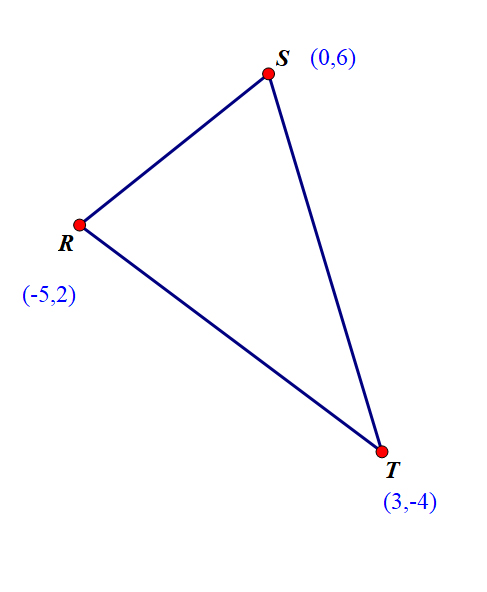
1.

First, find the midpoint of ST

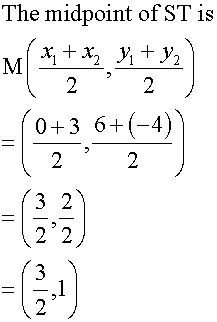
Now find the gradient of this line

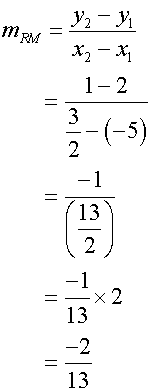
Use to find equation

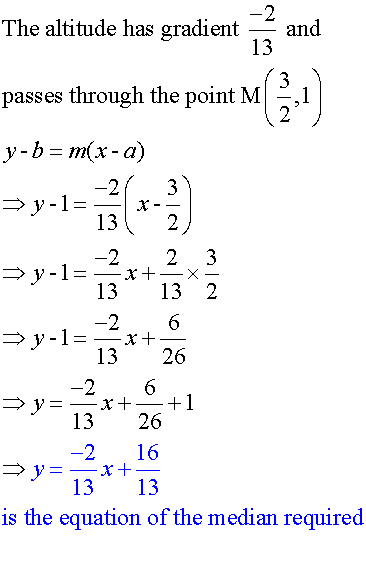
The median from R has equation

     13y = -2x +16

 

2. Repeat for S

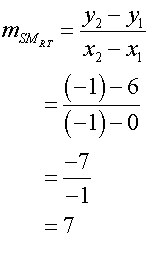
The median from S has equation

     y = 7x +6

3. Repeat for T

 

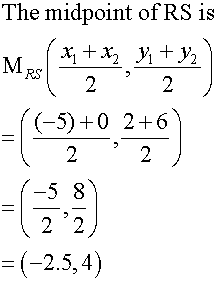
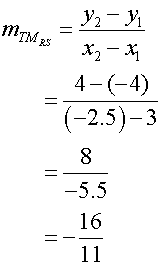
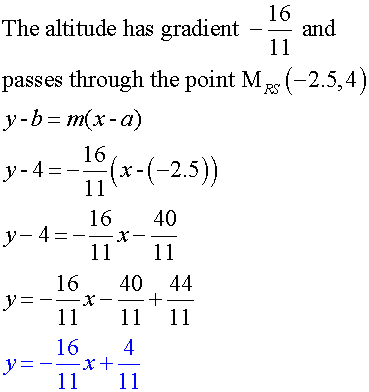
The median from T has equation

   11y = -16x + 4

4. Centroid is at the intersection of the three medians.

Equating medians from R and S gives

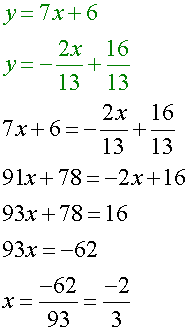
or Equating medians from T and S gives

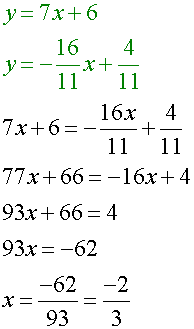
or Equating medians from R and T gives

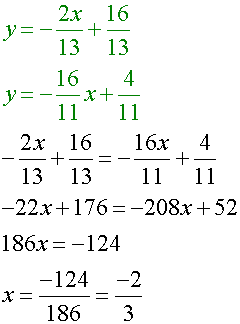
To find y, substitute x = -2/3 into a median equation :

or

   

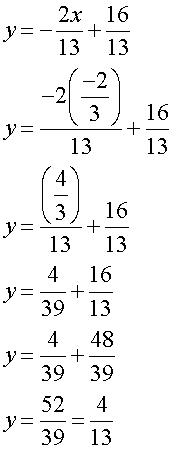
or

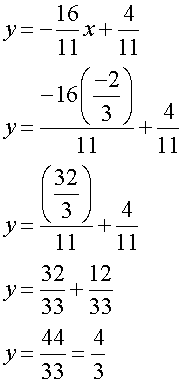
Centroid is at ( -2/3 , 4/3 )