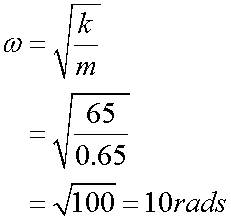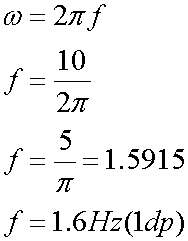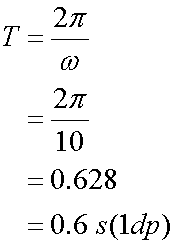Simple Harmonic Motion

Harmonic motion occurs when a particle undergoes oscillating or periodic motion. The frequency of the motion is the number of oscillations per second. The SI unit for frequency is the hertz (Hz), which is 1 oscillation per second.

The period of the motion, T, is

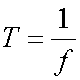
where f is the frequency.

Simple harmonic motion occurs when the magnitude of the acceleration of the particle is proportional to the distance from the fixed point and acts in the opposite direction to the displacement. Simple harmonic motion is sinusoidal.

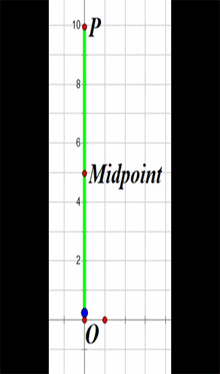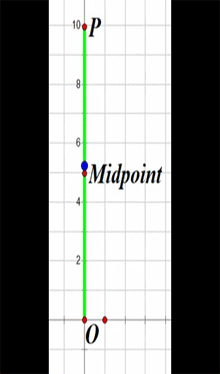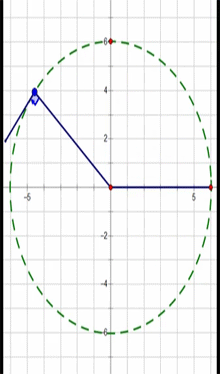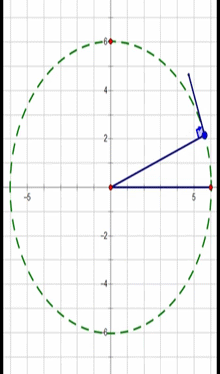
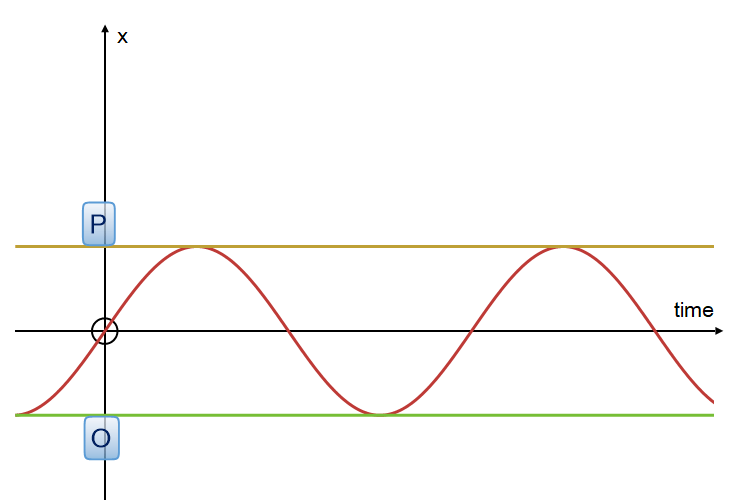
As the particle moves from P to O and back again, its motion in the x direction can be graphed as a function of time :

Speed is the magnitude of velocity, which is the rate of change of displacement with time.

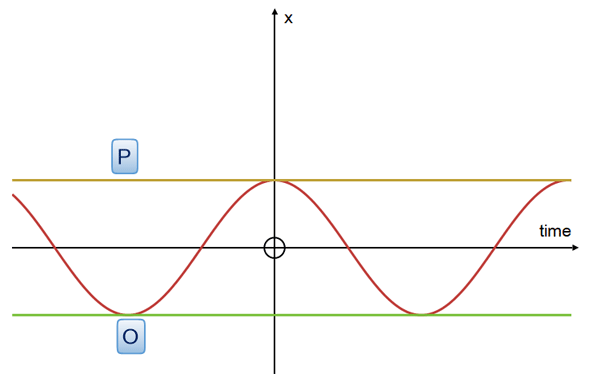
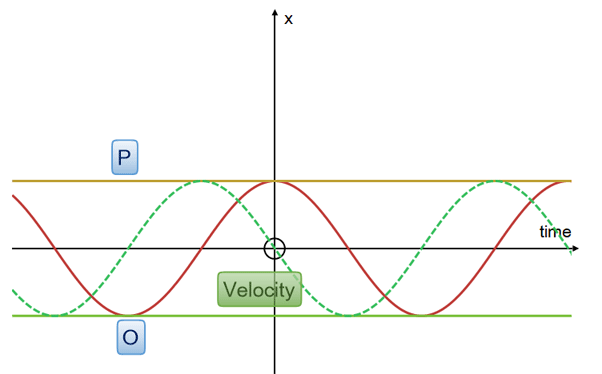
The particle's speed is greatest at the midpoint and zero at points O and P.

Acceleration is shown as the blue line.

 

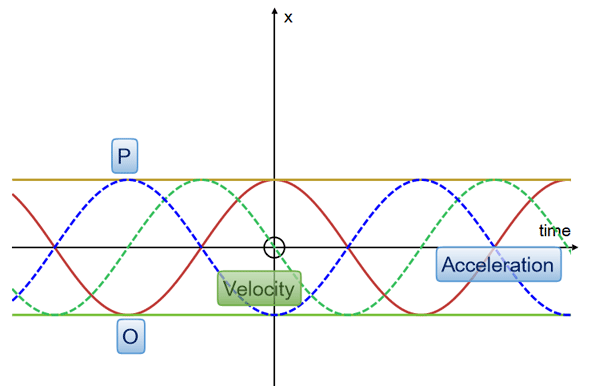
The displacement is a cosine graph.

 

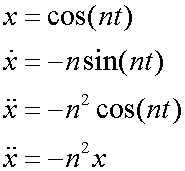
The following represents the displacement of the particle from the midpoint in the x direction as it bounces between the limits O and P. Timing is started at the midpoint, with the particle headed towards P.

 

 

 

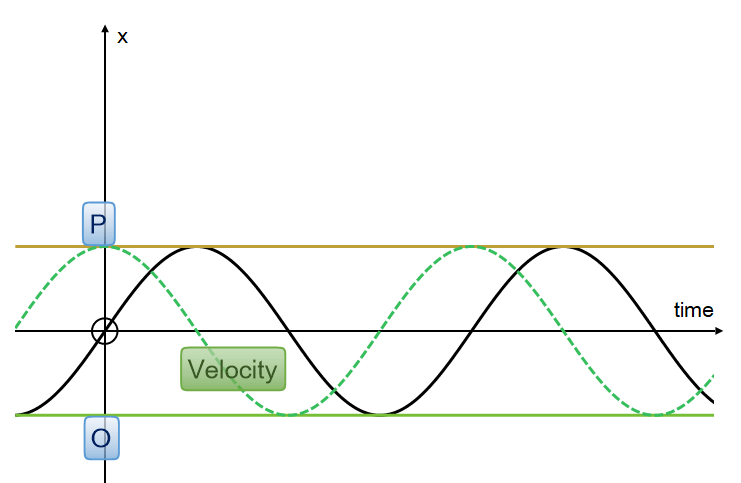
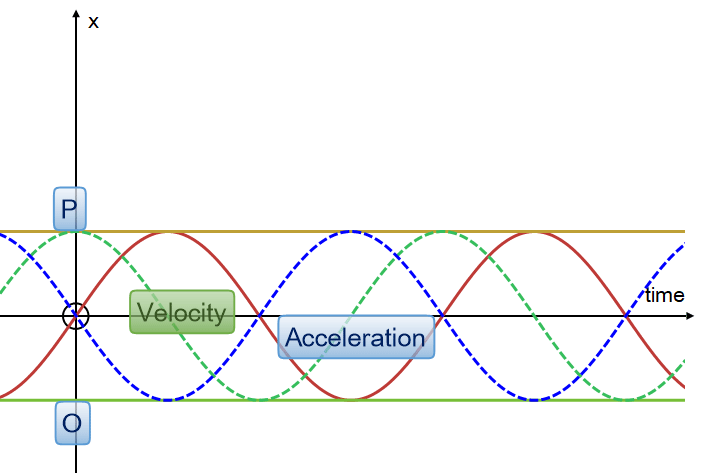
The displacement is a sine graph.

 

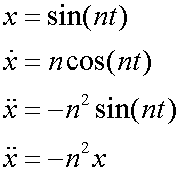
In either case,

Which gives the differential equation

or

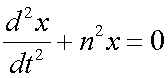
where n is the number of cycles in the period.

As the particle moves, the angle moves.

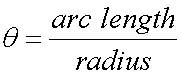
The difference between the old and new angle is called angular displacement:

The rate of change of angular displacement is called angular frequency.

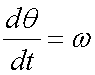
Since simple harmonic motion is sinusoidal,

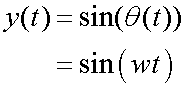
The period is

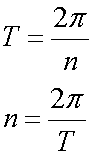
This can be written as

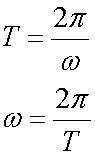
and substituted into

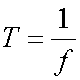
giving

 

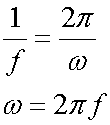
Working backwards

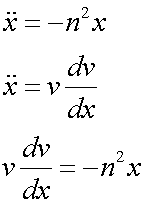
so

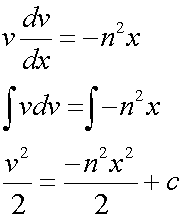
Further, when v = 0, the particle is at a maximum or minimum. The displacement is equal to the amplitude, a.

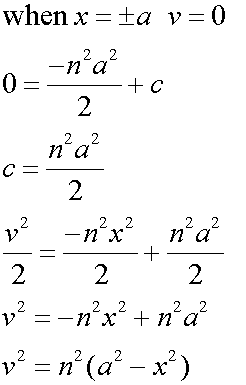
Replacing n with ω

Since the maximum speed occurs when the particle is at the midpoint,

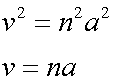
or

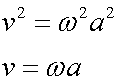
also

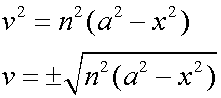
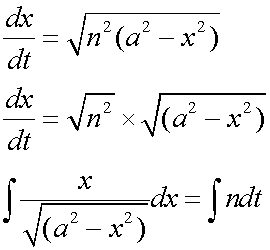
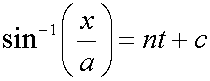
renaming the constant of integration as ε gives

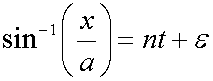
Further,

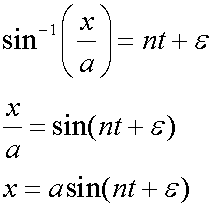
so

or

Where ε is the phase angle, a is the amplitude and n is the number of cycles in the period. (ω is the angular frequency.)

The velocity is

or

Where ε is the phase angle.

 

Force Law for Simple Harmonic Motion

 

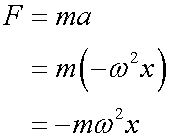
compare to Hooke's Law

The spring constant is

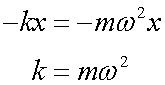
so

 

 

 

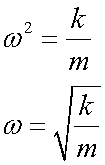
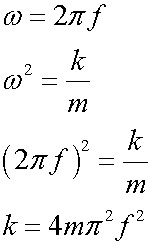
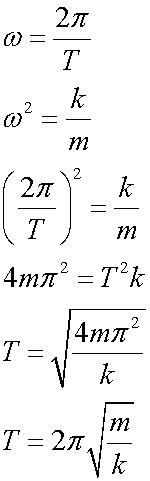
Example

 

A tub of mass 650g is attached to a spring with spring constant 65 N/m. The tub is displaced 11cm from its equilibrium position of x = 0 and released at time t = 0.

Calculate the angular frequency, frequency and period of the motion.