Sets

A mathematical set is a collection of distinct objects, such as numbers, letters, shapes, or functions. The objects in a set are called its elements or members. Sets can be defined by listing their elements between curly braces, or by using a rule or a description that specifies the criteria for membership.

The set {1, 2, 3} contains only the numbers 1, 2, and 3 as its elements.

The set {x : x²} contains square numbers as its elements.

Set Notation

 

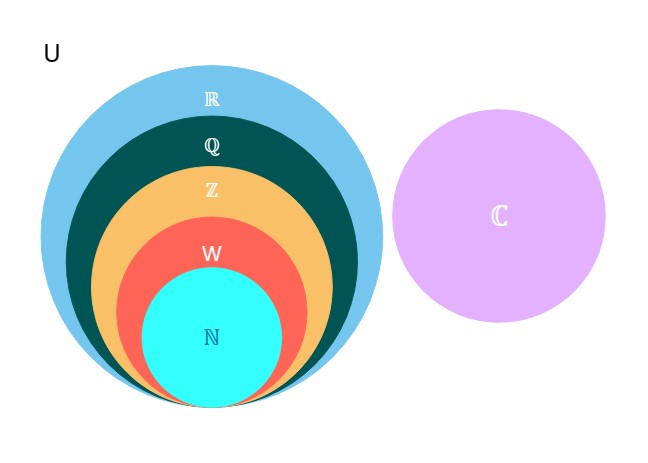
Common Sets

 

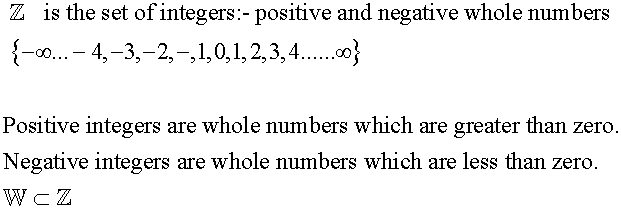
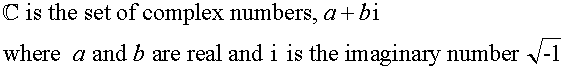
Examples

List the sets defined by

 

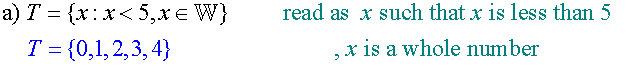
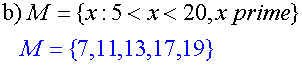
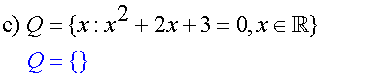
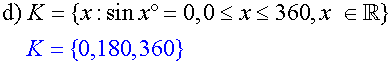
Venn Diagrams

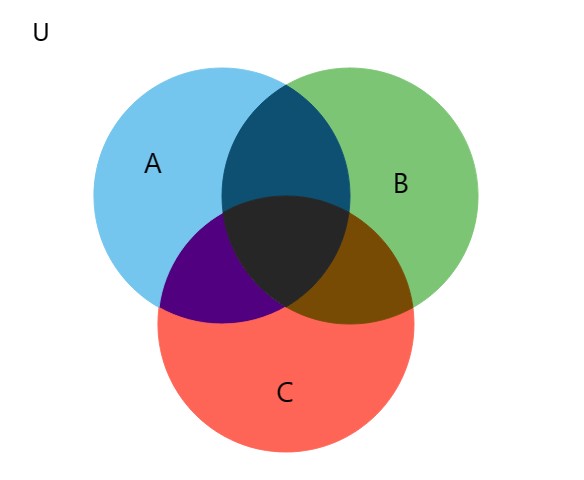
Venn diagrams are graphical representations of the relationships between sets of elements. U represents the Universal set

A U B : The union of sets A and B

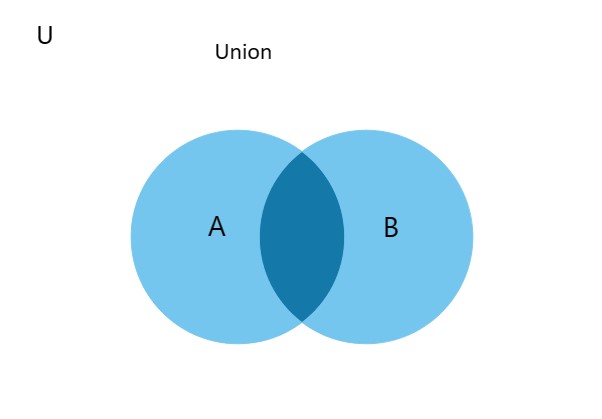
The joining of sets A and B

 

A ∩ B The intersection of sets A and B

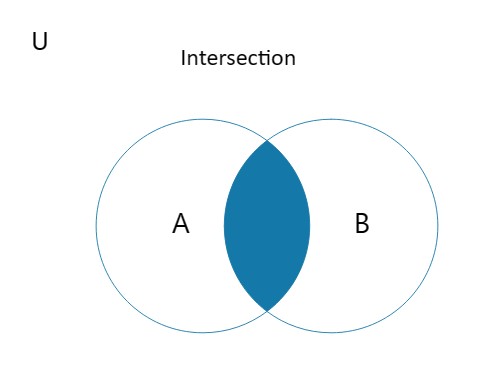
The elements that are in both A and B

 

 

A C B The complement of B ( aka B')

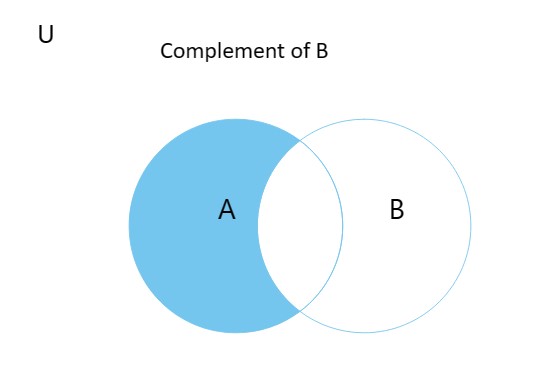
The elements not in set B

 

A - B The difference of A and B

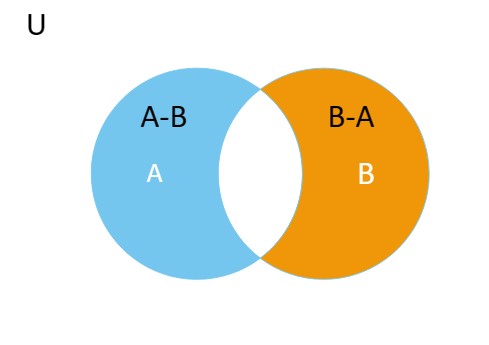
The elements in Set A that are not in set B

 

Mutually exclusive : can't happen at same time

 

Not just two sets!

 

Example

50 people were asked if they had dogs or cats

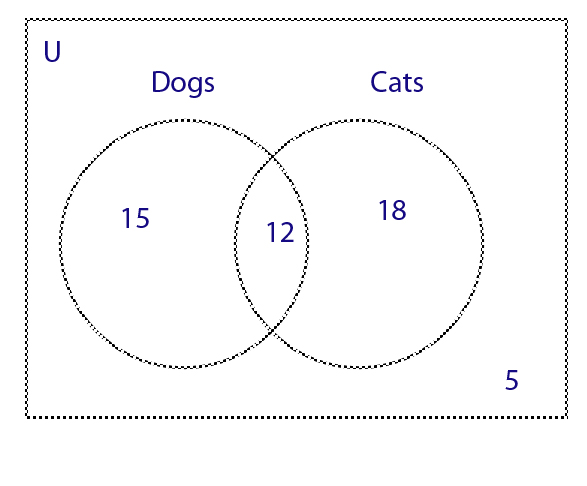
27 people had dogs , 30 people had cats, 5 people didn't have dogs or cats at all.

15 people had dogs only, 18 people had cats only, 12 people had dogs and cats ,

Let set A be dogs and set B be cats

A U B : Union of dogs and cats : 15 +12 +18 = 45

A ∩ B :Intersection of dogs and cats : 12

A C B : The complement of cats , so 50 - 30 = 20

B C A : The complement of dogs , so 50 - 27 = 23

Example

A survey of pet owners is shown as a venn diagram

1. How many people had fish ?
2. How many people had both Dogs and Fish only ?
3. How many people took part in the survey ?

1. 12 +3+ 5 + 7 = 27 people had fish
2. 3 people had both dogs and fish only.
3. 16+8+18+3+5+7+12 =69 people took part in the survey.

Probability and Venn Diagrams

Example

A survey was carried out on a sample of 120 pupils :-

• 78 pupils like sweets
• 74 pupils like chocolate
• 53 pupils like cake
• 57 pupils like both sweets and chocolate
• 46 pupils like both sweets and cake
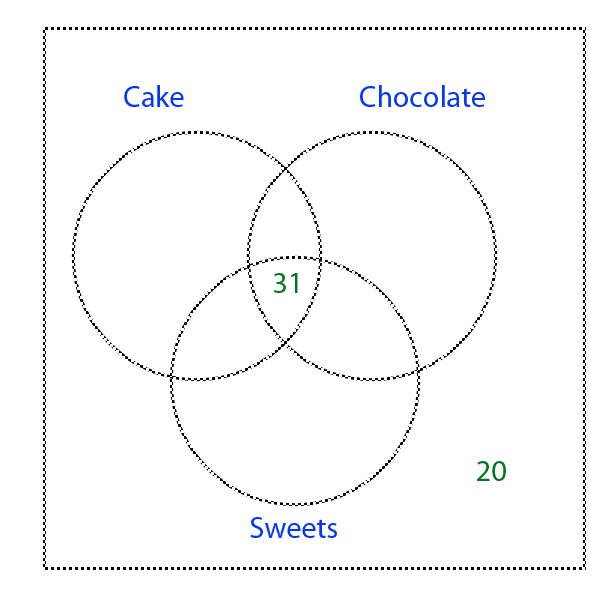
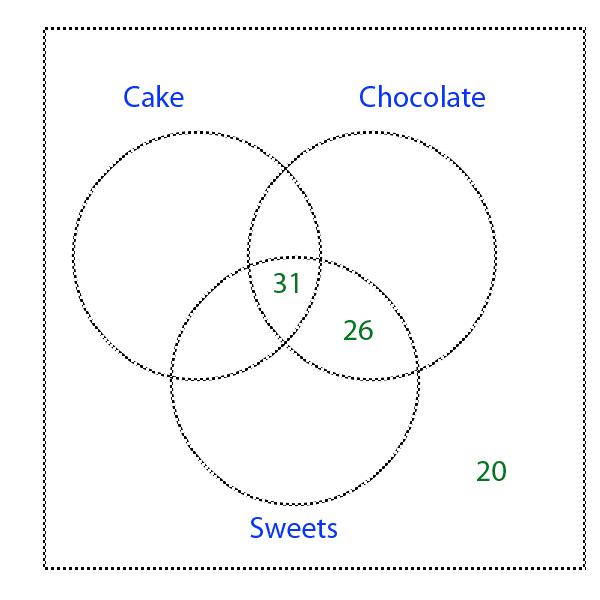
• 31 pupils like sweets, cake and chocolate
• 20 pupils didn't like any of the options.

Complete the Venn diagram to illustrate the results and calculate the probability that a pupil selected at random likes both chocolate and cake.

Firstly, 31 pupils like all 3 options - so 31 can be written in the intersection of the 3 options. The 20 pupils who didn't like any of the options re shown outside the circles .

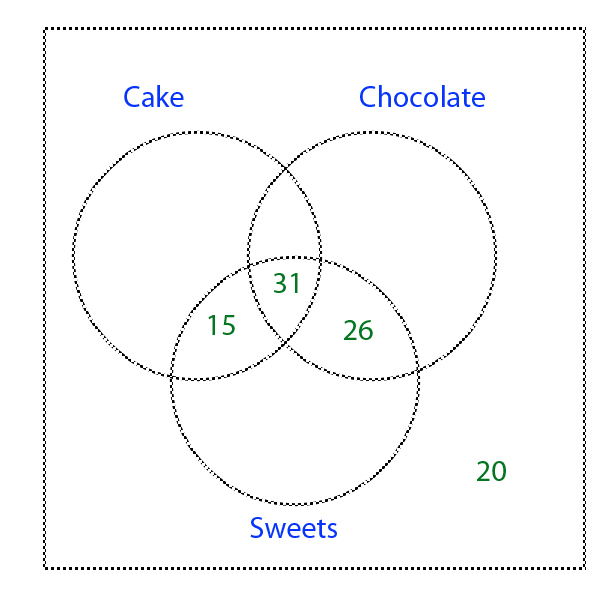
57 pupils like chocolate and sweets, 31 of these have already been accounted for - so 26 can be written in the intersection between chocolate and sweets.

Similarly, 46 pupils like both sweets and cake - so 15 can be written in the intersection between cake and sweets.

 

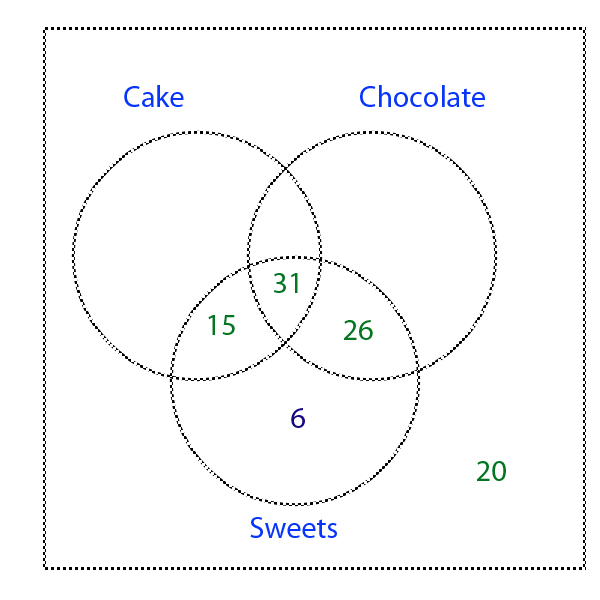
78 pupils like sweets, 15 + 31 + 26 = 72, so 6 must be be written in the sweets only part of the venn diagram.

 

There are now 3 sections left, cake only, cake and chocolate, chocolate only.

Let x = no of pupils who like cake only.
Let y = no of pupils who like cake and chocolate only.
z = no of pupils who like chocolate only

 

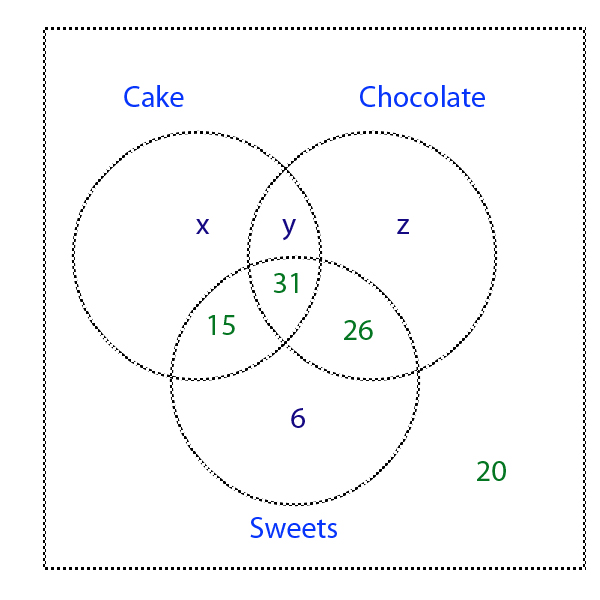
Out of the 120 pupils, 20 didn't like any of the options, so 100 pupils like at least one of the options.

so x + y + z +15+31+26+6 =100 → x + y + z + 78 =100 → x + y +z =22

53 pupils like cake so x + y +15 +31 = 53 → x + y = 7

Substituting x + y = 7 into x + y + z = 22 →7 + z =22 → z =15

15 pupils like chocolate only

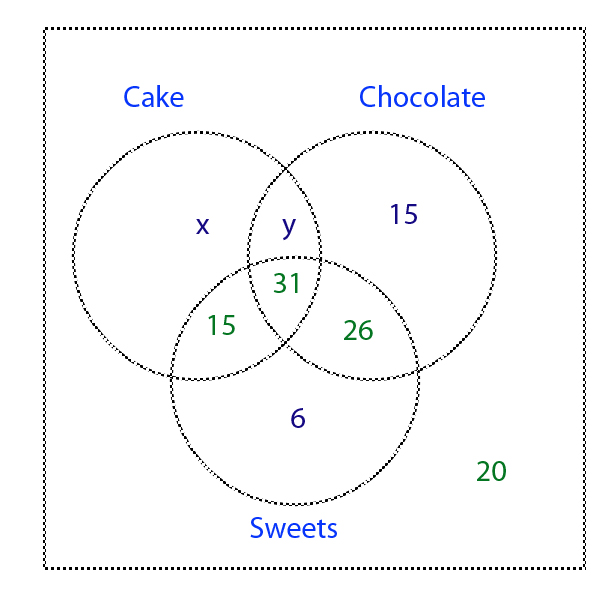
74 pupils like chocolate, so y + z +31+ 26 = 74 → y + z = 17

but z = 15 so y + 15 = 17 → y = 2

33 pupils like cake and chocolate.

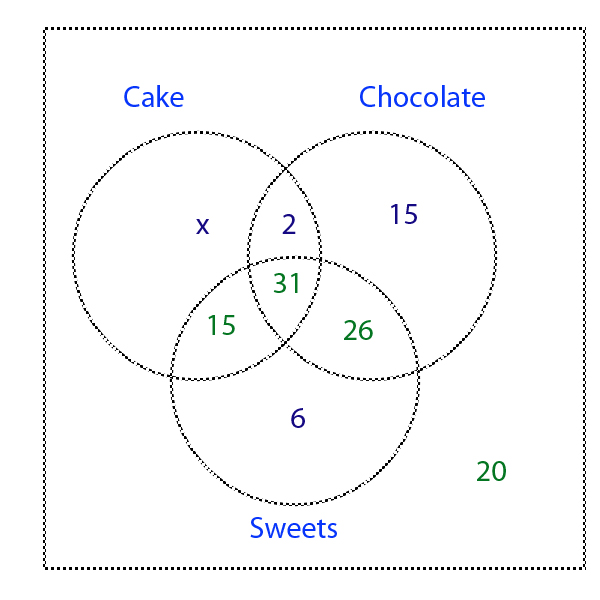
x + y +z =22 → x + 2 + 15 = 22 → x = 22 -17→ x = 5

5 pupils like cake only.

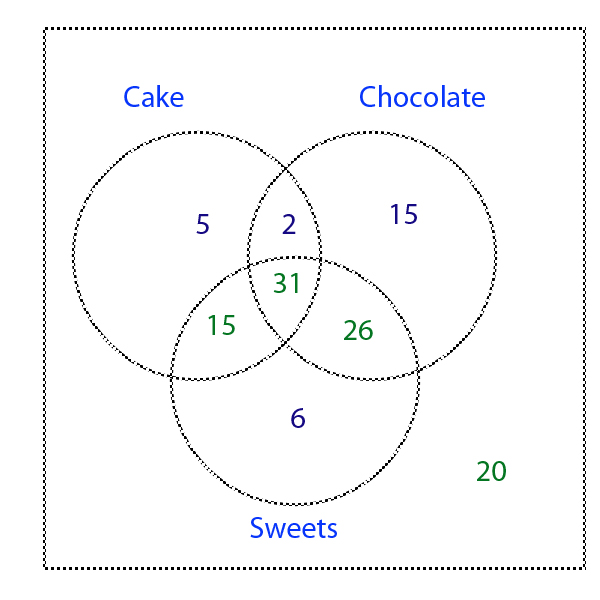
Finally, the probability that a pupil likes chocolate and cake is 33 /120 =0.275 = 27.5%

 

Functions

A function consists of two sets, the domain and codomain,
and a rule which maps each element of the domain
 to exactly one element in the codomain.

The Domain is the set of input numbers,
the Codomain is the set of possible output numbers,
the Range is the set of actual output images.

Example

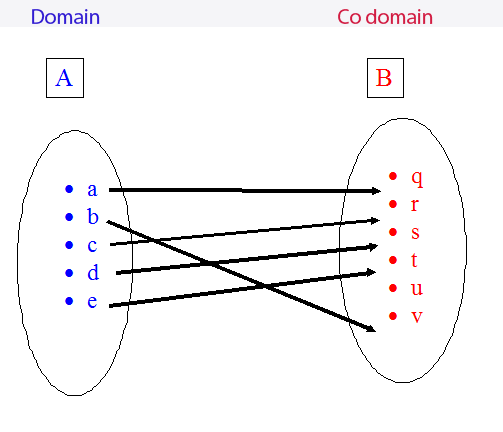
so

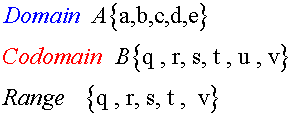
Example

 

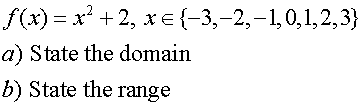
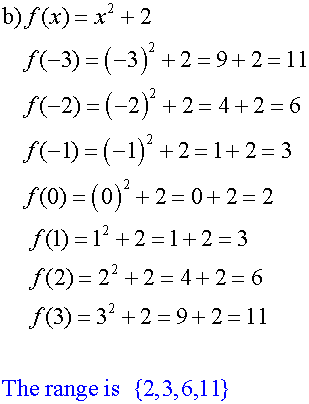
Example

 

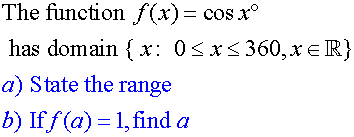
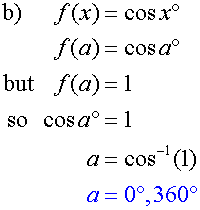
Example
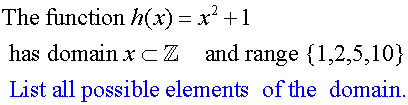
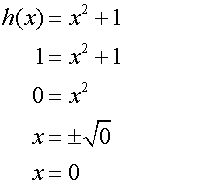
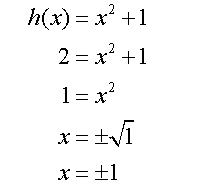
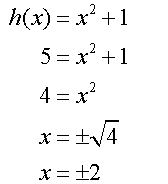
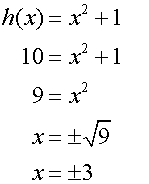