Pythagoras’ Theorem

The longest side of a right‑angled triangle is called the hypotenuse, which is always opposite the right angle.

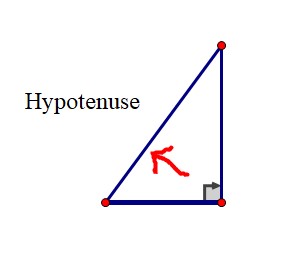
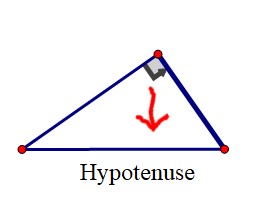
In any right‑angled triangle, the area of the square on the hypotenuse = the sum of the areas of the squares on the other two sides.

For any right‑angled triangle, this rule can be used to calculate the length of the hypotenuse if the lengths of the smaller sides are known.

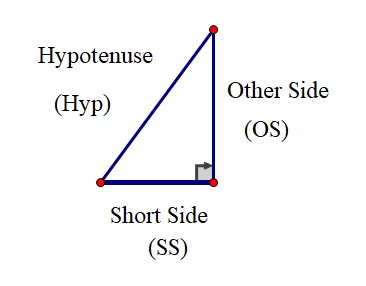
$$ (\text{Hypotenuse})^2 = (\text{Shortest side})^2 + (\text{Other side})^2 $$

To find the length of the hypotenuse

Example

Find the length of the hypotenuse:

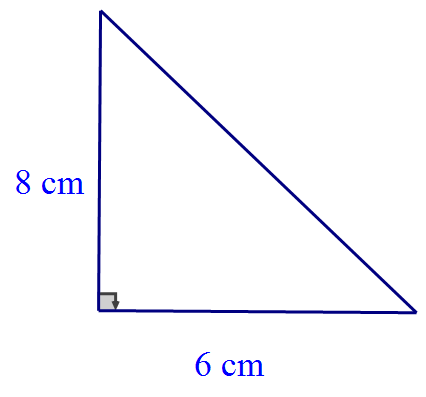
$$ c^2 = 8^2 + 6^2 $$ $$ c^2 = 64 + 36 $$ $$ c^2 = 100 $$ $$ c = 10 $$

Example

Find the length of the missing side:

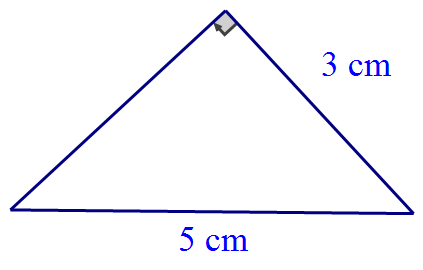
$$ 13^2 = x^2 + 5^2 $$ $$ 169 = x^2 + 25 $$ $$ x^2 = 144 $$ $$ x = 12 $$

$$ (\text{Hypotenuse})^2 = (\text{Shortest side})^2 + (\text{Other side})^2 $$ $$ \Rightarrow \text{The triangle is right‑angled.} $$

Example

Is this a right‑angled triangle?

Do not start by writing out Pythagoras’ Theorem!

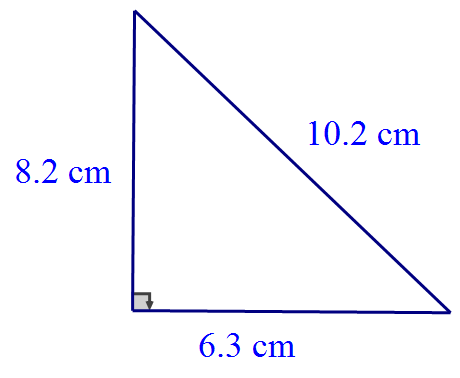
Make separate calculations for hypotenuse and sides.

$$ 10^2 = 100 $$ $$ 6^2 + 8^2 = 36 + 64 = 100 $$ $$ \Rightarrow \text{Yes, it is right‑angled.} $$

Sometimes Pythagoras’ Theorem is needed even when it is not obvious at first.

Example

Calculate the perimeter of triangle ABD.

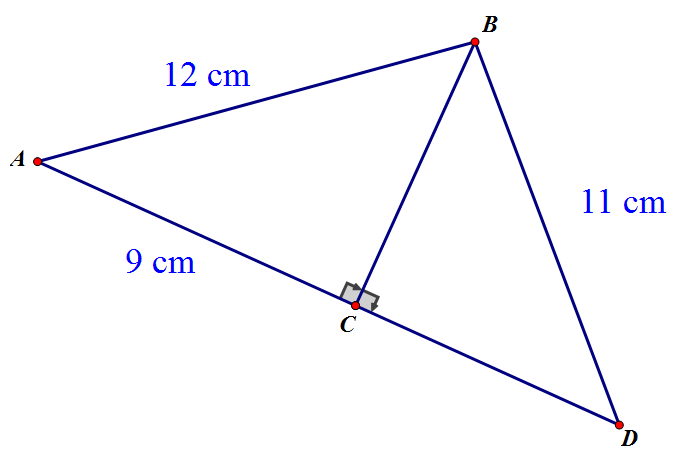
Find BC using triangle ACB, then use triangle BCD to find CD.

$$ BC^2 = 10^2 - 6^2 = 100 - 36 = 64 $$ $$ BC = 8 $$ $$ CD^2 = 11^2 - 8^2 = 121 - 64 = 57 $$ $$ CD = 7.6 $$

Perimeter = 12 + 11 + 9 + 7.6 = 39.6 cm

Example

Calculate the distance between A(-5, 10) and B(3, 0).

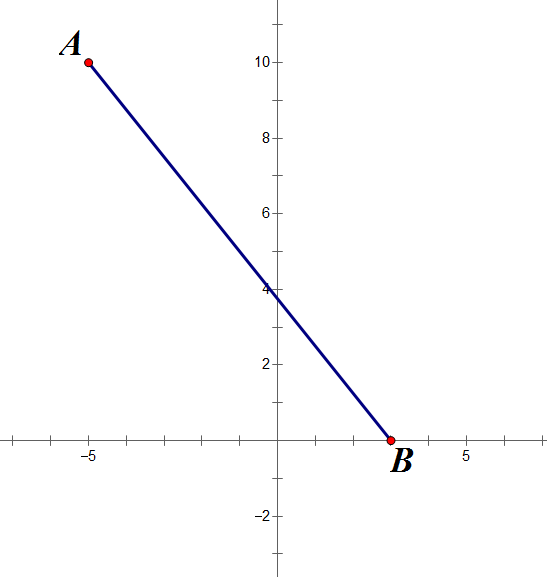
$$ d^2 = (3 - (-5))^2 + (0 - 10)^2 $$ $$ d^2 = 8^2 + (-10)^2 = 64 + 100 = 164 $$ $$ d = \sqrt{164} \approx 12.8 $$

This is the basis of the distance formula.