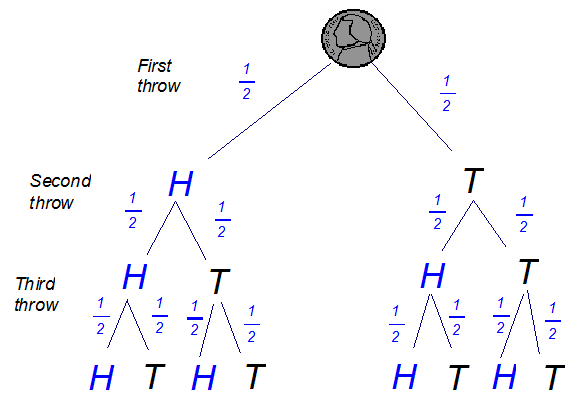
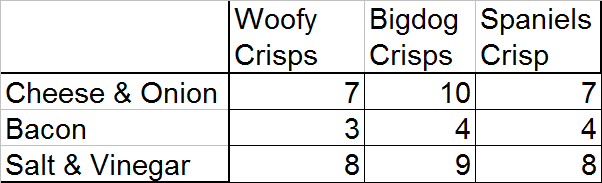
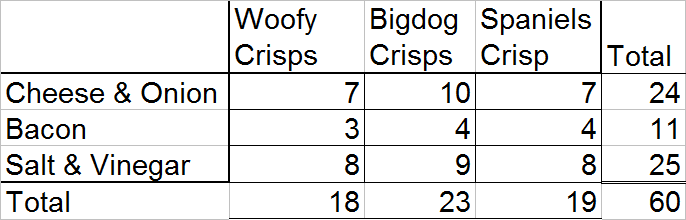
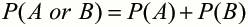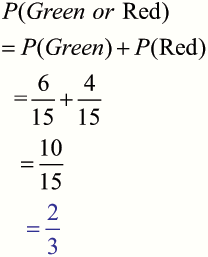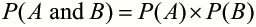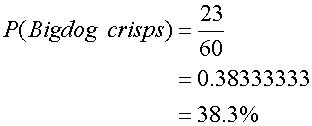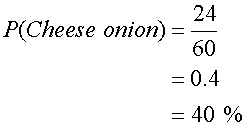Probability

Probability is the chance of something happening.

All probabilities lie between 0 and 1.

Probability can be written as a fraction, decimal or percentage.

Example

An even chance can be written as 0.5, 50% or ½.

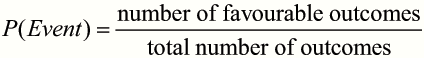
The probability of an event happening is equal to the number of ways an event can happen divided by the total number of possible outcomes.

Example

A bag contains 5 blue, 6 green and 4 red counters.

What is the probability that a counter picked at random will be green?

Example

What is the probability that a card picked at random from a standard pack of 52 cards will be:

A red card?

The probability of picking a red card from a standard deck is:

\( P(\text{Red}) = \dfrac{26}{52} = \dfrac{1}{2} = 50\% = 0.5 \)

An Ace?

\( P(\text{Ace}) = \dfrac{4}{52} = \dfrac{1}{13} = 7.69\% = 0.0769 \)

The King of Spades?

\( P(\text{King of Spades}) = \dfrac{1}{52} = 1.92\% = 0.0192 \)

Mutually Exclusive Events

Mutually exclusive events cannot happen at the same time.

Example

What is the probability that a card picked at random from a standard pack of 52 cards will not be an Ace?

\( P(\text{Not Ace}) = 1 - P(\text{Ace}) \)

\( = 1 - \dfrac{4}{52} \)

\( = \dfrac{52 - 4}{52} = \dfrac{48}{52} = \dfrac{12}{13} \)

\( = 92.3\% = 0.923 \)

Example

A dog shelter has 50 dogs in total. There are 12 Labradors and 8 Poodles. What is the probability that a dog chosen at random is not a Labrador?

We are given the probability of choosing a Poodle, but we do not need it directly — we can simply use the number of dogs that are not Labradors.

\( P(\text{Not Labrador}) = 1 - P(\text{Labrador}) \)

\( = 1 - \dfrac{12}{50} \)

\( = \dfrac{50 - 12}{50} = \dfrac{38}{50} = \dfrac{19}{25} \)

\( = 76\% = 0.76 \)

The Addition Law

This is used to find the probability of two mutually exclusive events happening.

Example

A bag contains 5 blue, 6 green and 4 red counters.

What is the probability that a counter picked at random will be green or red?

The Multiplication Law

This is used to find the probability of two totally independent events happening.

Example

A man is playing a game which involves spinning a wheel.

The wheel has 36 slots, numbered 1 to 36, evenly coloured red or black.

What is the probability that the ball will land on a black number which is between 10 and 20, exclusive?

Tree Diagrams

Probabilities are written on the branches of the diagram and multiplied to give the probability of two events happening.

When there is more than one way of obtaining the desired outcome, the probabilities for each way are added together.

Example

A coin is tossed 3 times.

What is the probability that the coin will land:

• heads up all three times?

• tails up twice only?

Total possible outcomes:

HHH THH

HHT THT

HTH TTH

HTT TTT

Heads up all three times

\( P(\text{HHH}) = \tfrac{1}{2} \times \tfrac{1}{2} \times \tfrac{1}{2} \)

\( = \tfrac{1}{8} \)

\( = 12.5\% = 0.125 \)

Tails up twice only

The outcomes that contain two Tails are: HTT, THT, and TTH.

\( P(\text{Tails Twice}) = P(HTT) + P(THT) + P(TTH) \)

\( = \left(\tfrac{1}{2} \times \tfrac{1}{2} \times \tfrac{1}{2}\right) + \left(\tfrac{1}{2} \times \tfrac{1}{2} \times \tfrac{1}{2}\right) + \left(\tfrac{1}{2} \times \tfrac{1}{2} \times \tfrac{1}{2}\right) \)

\( = \tfrac{1}{8} + \tfrac{1}{8} + \tfrac{1}{8} \)

\( = \tfrac{3}{8} = 37.5\% = 0.375 \)

So the probability of getting exactly two Tails in three flips is 0.375.

Two‑Way Tables

Example

The following table shows the crisps preferences by brand and flavour of 60 people.

Are more people likely to choose Cheese & Onion as a flavour than BigDog Crisps as a brand? Give a reason.

First, add total columns.

Now work out the probability for each part of the question.

There are a total of 23 BigDog Crisps chosen out of 60 bags.

There are a total of 24 Cheese & Onion crisps chosen out of 60 bags.

There is a 1.7% greater chance that Cheese & Onion would be picked as a flavour.

Example

What is the probability of a person choosing a packet of Cheese & Onion flavoured BigDog crisps?