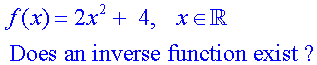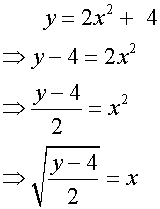One to One functions

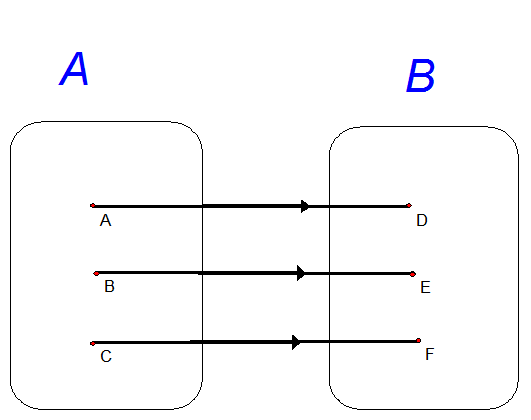
A one-to-one correspondence exists when all of the elements of  set A
 map to exactly one element of set B and vice versa.

          
      This is a one-to-one correspondence.

          
This is a function, but not a one-to-one correspondence.

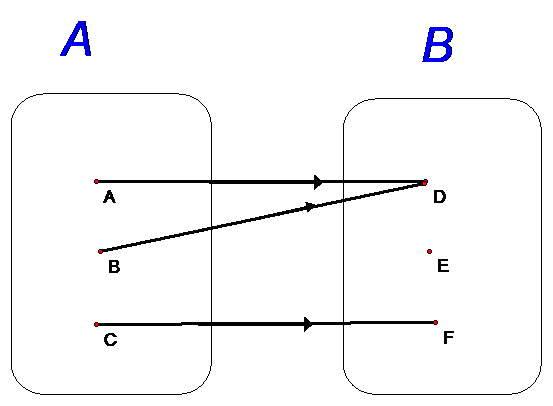
 When a one-to-one correspondence exists,
 the function that maps from set B to set A is called the inverse of f.

 The inverse of a function f(x) is denoted f^-1(x)

    For each element,   f(a) = b  and     f^-1 (b) = a

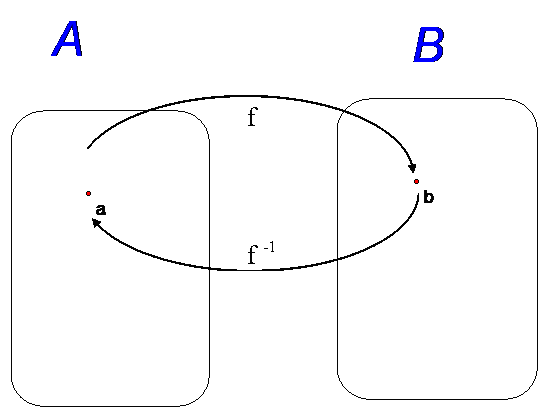
           The domain of f is the range of f^-1
            The range of f is the domain of f^-1

 

f^-1 (f(x)) = f (f^-1 (x)) = x

 

 

Inverse a function

To inverse a function ( which must be in a one – one correspondence)
reflect it in the line y = x.

Example

 Find the inverse of the function   f(x) = 2x + 2   

 
    f(x) = 2x + 2    has graph     y = 2x + 2
    f(0) = 0 + 2 = 2    so the point (0,2) is on the line y = 2x + 2.
    f(-1) = -2 + 2 = 0    so the point (-1,0) is on the line y = 2x + 2.

 

    If this function is reflected in the line y = x,
    the values for x and y are swapped, since y = x and x = y.

   So the point (0,2) becomes ( 2,0)
   and the point ( -1,0) becomes ( 0,-1)

The equation of the reflected line can now be found:-

    

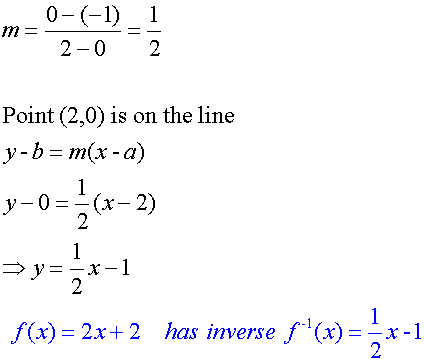
which looks like this:

 

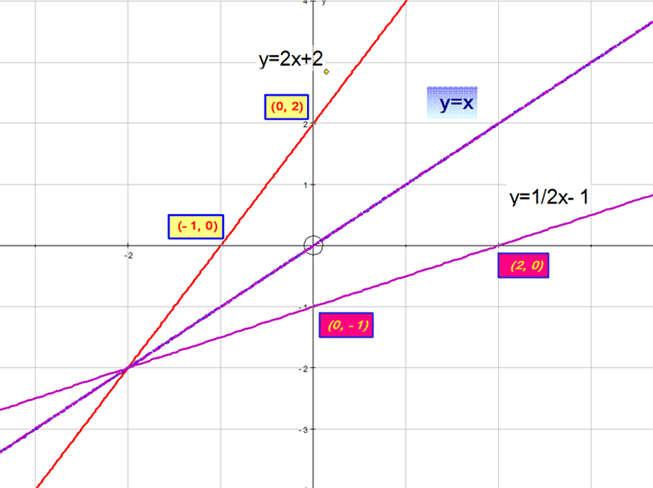
Algebraic method

Example

Find the inverse of the function f(x) = 2x + 2

f^-1 (f(x)) = f (f^-1 (x)) = x

so , substituting for x into f(x) = 2x + 2

2(f^-1 (x)) + 2 = x

Now just re-arrange to make f ^-1 (x) the subject of the formula

2(f^-1 (x)) = x - 2

f^-1 (x) =( x - 2)/2

 so  f ^-1 (x) = ½x – 1

 

Alternatively

f(x) = 2x + 2    has graph     y = 2x + 2
Make x  the subject of the formula   y = 2x + 2

                y = 2x + 2
                y - 2 = 2x
               ½ (y - 2) = x
so            x = ½ (y - 2)

Swap the letters (because of the reflection y = x)

             y = ½ (x - 2)
             y = ½x – 1

 so  f ^-1 (x) = ½x – 1

 

Example

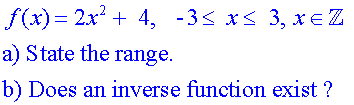
a)

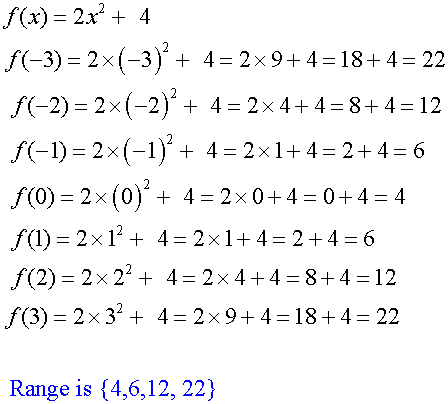
b)

 

Example