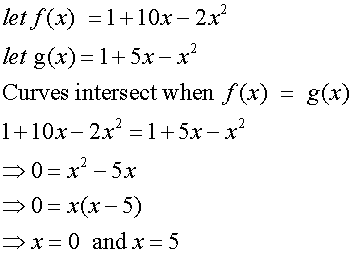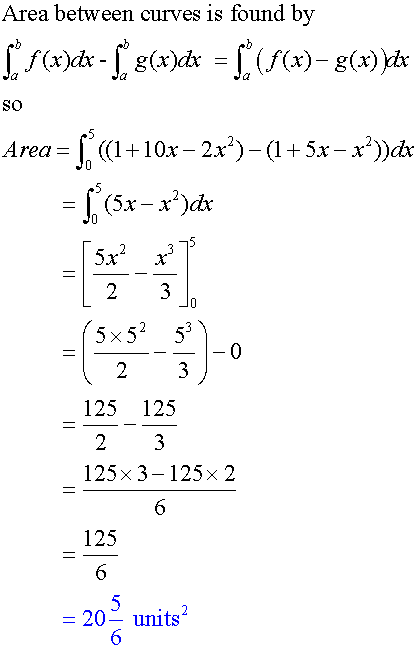Integration and the Area Function

The area between the graph of the function y = f(x) and the x-axis, starting at x = 0 is called the area function A(x)

Example

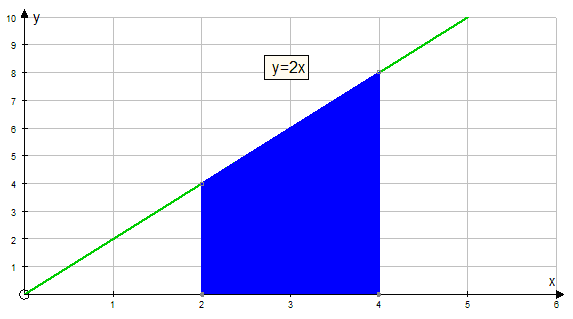
Find the area under the graph y = 2x between x = 2 and x = 4

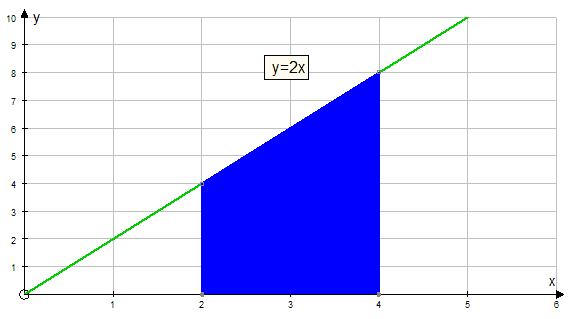
    The area between 2 and 4 can be described as area between x = 0 and x = 4 minus the area between x = 0 and x = 2 y = 2x 

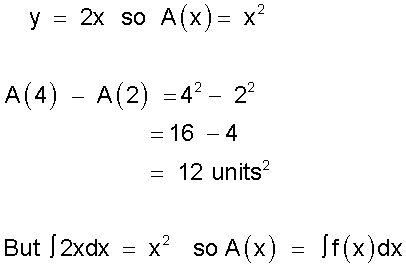
 Definite integrals

 The area of the graph of y = f(x)  between x = a  and x = b   is

    

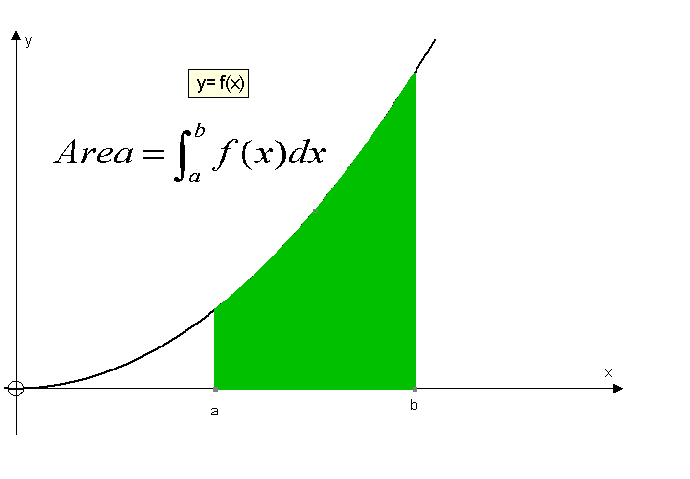
Example

   Find the shaded area as a definite integral.

 

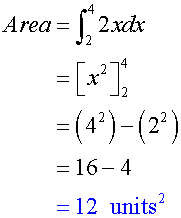
Area between curve and the y-axis

It is sometimes necessary to find the area between the function and the y- axis.

 

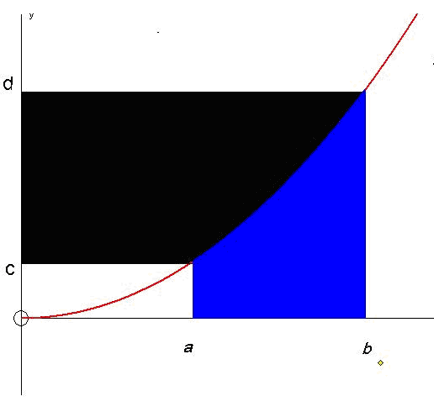
This is given as

 

It is not always possible to express the function y=f(x) in terms of x=f(y).

It may also be easier to calculate

 

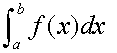
and subtract this as a composite area.

 

Fundamental theorem of calculus

 

   

 

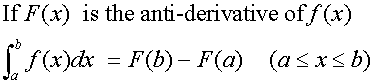
Examples

Evaluate                    

 

            

 

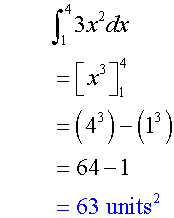
Evaluate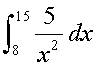    

 

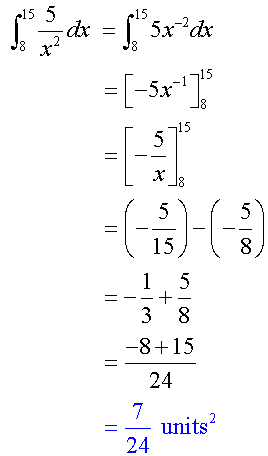
Find the positive value of z :-

 

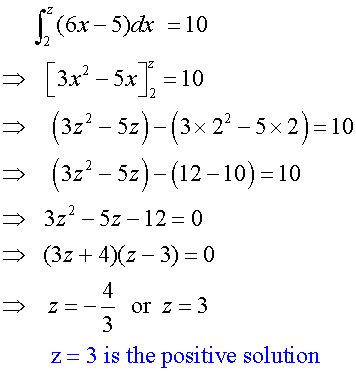
Areas  enclosed by the graph and the x – axis.

 

When calculating the area enclosed by a graph and the x-axis:-

• Always draw a sketch
• Calculate areas above and below x-axis separately
• Ignore negative signs and add.

Example

Calculate the area enclosed by the graph of y = x+2 and the x-axis  for
-6 ≤ x ≤1

 

 

The graph cuts the x-axis at (-2 ,0)

Area below the x-axis =

 

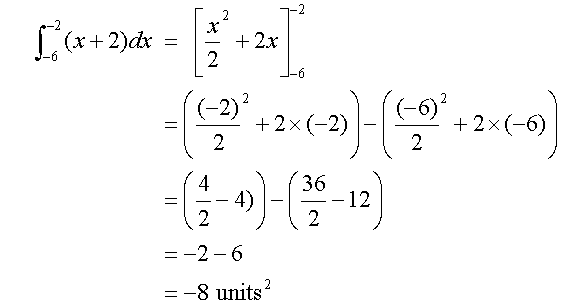
Area above the x-axis =

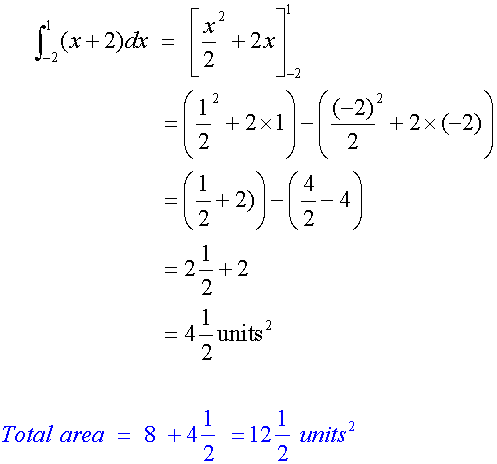
Area between two graphs

 The area between two graphs can be found by subtracting the area between the lower graph and the x-axis from the area between the upper graph and the x-axis.

Example

Calculate the area shaded between the graphs y= x+2 and y = x² .

 

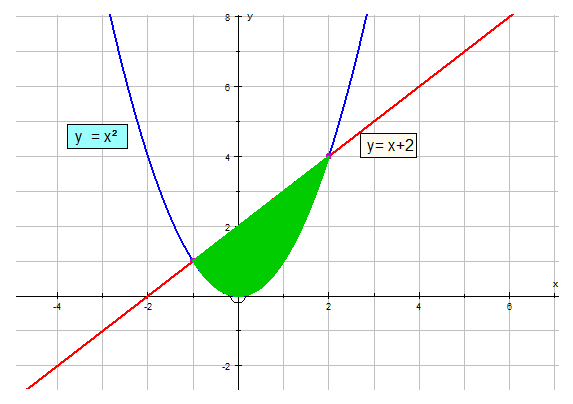
The graphs intersect  at (-1 ,1) and (2,4).

 

Area between upper curve and x- axis

 

 

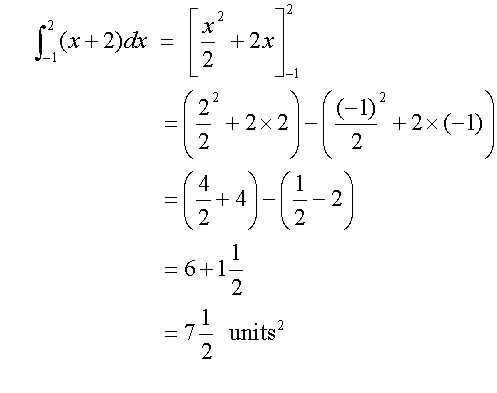
Area between lower curve and x- axis

 

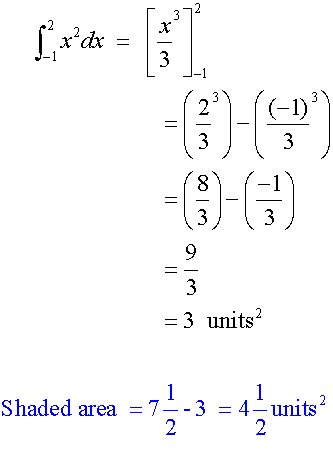
Altogether:

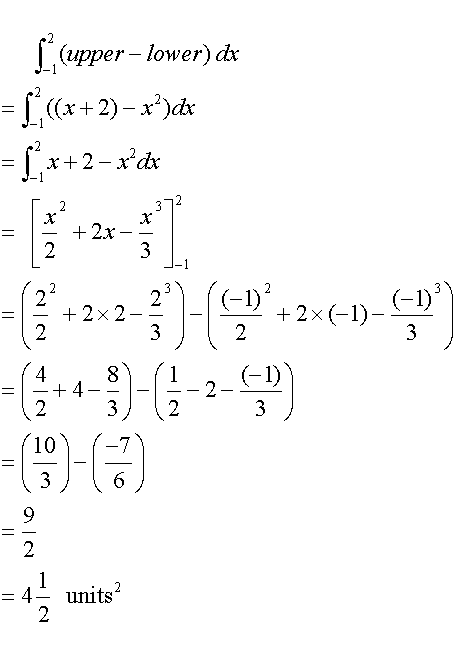
Formula for Area between two graphs

 

 

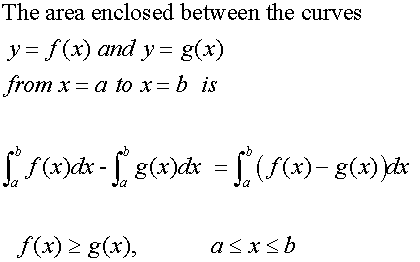
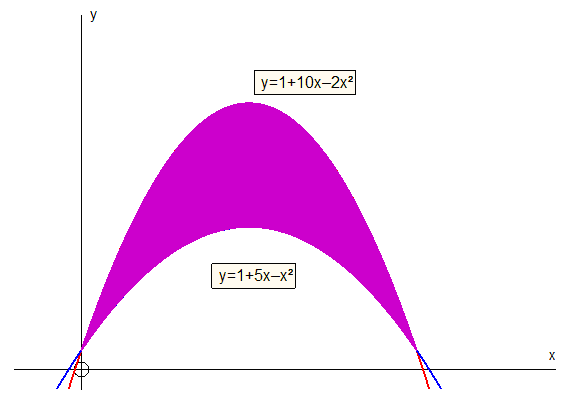
Example

Calculate the shaded area enclosed between the parabolas with equations

y = 1 + 10x – 2x² and y = 1 + 5x – x². (Higher 2002 , p2)