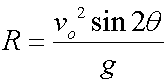Projectile Motion

This applies to a particle which is launced in the vertical plane with an initial velocity, after which it is subject to free fall acceleration.

It is assumed that air has no effect on the projectile.

In projectile motion, horizontal and vertical motion are independent .

The horizontal motion will have zero acceleration.

The vertical motion will have constant downward acceleration, g.

 

A cannon ball is fired from a cannon with an initial velocity Vo m/s²

 

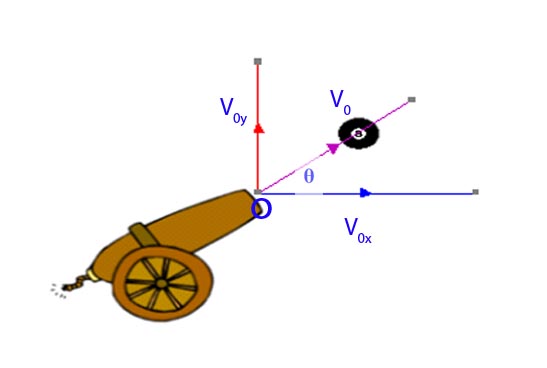
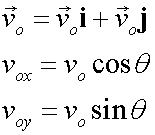
The position vector and velocity vector of the cannon ball will change during the flight, but the ball will experience constant downwards acceleration and no horizontal acceleration.

 

At any given time, the horizontal displacement (x - x₀) can be found using

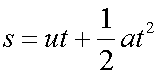
so

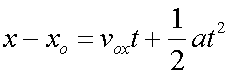
but there is no horizontal acceleration,

so

and

 

Likewise, the vertical displacement (y - y₀) can be found using

 

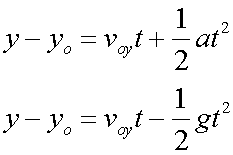
so

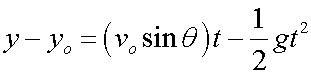
a little rearranging gives

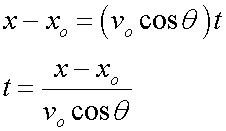
which can be substituted thus:

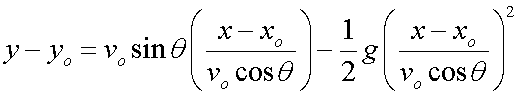
Using the initial conditions,

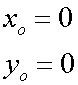
so

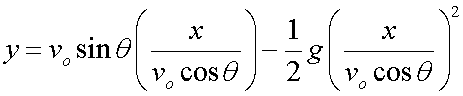
which gives

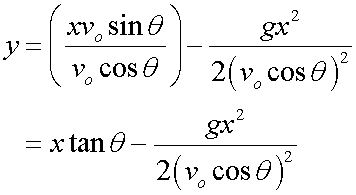
This is the equation of the trajectory of projectile.

 

The horizontal range

The range , R, is the horizontal distance travelled by the projectile when it returns to its launch height.

Since the original launch height is y_o=0,

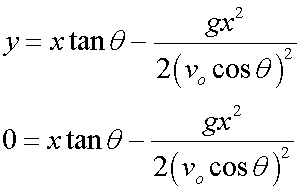
so

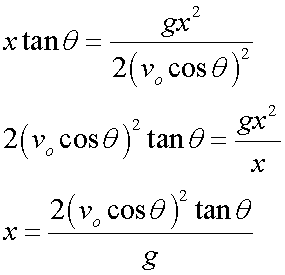
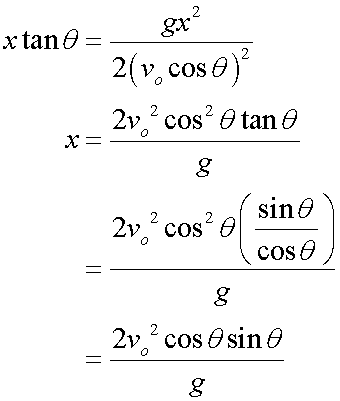
but

so

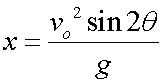
but

so

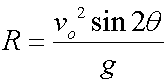
Since the maximum occurs when Sin2θ = 0, the horizontal range is maximum when the projectile is launced at 45 degrees.

 

Alternative proof of the horizontal range equation.

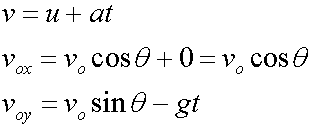
Taking the horizontal direction:

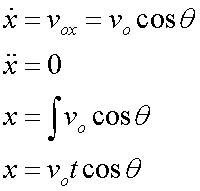
and

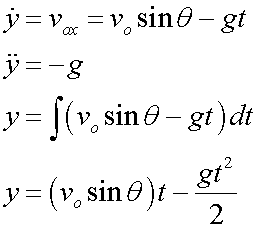
Range occurs when y = 0

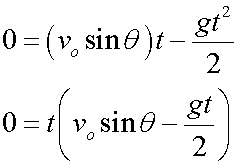
so t = 0 or

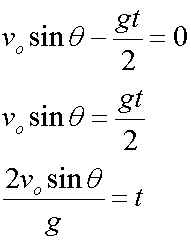
The range is

and

so

so

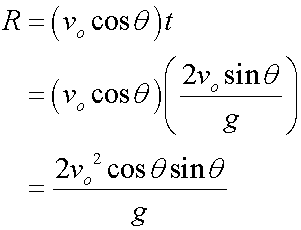
but

so