Translating graphs of functions

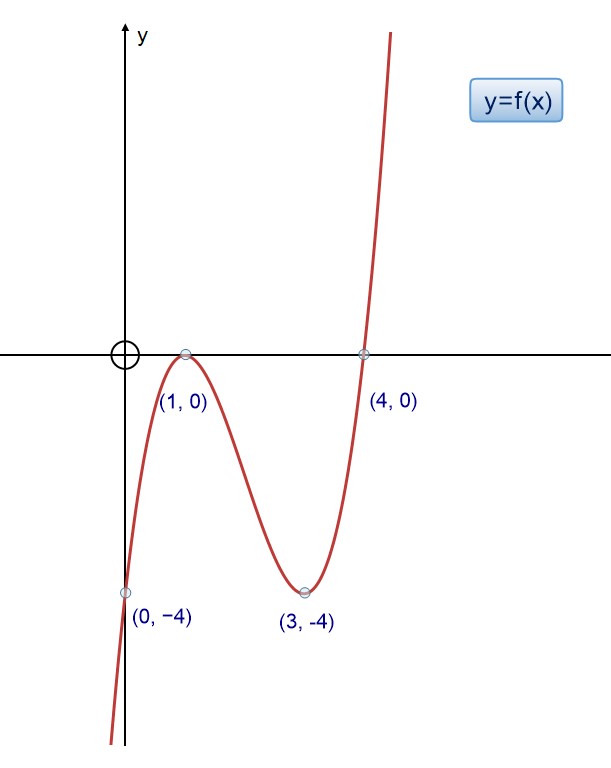
 The following examples all use this graph as the given y=f(x)

Reflection in the  x- axis  gives y=-f(x)

This has the effect of making the y co-ordinate the negative of whatever it was.

Example

 

 

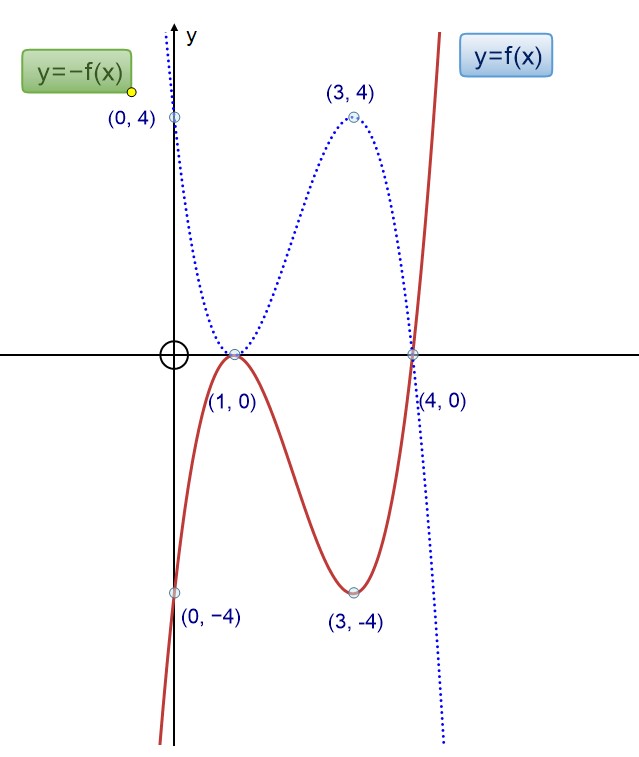
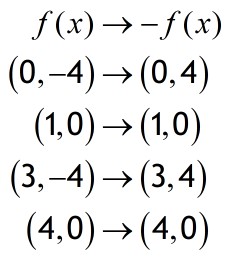
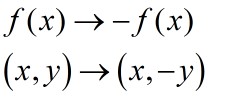
Note that the x co-ordinate is untouched.

 

Reflection  in the  y- axis gives y=f(-x)

This has the effect of making the x co-ordinate the negative of whatever it was.

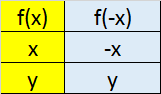
Example

 

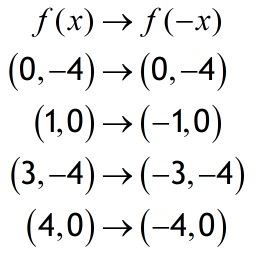
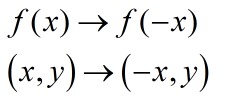
Note that the y co-ordinate is untouched.

 

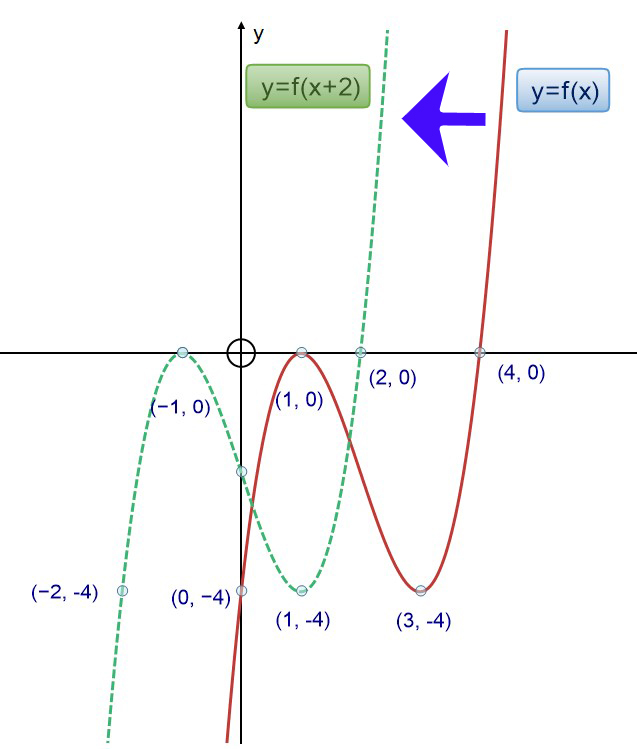
Translate in the x direction to get y=f(x±c)

This has the effect of shifting the entire graph horizontally left or right.

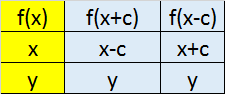
Remember to go the opposite way to the sign,
so for (x - c) go right c spaces

 

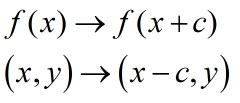
and for (x + c) go left c spaces.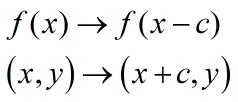

Note that the y co-ordinate is untouched.

Example

 

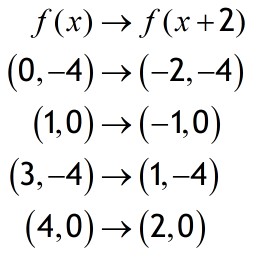
Example

 

 

 

 

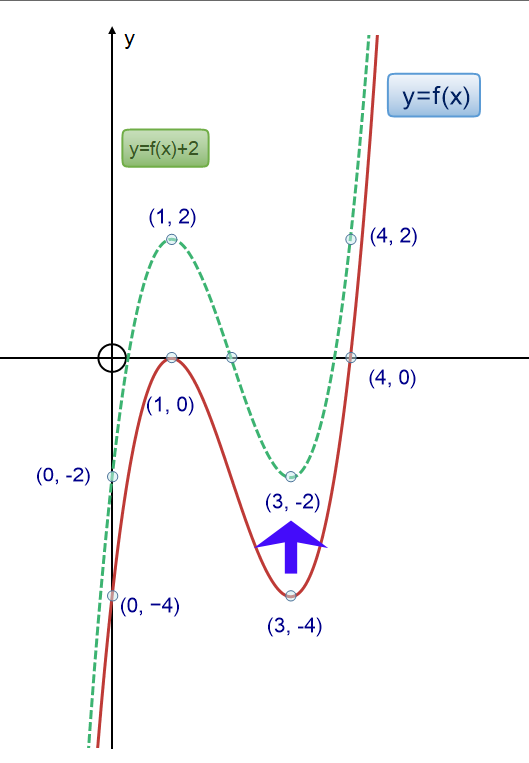
Translate in the y direction to get y=f(x) ± d

This has the effect of shifting the entire graph vertically up or down.

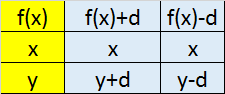
If y=f(x) + d go up d spaces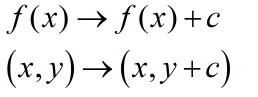

y=f(x) - d go down d spaces.

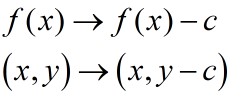
Note that the x co-ordinate is untouched.

Example

 

 

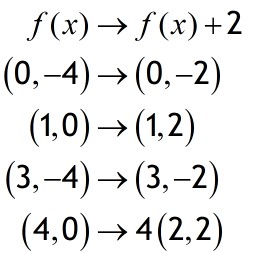
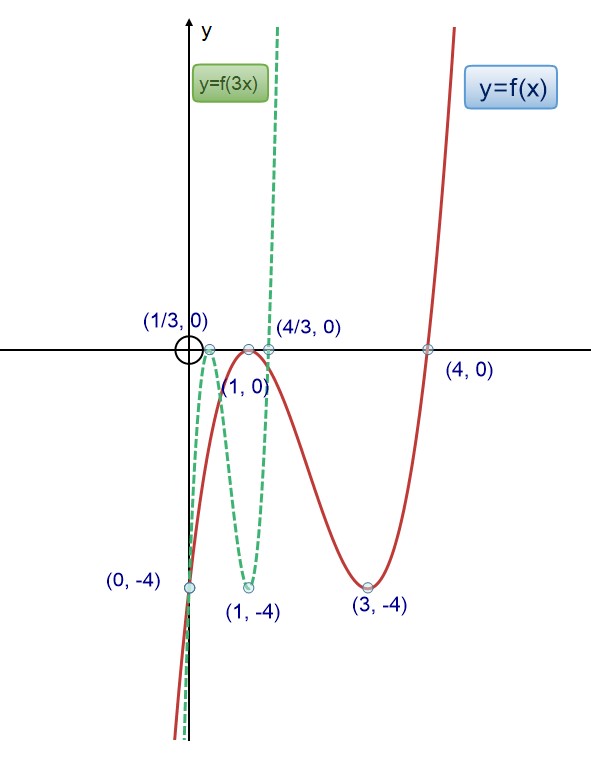
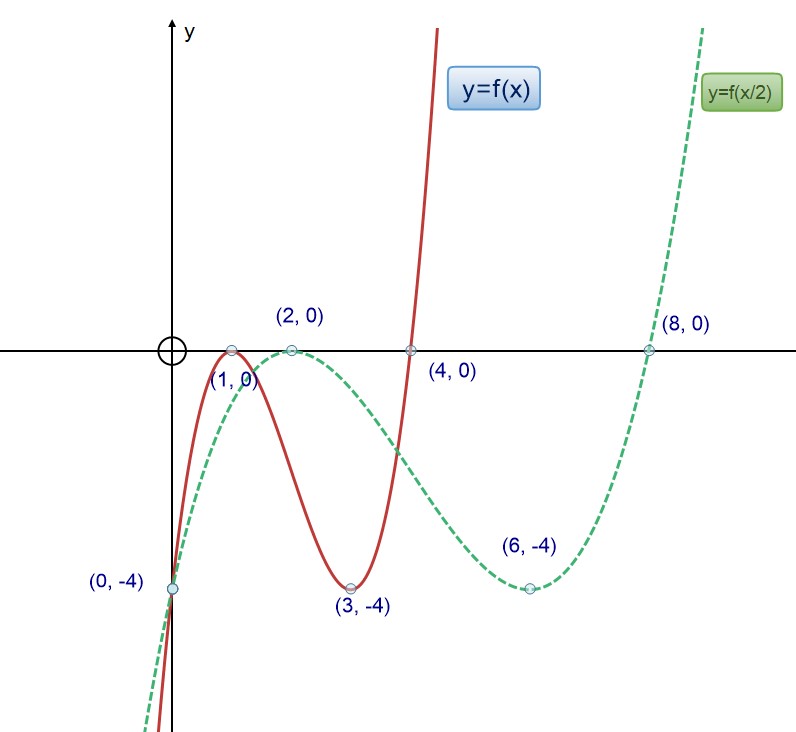
Scale in the x direction to get y=f(bx) or y=f(x/b)

This has the effect of squashing the graph horizontally when b > 1 and stretching it horizontally when b< 1.

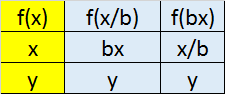
If y = f(bx) divide the x cordinate by b.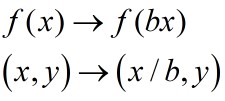

 

If y=(x/b) multiply the x co-ordinate by b.

 

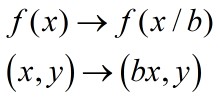
Note that the y co-ordinate is untouched.

Example

 

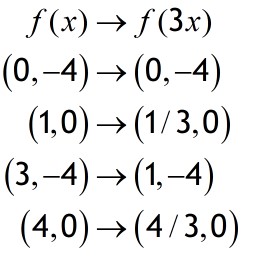
Example

 

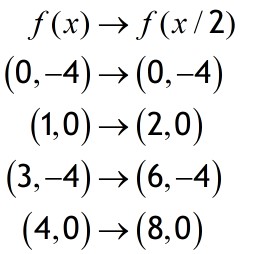
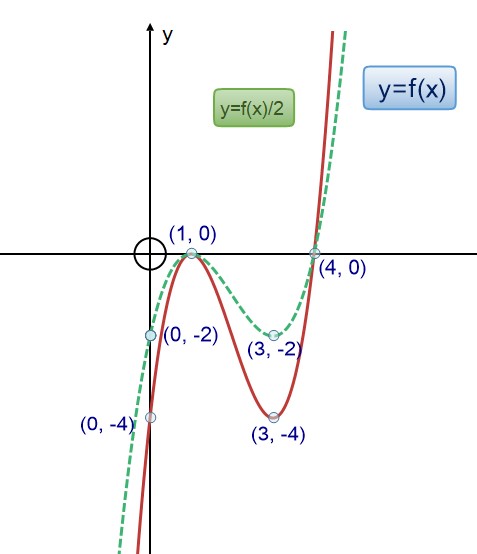
Scale in the y direction to get y=af(x) or y=f(x)/a

This has the effect of stretching the graph vertically when a > 1 and squashing it vertically when a < 1.

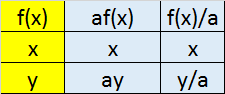
If y = af(x) multiply the y cordinate by a.

 

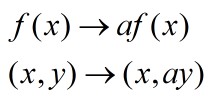
If y = (x/a) divide the y co-ordinate by a.

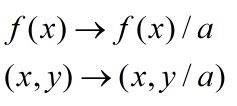
Note that the x co-ordinate is untouched.

 

Example

 

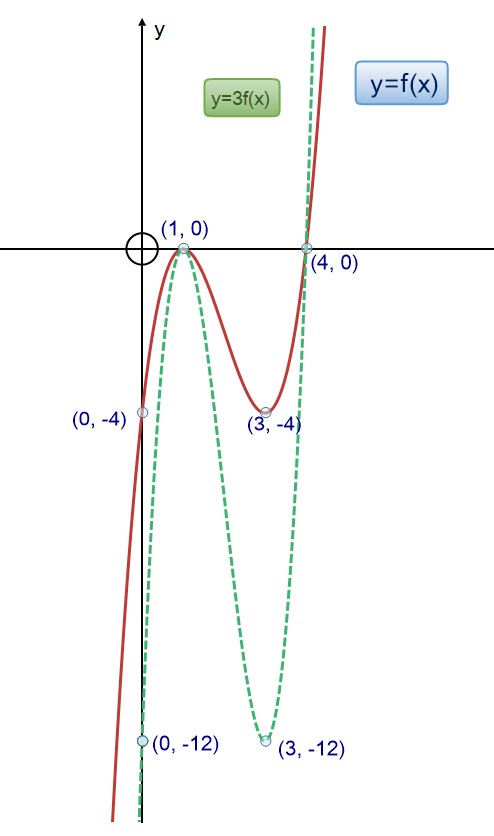
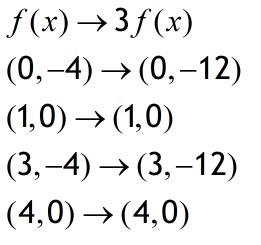
Example

 

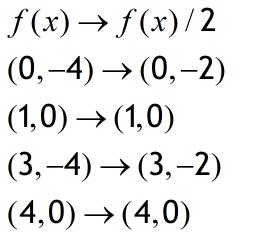
Putting it all together

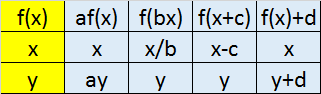
Apply in order c , b , a and finally d

so

1. Shift horizontally C units
2. Squeeze horizontally b units
3. Stretch vertically a units
4. translate vertically d units

 

Example

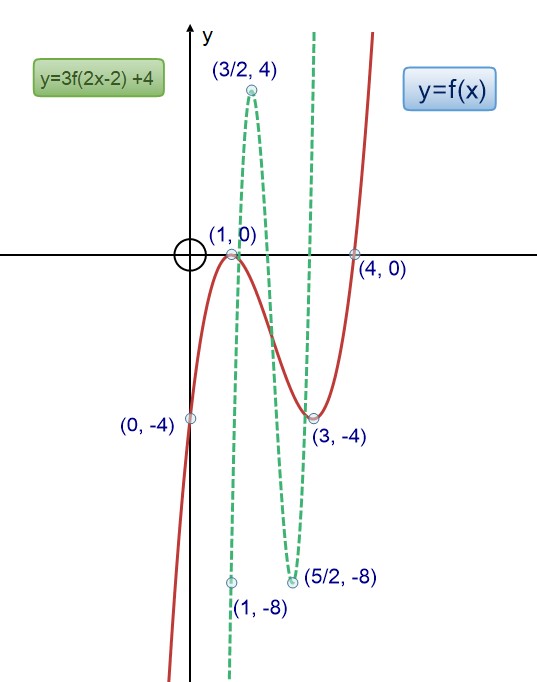
Given y = f(x) as above , draw the graph y = 3f(2x-2) +4

 

Comparing the graph with the general form

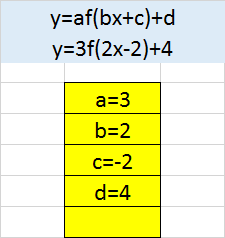
Order of translations

1. c = -2 , so shift graph right 2 units
2. b = 2 , so divide x co-ords by 2
3. a = 3 , so multiply the y co-ordinates by 3
4. d= 4 , so shift the whole graph up 4 spaces

Taking point ( 0 , - 4)

 

Point ( 1,0)

 

Point (3 , - 4)

 

 

 

 

 

 

Working backwards

Given a translated function,

work backwards to get the original y = f(x)

Instead of applying in order c , b , a ,d
apply in order d, a, b, c but backwards

1. translate vertically d units
2. Stretch vertically a units
3. Squeeze horizontally b units
4. Shift horizontally C units

Example

The points (0 , -3 ) and ( 1, 6 ) lie on the graph with equation
y = 1/2f(3x + 2 ) -2 .

Find their corresponding original co-ordinates on the graph y = f(x)

 

 

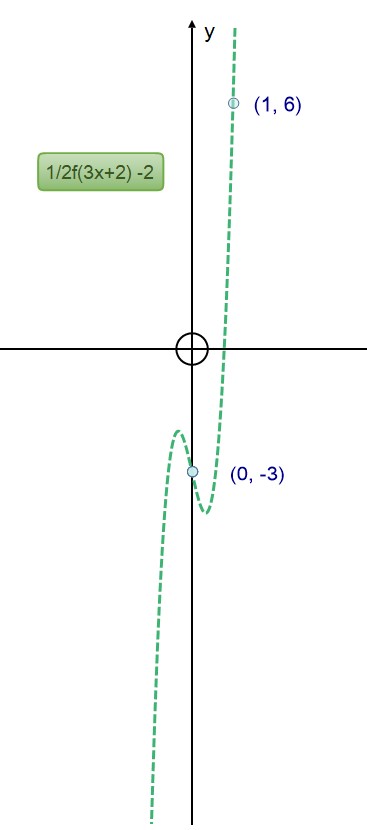
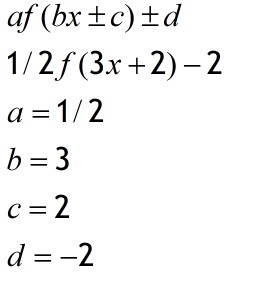
Point (0 , - 3)

 

Point (1 ,6)

 

The original point (5 , 16 ) has been translated to ( 1, 6)

and original point ( 2 ,-2) has been translated to ( 0 , -3 )

 

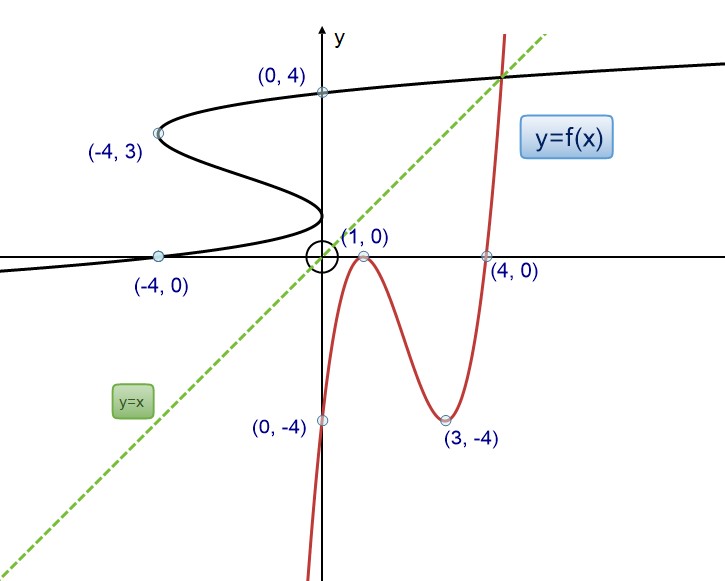
Reflect in the line y=x to get the inverse,

        if it exists

Note that the values of the x and y co-ordinates are swapped, since y = x

Example

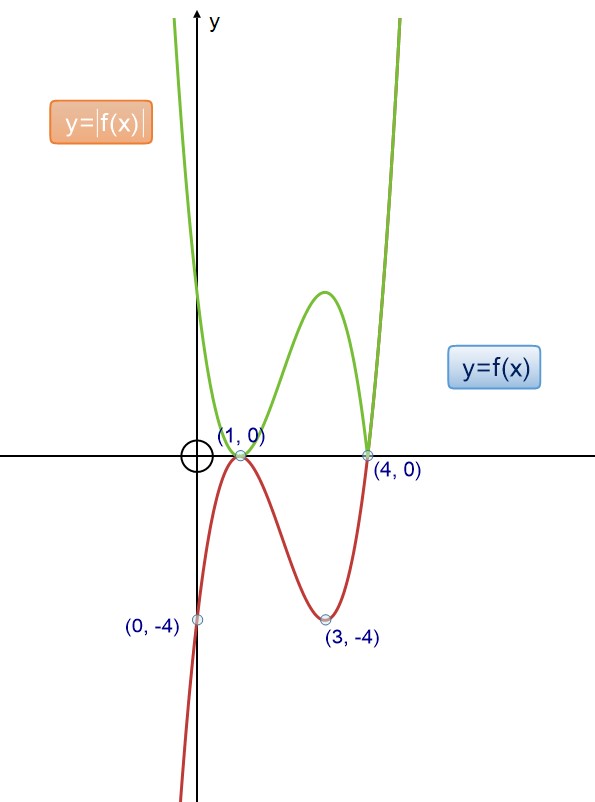
Keep it all positive

y=│f(x)│

The entire graph is above the y-axis

Example