The Division Algorithm

For all positive integers a  and b,
where b ≠ 0,

   

 

Example

Use the division algorithm to find
the quotient and remainder when
a = 158 and b = 17

 

The Euclidean Algorithm

This uses the division algorithm to:-

• find the greatest common divisor (gcd)

[ aka  highest common factor (hcf)]

 

• find the lowest common multiple (lcm) of two numbers

      

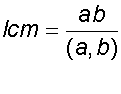
• reduce a fraction to its simplest form

(just divide top and bottom by the gcd)

• find  relatively prime (coprime) integers

These occur when the gcd (a,b) = 1

• Solve  equations of the form

     gcd (a,b) =ax +by

 

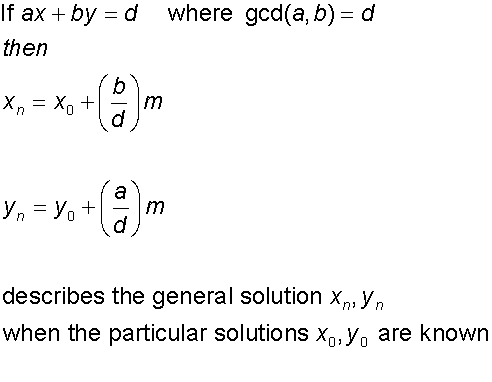
Example

Find the gcd of  135 and 1780

 

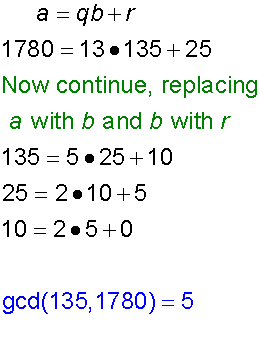
Example

Find the lcm of  135 and 1780

 

Example

Reduce the fraction 1480/128600 to
its simplest form

 

Example

Show that  34 and 111 are co prime

 

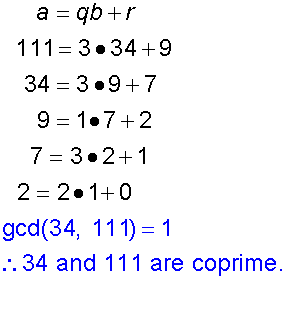
Example

Solve  34x + 111y = 1 ,
where x and y are integers

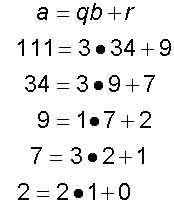
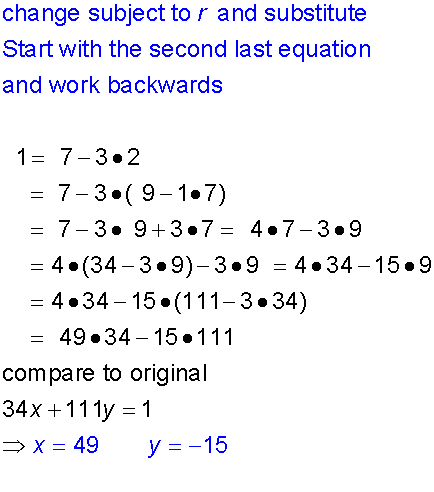
Diophantine Equations

These are of the form

 

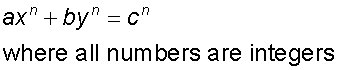
Example

Solve the linear Diophantine Equation
69x +27y = 1332, if it exists

 

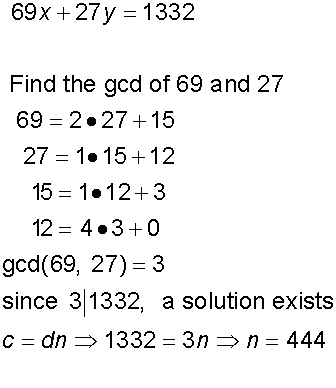
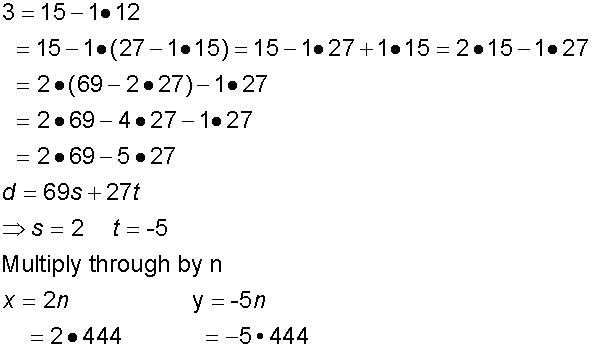
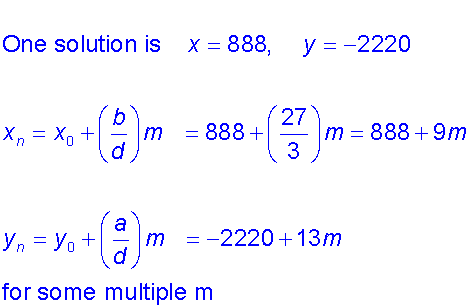
Example

Find the positive integer values of x  and y that satisfy
69x +27y = 1332

 

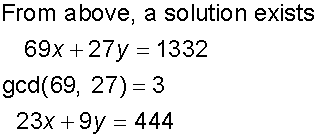
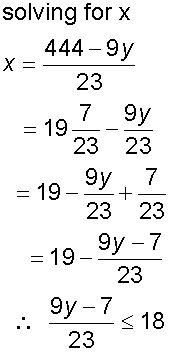
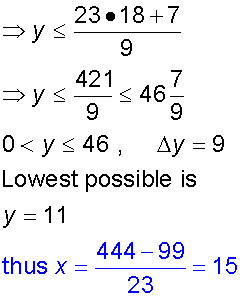
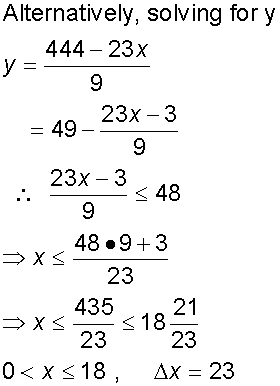
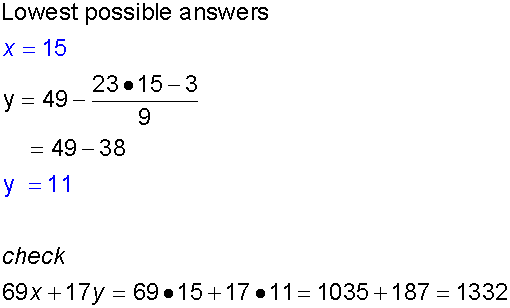
Pythagorean Triples

To find these,
Pick an odd positive number
Divide its square into two integers which are
as close to being equal as is possible

e.g. 7² = 49 = 24 + 25
gives triples  7, 24, 25
                    7² + 24² = 25²

 

Alternatively, pick any even integer n
triples are  2n , n²- 1 and n² + 1
e.g. picking 8 gives  16, 63 and 65 
Indeed 16² + 63² = 65²

 

Fermat’s LastTheorem

Number Bases

To convert a number into a different base,
use the Division Algorithm , taking b as the
 required base.

Example

Convert 36 into  binary 

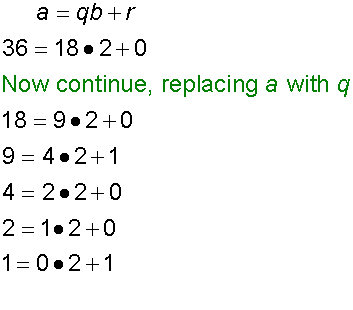
Example

Convert 36 into hexadecimal

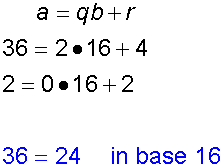
Example

Convert 503793 into hexadecimal
( Remember that hexadecimal uses letters)