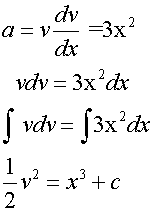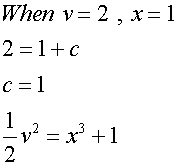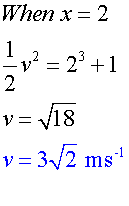Applications of Differential Equations

Differential equations are dynamic, involving instantaneous rates of change.

 

 

• Rocket Science

     

Example

A toy rocket ,consisting of casing and fuel,
is launched at time t=0.
The initial total mass of the rocket is m_o.
The fuel burns such that the mass of the rocket
satisfies the equation

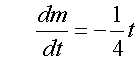
 Given that the mass of the casing =1/2 m_o,
for how long does the rocket’s fuel burn ?

 

 

  

 

 

 

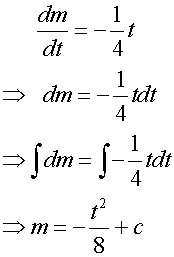
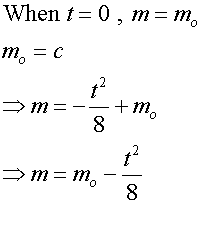
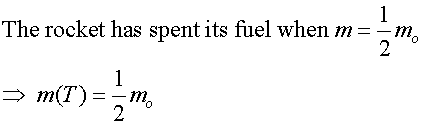
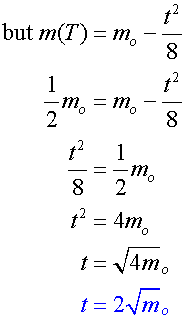
• Newton’s Law of Cooling

The rate at which an object cools is
proportional to the difference between its
temperature and that of its surroundings.

Example

The temperature θ°C of a cup of coffee
t minutes after it was made is given by the
equation

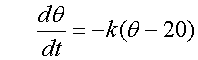
The initial temperature of the drink is 70°C.
5 minutes later, its temperature is 50°C.
When is the temperature 40°C ?

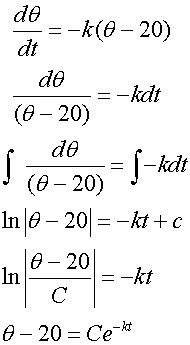
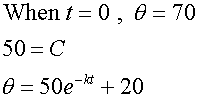
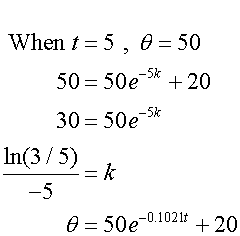
Now for a temperature of40°C

 

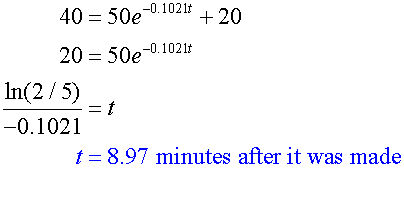
• Growth & Decay

Example

The rate of growth of a population P  is
given by 2P  per day.

Initially, the population is 100.
Find how long it takes for the population to double.

 

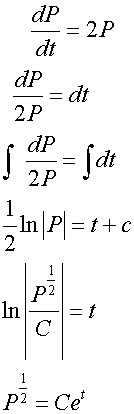
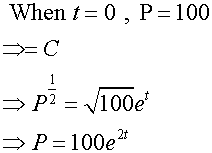
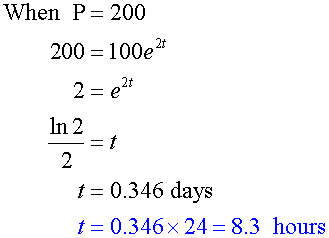
• Kinematics

Example

The acceleration a ms^-2 of a body moving in a straight line
is given as a = 3x² , where x is the distance from the
origin in metres.
When x = 1,  the body has velocity 2 ms^-1
Find the velocity when  x = 2