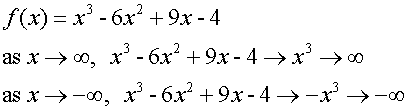Curve Sketching

    To sketch the graph of a function

1. Find the y-intercept by setting the x value to 0. Mark point on graph.
2. Find the x-intercept by setting the y value to 0 Mark point on graph.
3. Find the stationary points by differentiating f(x)
4. Investigate the nature of these stationary points
   • If the gradient is increasing, then decreasing, the turning point is a maximum.
   • If the gradient is decreasing, then increasing, the turning point is a minimum.
   • If gradient is decreasing, then decreasing again or
     increasing and increasing again, the turning point
     is a point of inflection
5. Mark points on graph and lightly sketch shape of tp .
6. Investigate the behaviour of the curve
   • For the upper and lower ends of any closed interval.
     Or
   • For ∞ and -∞
7. Join up the curve.

Example

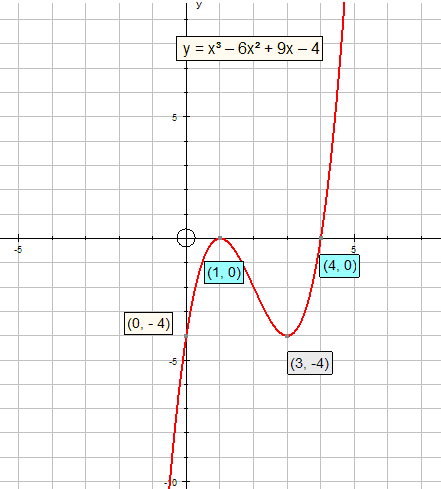
Sketch the graph of the function  f(x) = x³ – 6x² +9x - 4

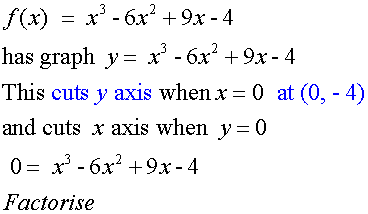
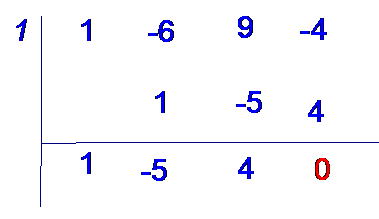
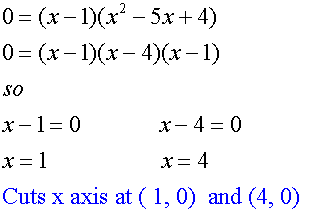
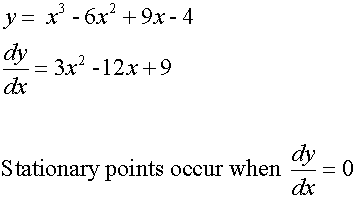
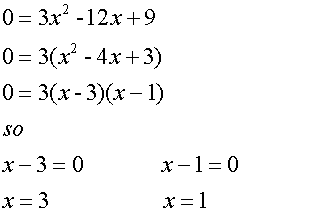
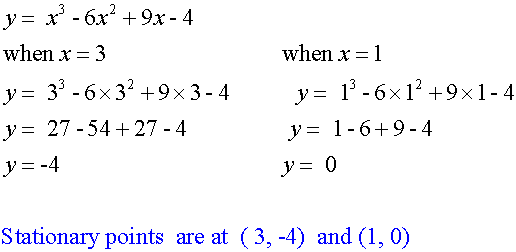
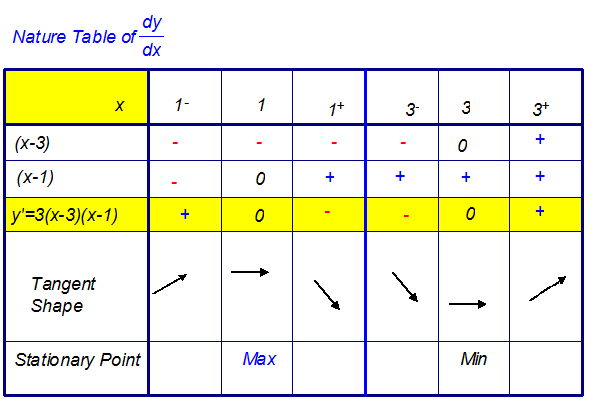
   Hence ( 1, 0) is a maximum  and   ( 3 , -4) is a minimum

This is an open interval, since no restrictions have been placed.

© Alexander Forrest