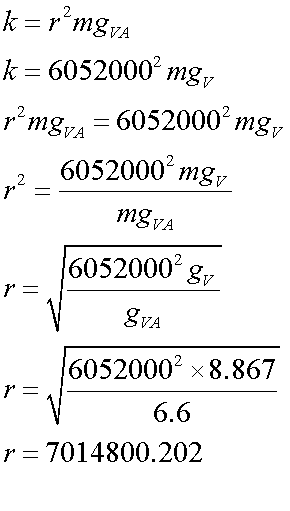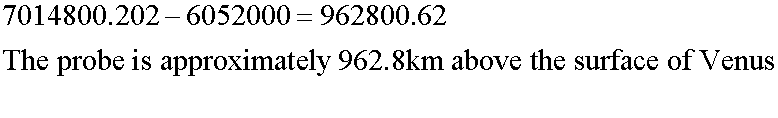Motion in a circle

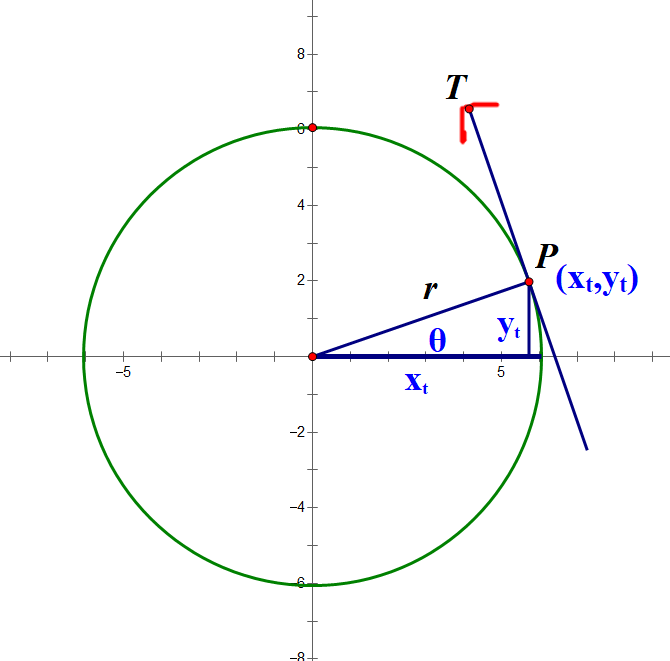
A point, P, is located on a circle with radius r.

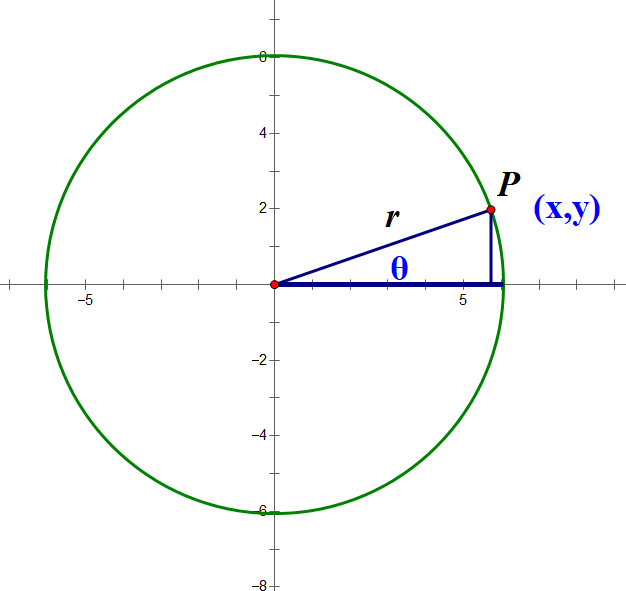
P has co-ordinates (x,y)

where

 

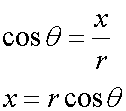
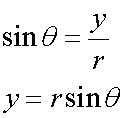
The point is set in motion in an anticlockwise direction.

Its position at time t seconds is

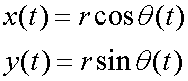
or

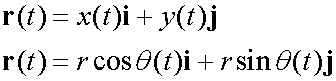
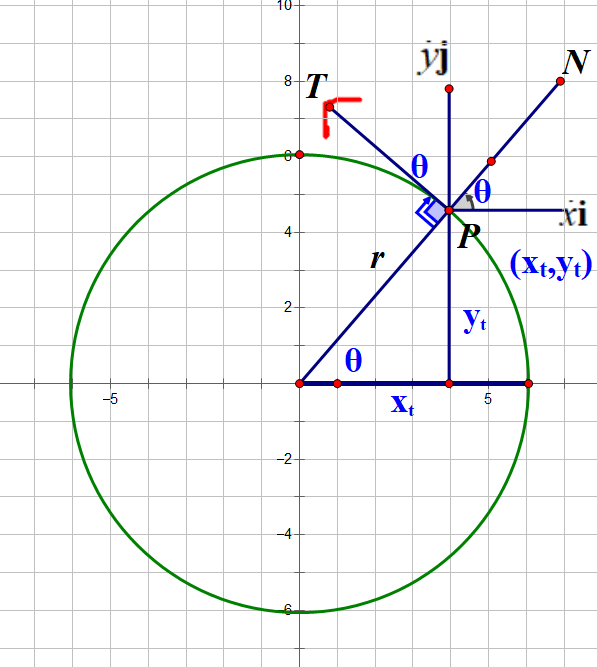
where i and j are unit vectors in the positive x and y axes and θ is the anticlockwise angle between the point and the x axis.

The length of the radius is not dependant upon the time, since the point is moving around a circle.

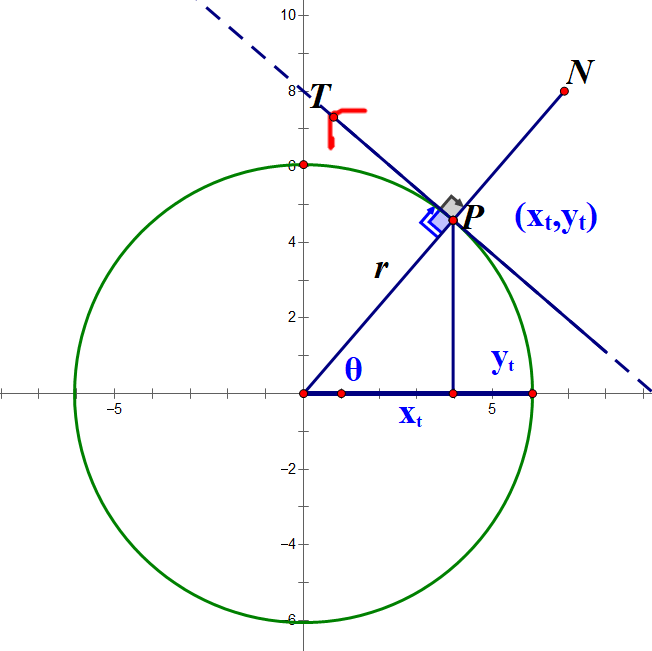
PT gives the direction of travel, or traverse direction of the particle. This is tangential to the circle .

PN is the direction radially outwards, or radial,from the centre of the circle.

The angle between PN and PT is 90°.

Since the particle is moving, the velocity vector of the radial is found :

so

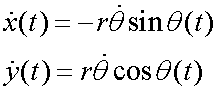
(Don't forget the chain rule!)

so

 

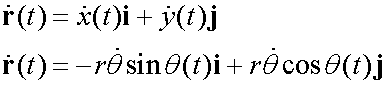
Trig refresher - if required

 

 

 

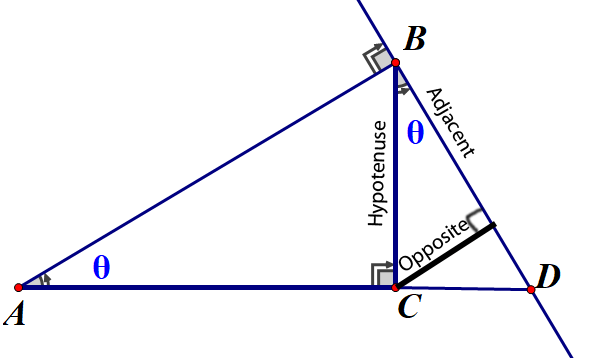
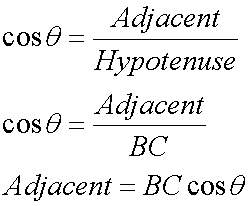
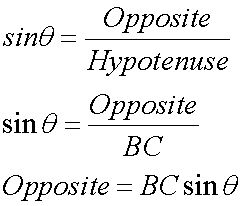
Breaking down into components:

Radial

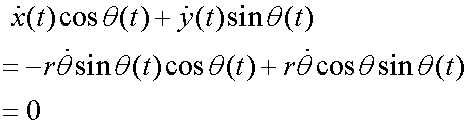
There is no radial component of velocity.

 

Transverse

 

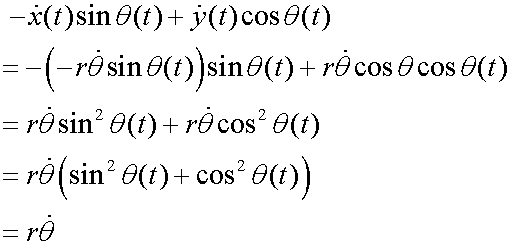
For acceleration,

 

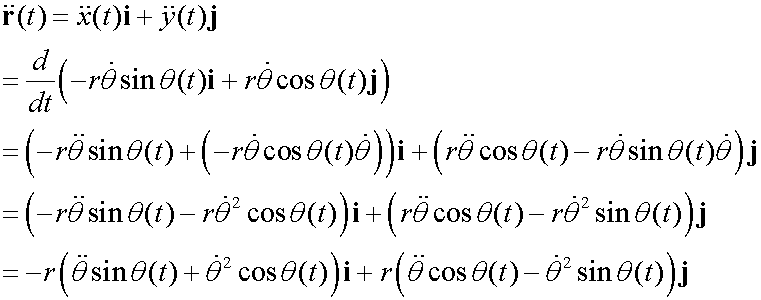
so

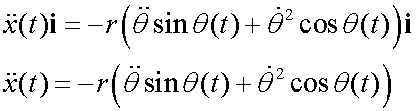
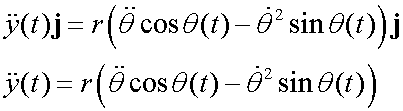
Breaking down into components:

Radial

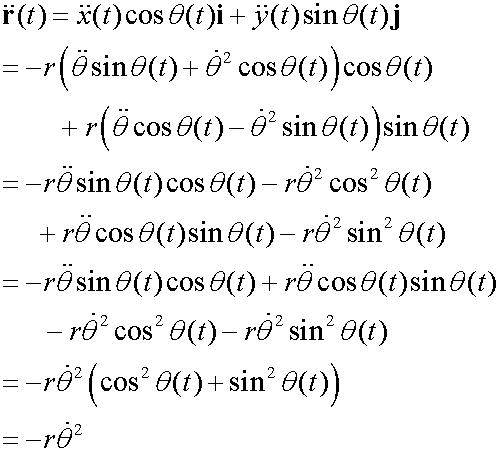
The negative value shows that radial acceleration is towards the centre.

Transverse

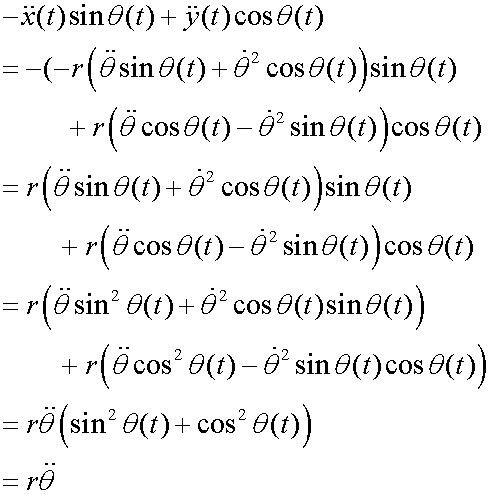
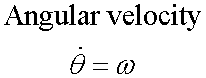
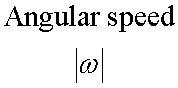
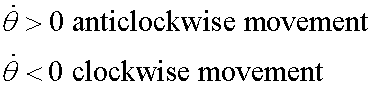
The transverse velocity component

can be referred to as the velocity, since the radial component is zero.

This leads to

and

 

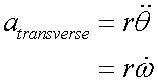
Centripetal acceleration

This is acceleration towards the the center of the circle.

 

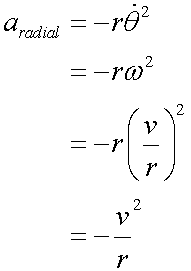
so

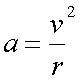
is the equation for centripetal acceleration.

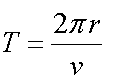
is the period of revolution of the motion: the time taken for one complete revolution.

Uniform circular motion

A particle moving in a circular path must be subject to forces - due to Newton's First Law.

There is no transverse acceleration, but Newton's Second Law shows that there is a force directed towards the circle's centre:

An aircraft is banking .

 

Applying a force diagram:

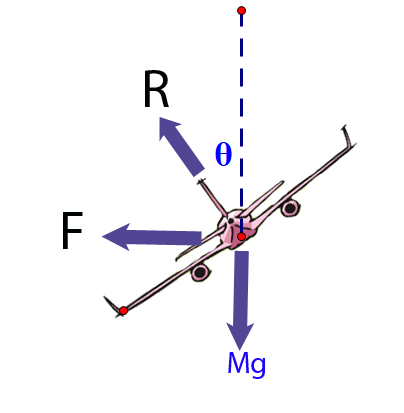
Here, the normal reaction R represents the lift acting on the aircraft.

Examining the horizontal component:

Applying Newton's 2nd Law:

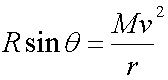
Where v is the aircraft's true airspeed , M its mass and θ its angle of bank. The radius of turn is r.

 

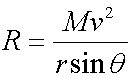
Now looking at the vertical component:

so

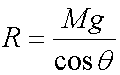
Equating these

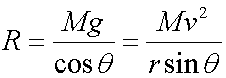
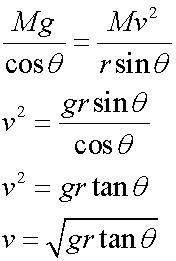
also

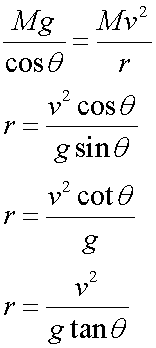
The radius of the turn is proportional to the square of the true airspeed.

Banked Motion

A car is driving at a constant velocity around a banked race track.

 

The car experiences centripetal acceleration, so has a horizontal centripetal force:

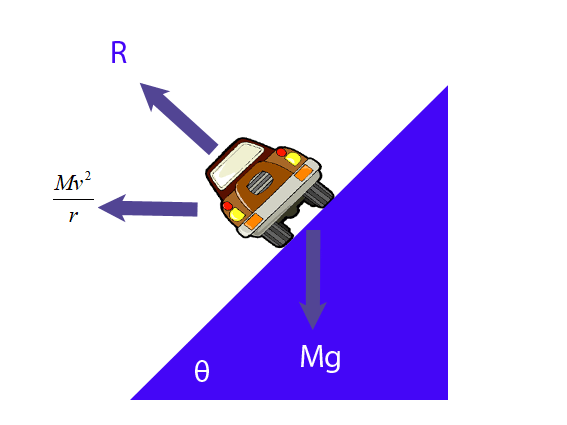
Drawing a force diagram gives

 

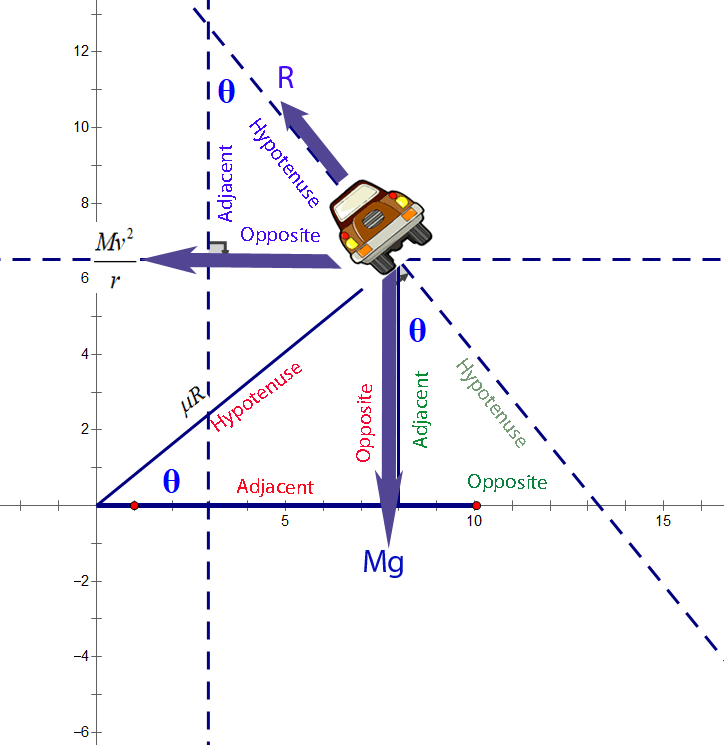
If there is no tendency to slip, then there is no frictional force between the tyres and the road.

Resolving horizontally

 

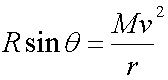
Resolving vertically,

Equating gives the angle of inclination of the bank :

 

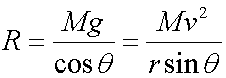
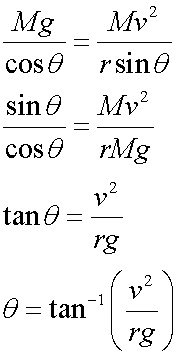
If there is a tendency to slip, then there is a frictional force between the tyres and the road.

Resolving horizontally

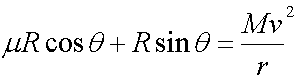
Resolving vertically,

Rearranging these

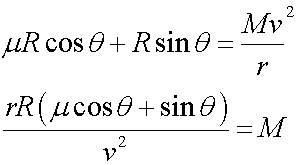
and

 

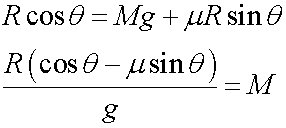
so

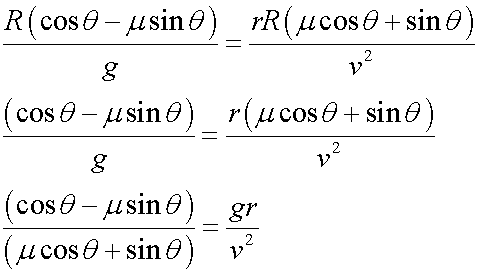
so

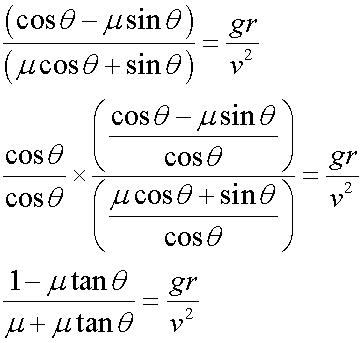
giving

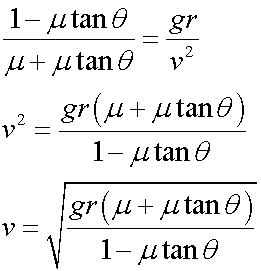
and

 

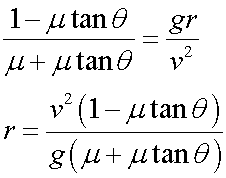
Conical Pendulum

In the diagram below, a bob of mass m Kg is suspended from point A by a light inextensible string of length L. The bob is set to rotate with a constant speed in a circular motion of radius r about a point which is h m vertically below A, so that the string traces out a cone.

 

 

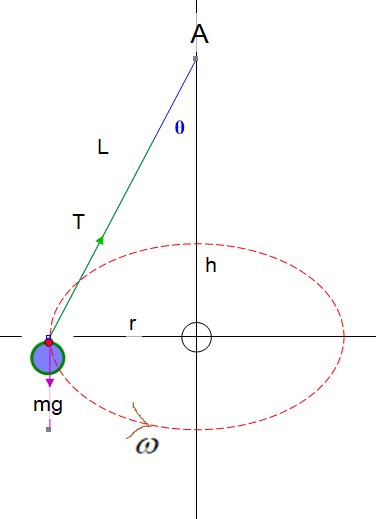
The tension in the string, T, splits into horizontal and vertical components.

The horizontal component is radial:

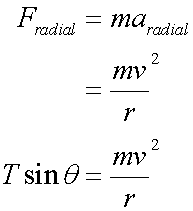
or

 

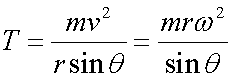
The vertical component:

has no acceleration, so is equal in magnitude but opposite in direction to mg.

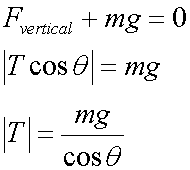
and

 

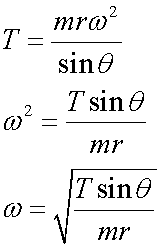
Example

A mass of 300g is attached to a light inextensible string of length 75 cm which is attached to point A. The mass is set to rotate with a constant speed in a circular motion of radius 60 cm about a point which is vertically below A.

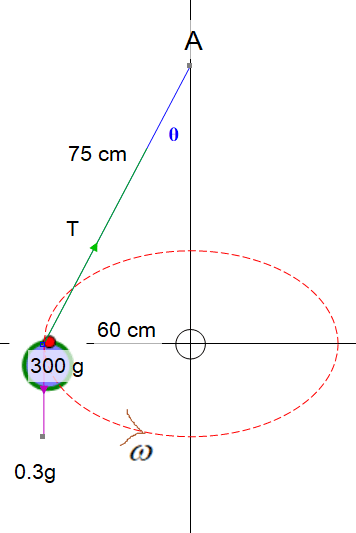
Calculate the tension,T, in the string and the angular speed ,ω.

 

 

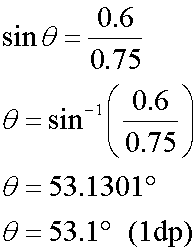
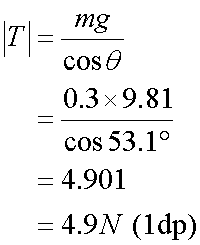
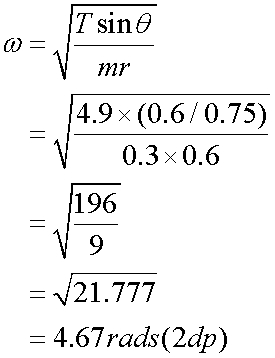
Newton's Inverse Square Law of Gravitation

 

Sir Isaac Newton realised that there was an inverse square relationship between the gravitational effect of a body and the distance from it.

 

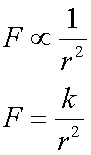
The force between two masses separated by a distance, r, is

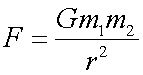
where G is the gravitational constant,

 

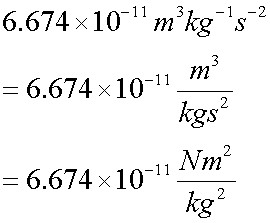
Gravitation near Earth's surface

Let M = mass of the Earth

The gravitational force from Earth on a particle of mass m , located a distance of r metres from the Earth's centre is given by

 

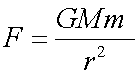
The particle will accelerate towards Earth with acceleration due to gravity, called gravitational acceleration.

 

so

 

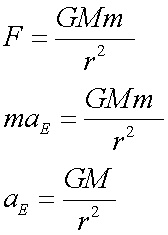
and

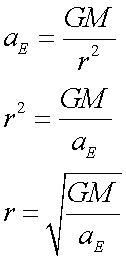
Since the force is attractive, it points backwards towards the source, so a can be replaced by g.

Example

A probe is in a circular orbit above Venus, and experiences acceleration due to gravity at 6.6 m/s².

Venus has a radius of 6052 km and has acceleration due to gravity on the surface of 8.867 m/s².

How high above the surface of Venus is the probe ?

 

Solution

On the surface of Venus

 

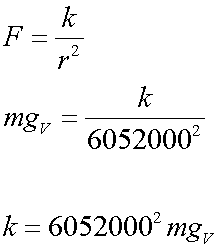
At an altitude above Venus,

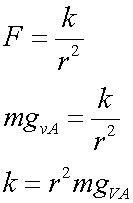
Equating for k