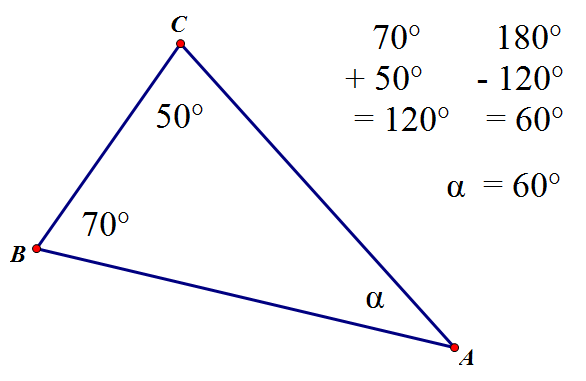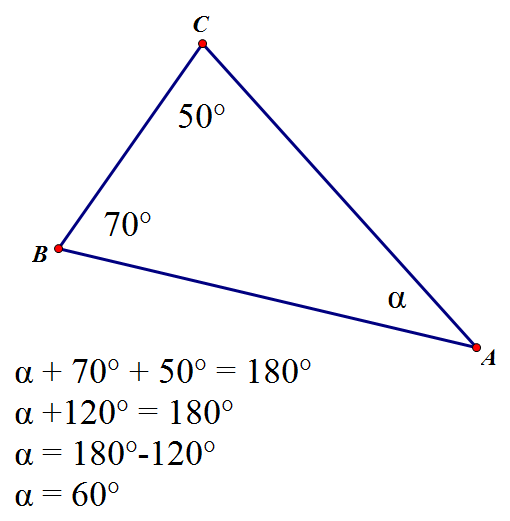Naming angles
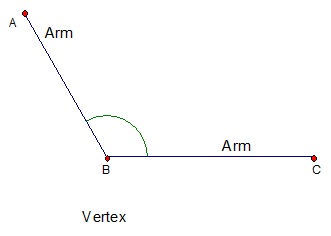
Angles have two arms and a vertex.
B is the vertex of the angle, A and C are arms.
The vertex of an angle is always written as the middle letter.
So angle ABC can be written as:
\( \angle ABC \quad \text{or} \quad \angle CBA \)
Usually, angles are written with a hat on the middle letter:
\( A \hat{B} C \)
Angle types
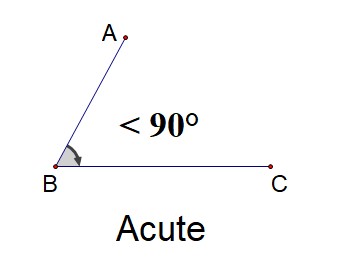
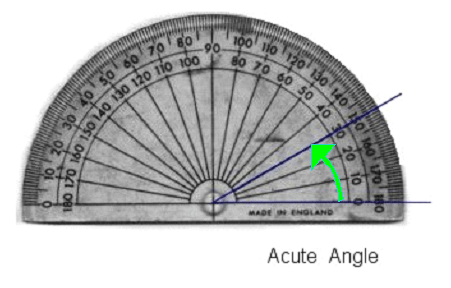
An acute angle lies between \(0^\circ\) and \(90^\circ\).
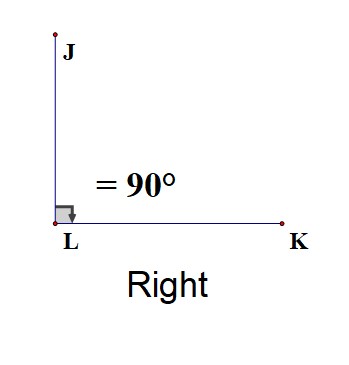
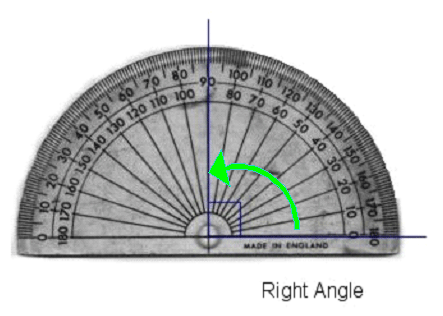
A right angle is exactly \(90^\circ\).
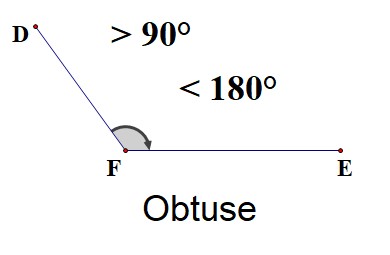
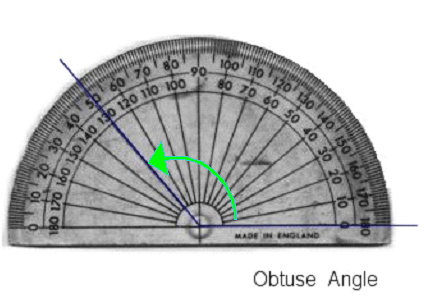
An obtuse angle lies between \(90^\circ\) and \(180^\circ\).
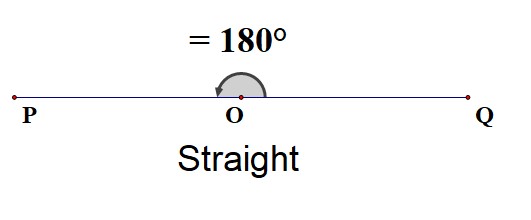
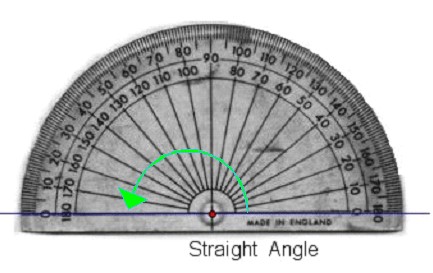
A straightline is \(180^\circ\).
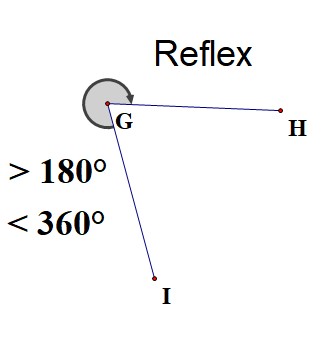
A reflex angle is between \(180^\circ\) and \(360^\circ\).
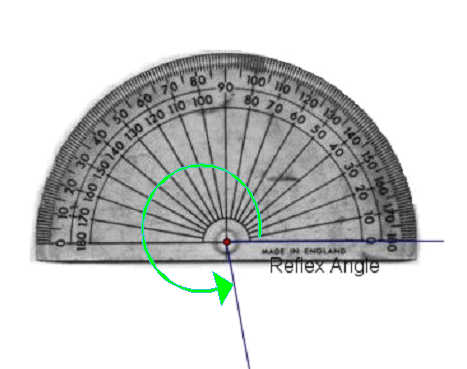
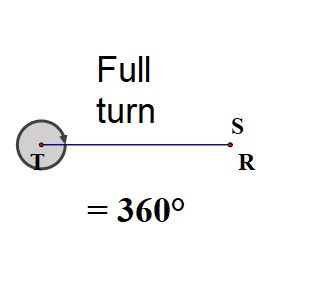
A full turn is \(360^\circ\).
Lots of pupils mix up an angle's name with its type.
Here is a small mnemonic:
Amy is a cute cat.
What is her name? Amy
What type of cat is she? A cute one.

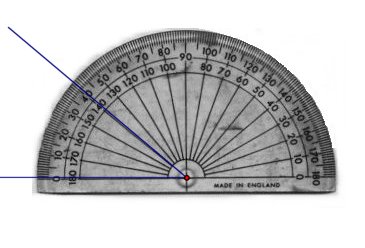
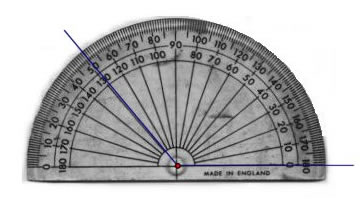
How to use a protractor – measuring angles
- Place the protractor so that its centre point is on the vertex and the \(0^\circ\) line is over one arm.
- Read from the scale that starts at \(0^\circ\).
How to use a protractor – drawing angles
- Draw a line.
- Place the protractor so that its centre is on one endpoint.
- Read from the scale starting at \(0^\circ\).
- Mark the required angle.
- Remove the protractor.
- Join the new point to the endpoint.

Complementary angles
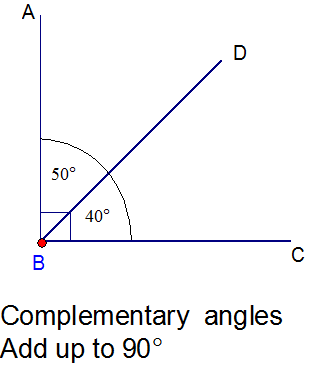
\( a + b = 90^\circ \)
Supplementary angles
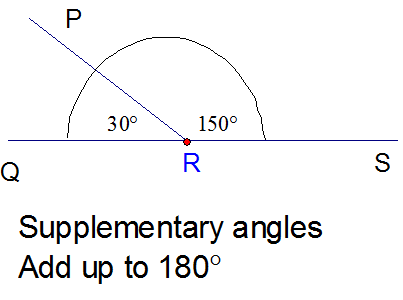
\( a + b = 180^\circ \)
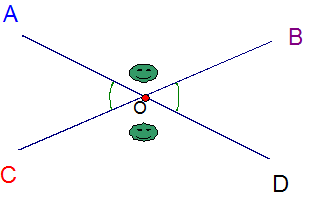
Vertically opposite angles
When two straight lines cross, the angles opposite each other are equal.
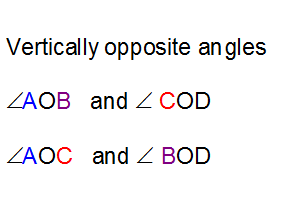
Corresponding angles
Corresponding angles appear in matching corners.
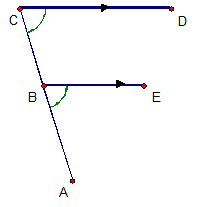
\( \text{Corresponding angles are equal.} \)
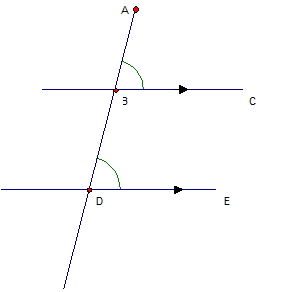
\( a = b \)
Interactive – Corresponding AnglesAlternate angles
Alternate angles lie on opposite sides of the transversal.
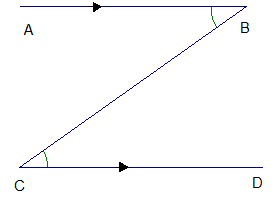
\( \text{Alternate angles are equal.} \)
The angles in a triangle
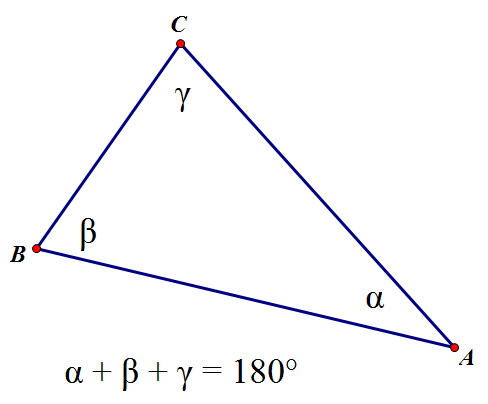
The angles in a triangle add up to \(180^\circ\).
\( a + b + c = 180^\circ \)